Design Considerations

Limit States

Allowable Strength Design

Design Requirement: A structural design is intended to support and/or transmit loads while maintaining safety and utility: don't break. Strength of a structure reflects its ability to resist failure.

Ultimate load ( $ P_u $ ): force when specimen fails (breaks).
Ultimate normal stress ( $ \sigma_u $ ): stress when a specimen fails (breaks).

Ultimate normal stress

$$ \sigma_u = \frac{P_u}{A}\ $$

A structure is safe if its strength exceeds the required strength.

Factor of Safety (FS): Ratio of structural strength to maximum (allowed) applied load ($ P_{all} $).

Maximum allowed applied load.

$$ P_{all} \le \frac{P_u}{FS}\ $$

Similarly,

Maximum allowed applied stress.

$$ \sigma_{all} \le \frac{\sigma_u}{FS}\ $$

Load and Resistance Factor Design

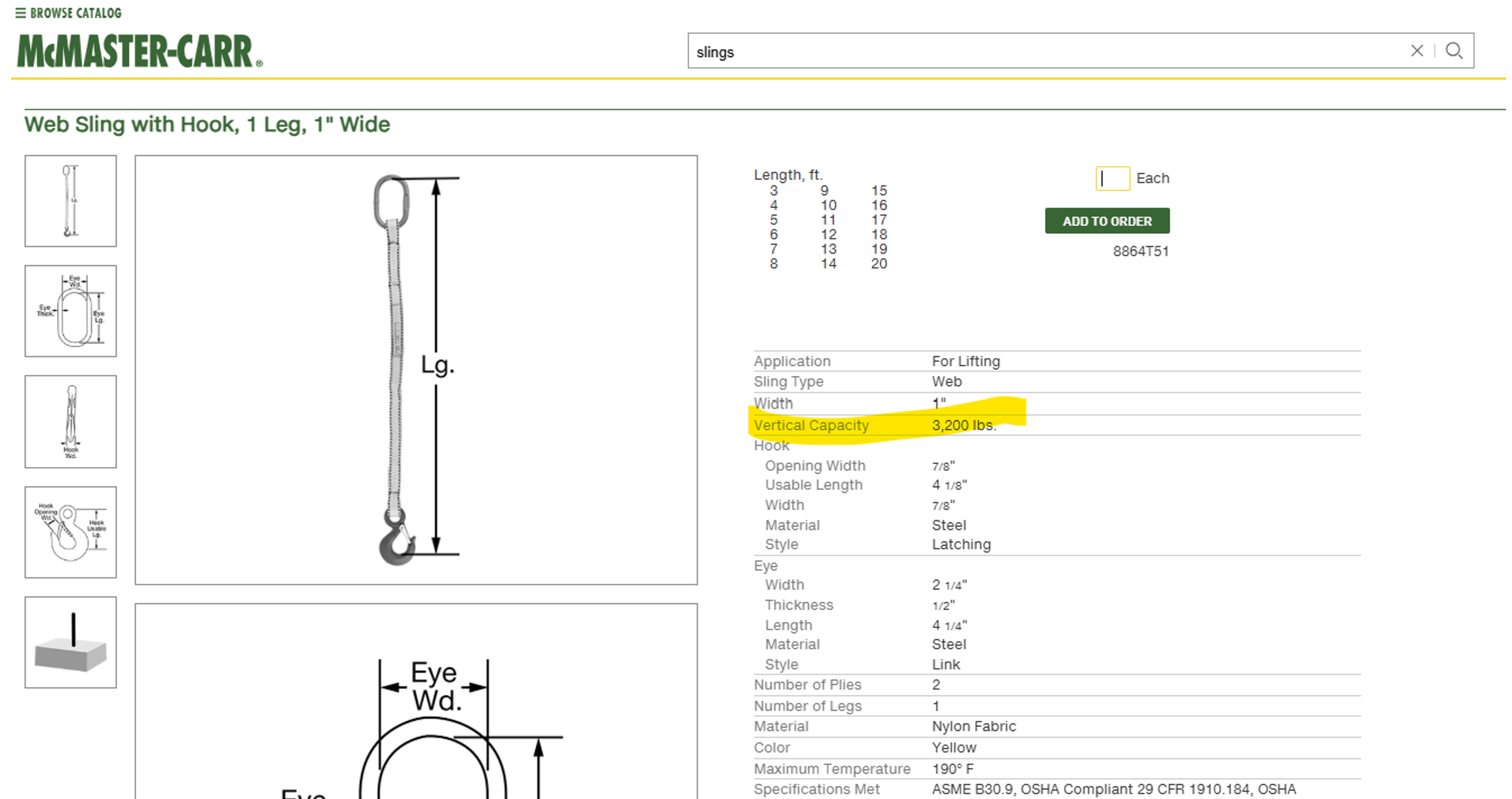
Depending on the industry or application, the acceptability of a design may be interpreted differently. For some applications showing a factor of safety of 4 may be sufficient. For example, a sling used for lifting, such as the one shown below, is specified to have a safety factor of 5 in ASME B30.9.

Web sling

In the civil/structural engineering industry, the variability of loading (wind, seismic, etc.) has been studied extensively. This is also true for various structural capacities in building materials like steel, concrete wood, etc. Given a loading and resistance that are both random variables, a simple “safety factor” does not result in a consistent level of probability of failure across all structures. The structural engineering industry addressed this inconsistency with a different design approach known as Load and Resistance Factor Design (LRFD.)

The intent of LRFD is to ensure a reasonably low probability of failure is met. The probability of failure can be calculated using the statistical distributions of loading and resistance. Finding the probability that loading exceeds capacity is equivalent to integrating the probability density function (PDF) of the loading multiplied by the cumulative distribution function (CDF) of the resistance (capacity). This can be thought of as accumulating the likelihood of all possible instances of loading being relatively high and the capacity being relatively low in order to find a cumulative probability of failure. The example plots shown below assume normal distributions of load and resistance.

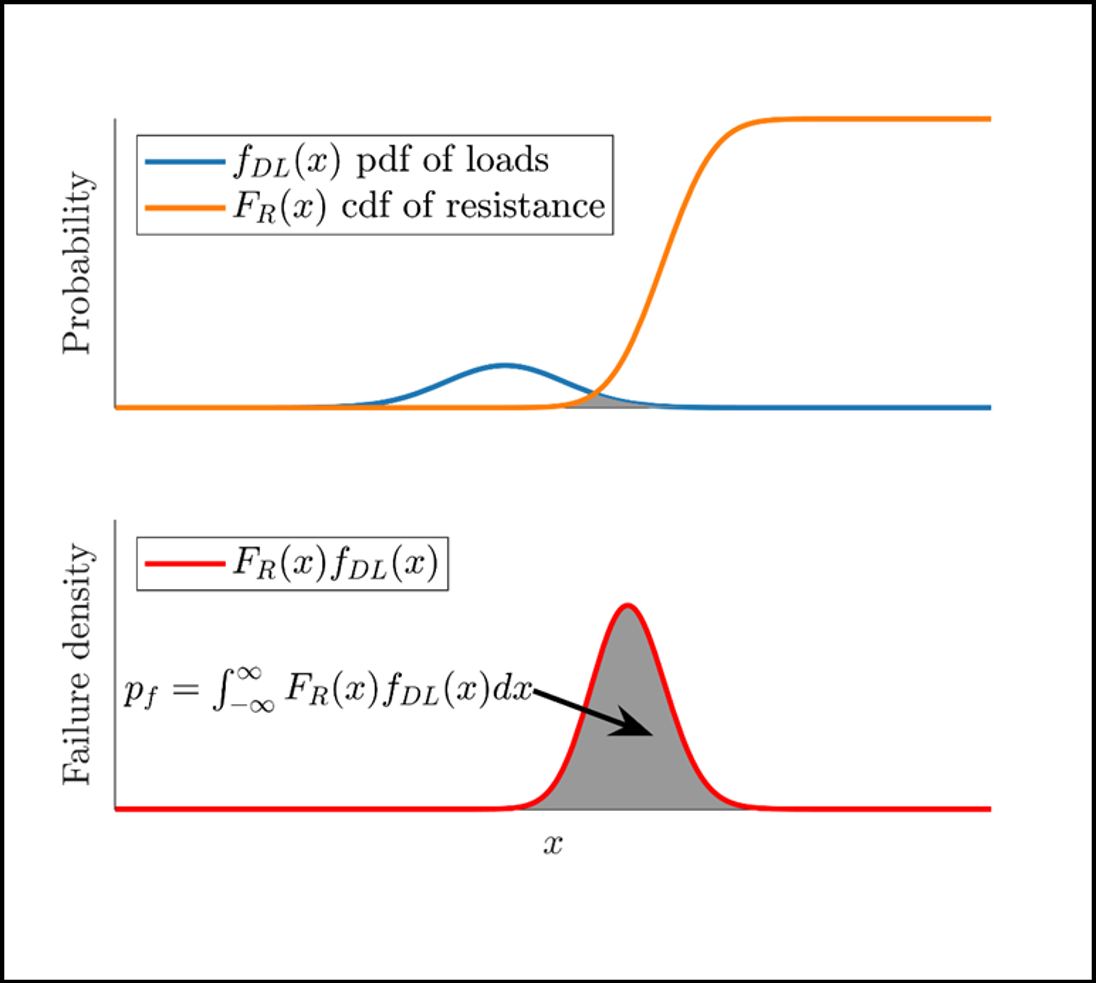
Example of loading probability distribution

For bridge design, both approaches are discussed in AASHTO LRFD and LRFD for Highway Bridge Superstructures Reference Manual Section 1.2.2.