Reference Pages
Mechanical Engineering

    Scroll back to top

    Current page:

    Principle of Superposition

    Deformation

    Superposition: If the displacements are (1) small and (2) linearly related to the force components acting, the displacements caused by the components can be added up:
    Superposition.
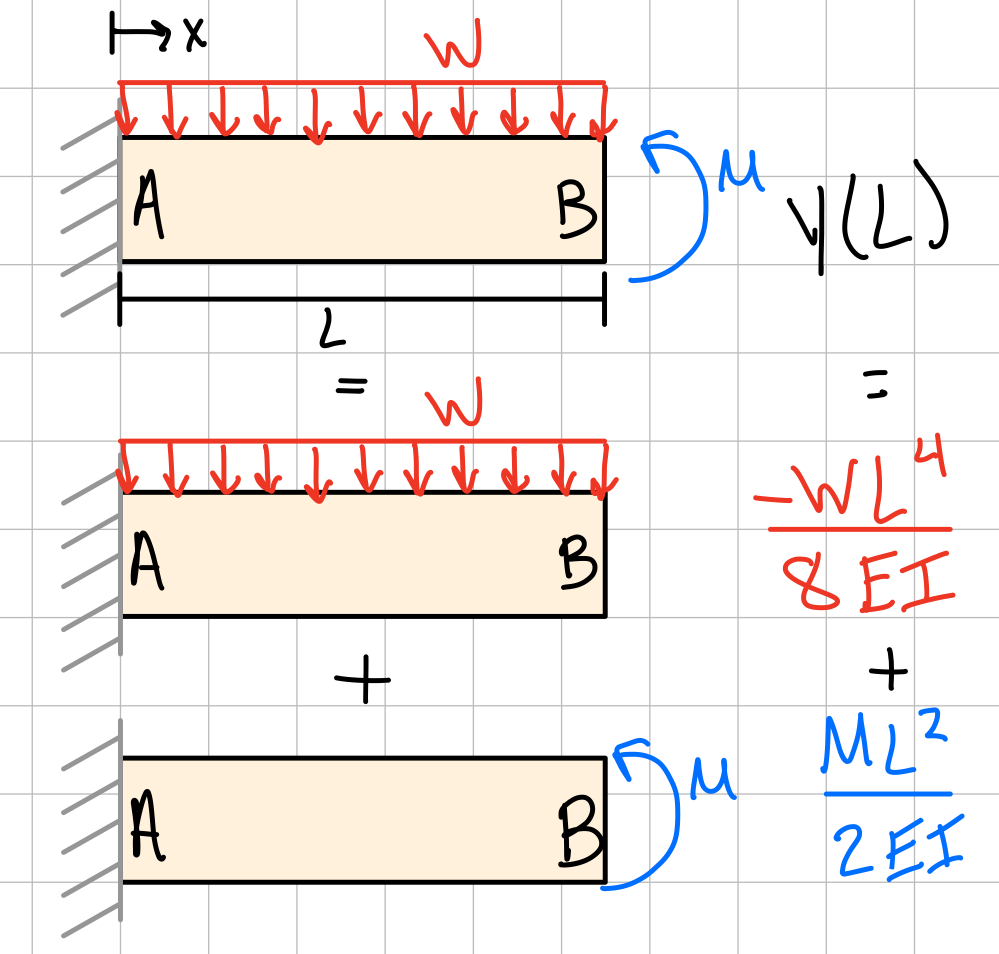
    $$ \delta = \sum_i \delta_i = \sum_i \frac{F_i L_i}{E_i A_i}\ $$
    Superposition can also be applied to beam deflection by adding the deflections from different types of loadings.
    Example: Deflection from a moment and distributed load using superpositon. #dfl-spp

    Stress

    If a loading results in more than one type of stress, the total stress in a cross-section can be calculated by adding the individual stresses together (superposition). A review of the stresses covered in this course is below: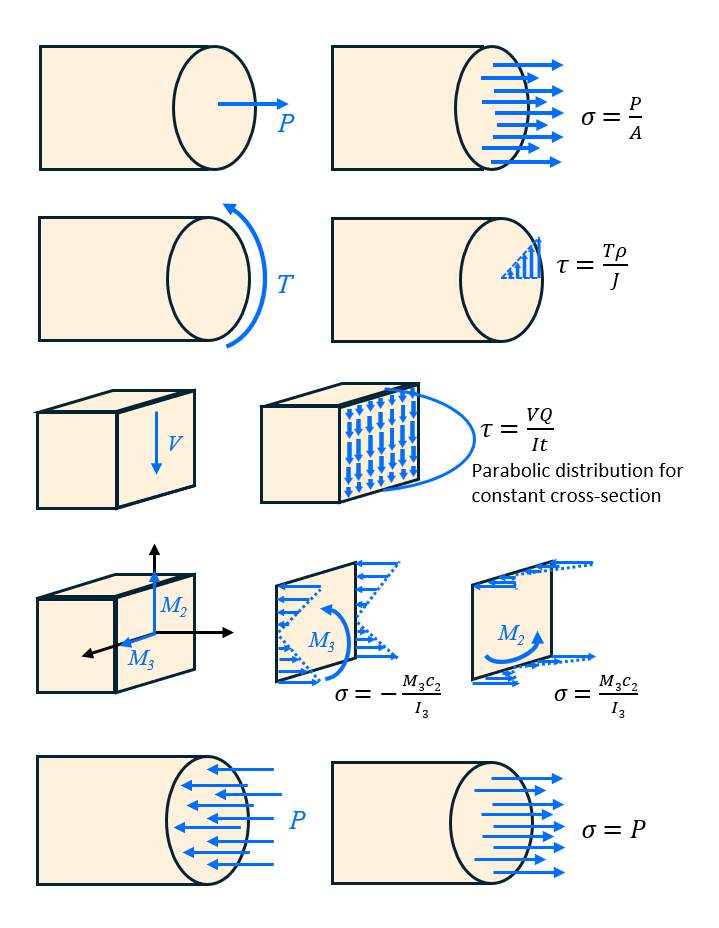
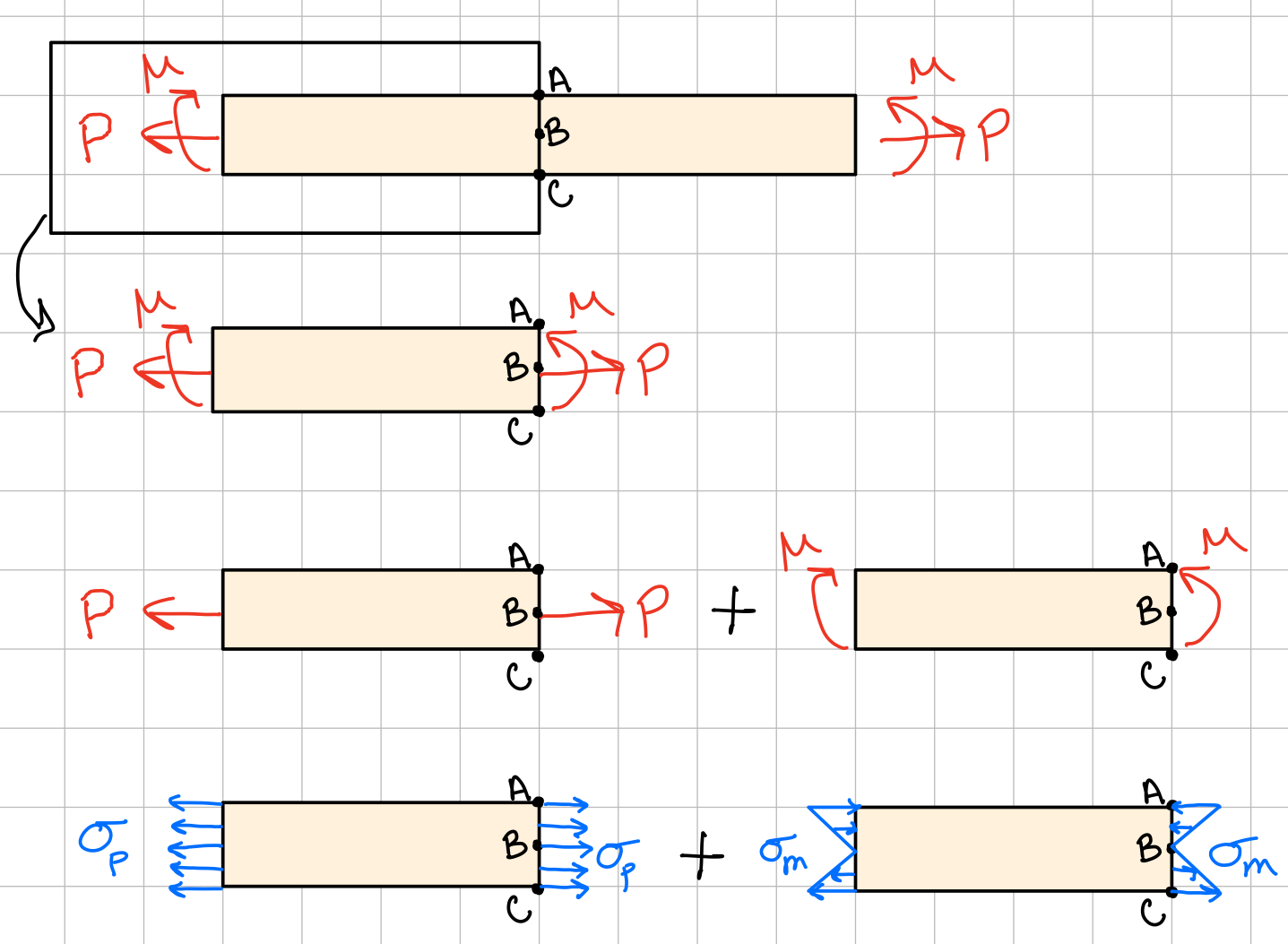
    The goal in combined loading is to determine the stresses at a point in a slender structural member subjected to arbitrary loadings. A cross-section is cut through the point of interest and the internal loading/moments are evaluated at the centroid of the section to maintain equilibrium. This internal system of loading will consist of three force components and three couple vectors (moments). To determine the stress distribution at the point, the principle of superposition is applied.
    Steps:
    1. Cut the beam to find the find internal forces/moments in a section of interest.
    2. Calculate all the stresses acting at a specific point within that section.
    3. Add up like stresses (matching subscripts) to find the total stress state (superposition).