Current page:

Stress-Strain Diagram
- Elastic Behavior
- Plastic Behavior
Other Derived Properties
- Directional Materials
- Poisson's Ratio

Material Properties

Continuum Mechanics Fundamentals

Generally, the state of stress a 3D material can be represented as a second-rank tensor (i.e. a matrix) with $ 3^2 = 9 $ components.

Infinitesimal Stress element

Stress tensor.

$$ \boldsymbol{\sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{bmatrix} \ $$

Using indicial notation, component $ (i, j) $ of this tensor is denoted as $ \sigma_{ij} $. The same can be said for a material strain tensor.

Infinitesimal Strain Element

Strain tensor.

$$ \boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33} \end{bmatrix} \ $$

Using indicial notation, component $ (k, l) $ of this tensor is denoted as $ \varepsilon_{kl} $. Note that both the stress and strain tensors are symmetric, that is $ \sigma_{ij} = \sigma_{ji} $ and $ \varepsilon_{kl} = \varepsilon_{lk} $.

For our purposes, lets bound the discussion of material stress-strain behavior to only the elastic range, that is, deformation is linear proportional applied load. This is Hooke’s law. The relationship between stress and strain is referred to as the constitutive relationship of a material. In the most general case, this relationship is defined as a fourth-rank tensor with $ 3^4=81 $ components. This elasticity tensor, C, relating the stress and strain tensors is shown in indicial notation (rather than a matrix operation).

Hooke's law general form. #mat-hls

$$ \sigma_{ij} = C_{ijkl}\varepsilon_{kl} $$

This is short form representation of a summation, known as indicial notation. Whenever there are repeated indices on the right hand side of an equation, as with k and l above (repeated in $ C_{ij\mathbf{kl}} $ and $ \varepsilon_{\mathbf{kl}} $), these indices represent a summation over three dimensions. So the example can be rewritten as shown below, where $ k\ \in \{1 \ 2 \ 3\} $ and $ l\ \in \{1 \ 2 \ 3\} $.

$$ \sigma_{ij} = \sum_{k=1}^{3}\sum_{l=1}^{3}C_{ijkl}\varepsilon_{kl} $$

Expanding over these two summations yields:

$$ \begin{aligned}\sigma_{ij} = &C_{ij11}\varepsilon_{11} + C_{ij12}\varepsilon_{12} + C_{ij13}\varepsilon_{13} \\ + &C_{ij21}\varepsilon_{21} + C_{ij22}\varepsilon_{22} + C_{ij23}\varepsilon_{23} \ + C_{ij31}\varepsilon_{31} + C_{ij32}\varepsilon_{32} + C_{ij33}\varepsilon_{33}\end{aligned} $$

What this means is there can be as many as 9 components of strain and 9 material coefficients that contribute to each stress component. (You can see the benefit of indicial notation here.)

However, not all 81 components of this tensor are independent, because of symmetry of stress and strain tensors there are only 21 independent components. If the material is assumed to be isotropic (having the same behavior in all directions) this is further reduced to just 2 independent components (for instance, $ E $ Young’s modulus and $ \nu $, Poisson’s ratio). With this simplification, the 3D isotropic elastic material constitutive relation can be simplified.

Voigt notation.

$$ \begin{bmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{33} \\ 2\varepsilon_{23} \\ 2\varepsilon_{13} \\ 2\varepsilon_{12} \end{bmatrix} = \begin{bmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{33} \\ \gamma_{23} \\ \gamma_{13} \\ \gamma_{12} \end{bmatrix} = \frac{1}{E} \begin{bmatrix} 1 & -\nu & -\nu & 0 & 0 & 0 \\ -\nu & 1 & -\nu & 0 & 0 & 0 \\ -\nu & -\nu & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 + 2\nu & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 + 2\nu & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 + 2\nu \end{bmatrix} \begin{bmatrix} \sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \sigma_{23} \\ \sigma_{13} \\ \sigma_{12} \end{bmatrix} $$

Here the engineering shear strains $ \gamma_{23},\gamma_{13},\gamma_{12} $ are introduced. This, along with identification of shear stresses $ \sigma_{23},\sigma_{13},\sigma_{12} $ as $ \tau_{23},\tau_{13},\tau_{12} $ allows for the expression for pure axial stress & strain in one direction to be represented as $ \varepsilon_{11} = \frac{\sigma_{11}}{E} $. Rearranging the terms, relation can be expressed in a more general form.

Simplified Hooke's Law.

$$ \sigma = E\varepsilon $$

Similarly, the expression for pure shear stress & strain can be expressed as $ \gamma_{12} = \frac{\tau_{12}(2+2\nu)}{E} = \frac{\tau_{12}}{G} $. Again, this can be expressed in a more general form.

Simplified shear stress equation.

$$ \tau = \gamma G $$

Extra!

If you want more details on this topic, consider taking a course in continuum mechanics.

Notation Note

Bold symbols, such as $ \boldsymbol{\sigma} $ and $ \boldsymbol{\varepsilon} $, represent tensors rather than scalar quantities.

Additionally, some quantities might be represented with indicial notation. When indices on the right hand side of the equation are repeated, this represents a summation where the index values range from 1 to 3. For example,

$$ \sigma_{ij} = C_{ijkl}\varepsilon_{kl} $$

represents

$$ \sigma_{ij} = \sum_{k=1}^{3}\sum_{l=1}^{3}C_{ijkl}\varepsilon_{kl} $$

This is a shorthand to make writing long summations easier.

Stress-Strain Diagram

A stress-strain diagram is the relationship of normal stress as a function of normal strain. One way to collect these measurement is a uniaxial tension test in which a specimen at a very slow, constant rate (quasi-static). A load $ P $ and distance $ L $ are measured at frequent intervals.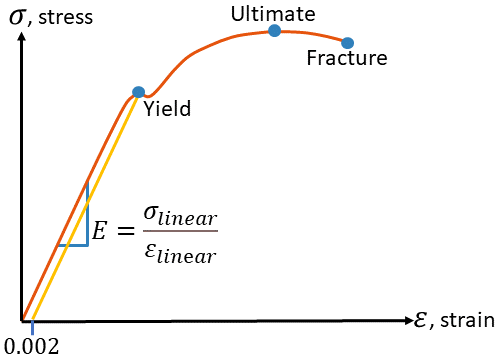

Evaluation of average normal strain, or engineering strain (relative to undeformed length).

$$ \varepsilon = \frac{\delta}{L_0} = \frac{L-L_0}{L_0}\ $$

Evaluation of average normal stress, or engineering stress (relative to undeformed cross section).

$$ \sigma = \frac{P}{A_0}\ $$

Warning: Two stress-strain diagrams for a particular material will be similar, but not identical. #str-stn

Things that effect the material properties include imperfections, different composition, rate or loading, or temperature.

Stress-strain diagram showing key properties

Elastic Behavior

Loading in this region results elastic behavior, meaning the material returns to its original shape when unloaded. This region of the diagram is mostly a straight line, limited by the proportional limit). This region ends at $ \sigma_Y $ (yielding). For $ \sigma \le \sigma_{pl} $, the diagram is linear, and the behavior is elastic. For $ \sigma_{pl} < \sigma < \sigma_Y $, the diagram is nonlinear, but the behavior is still elastic. Young's Modulus Hooke's law is used for small deformations in the elastic region. The Young's modulus is the slope $ E $.

Hooke's law.

$$ \sigma = E\varepsilon\ $$

Material	Young's modulus [$GPa$]
Mild Steel	210
Copper	120
Bone	18
Plastic	2
Rubber	0.02

Shear Modulus

Shear stress strain diagram

Hooke's law.

$$ \tau_{xy} = G\gamma_{xy}\ $$

Shear modulus. #v_modulus

$$ G = \frac{E}{2(1+\nu)}\ $$

In the above equation, $\nu$ refers to Poisson's ratio, further explained in a subsequent section. Only two of the three material constants (ie; $ G $, $ E $, $ \nu $) are independent in isotropic materials.

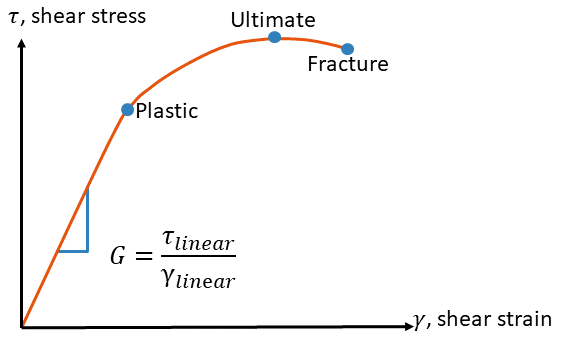
Plastic Behavior

Stresses above the plastic limit ($ \sigma_Y < \sigma $) cause the material to permanently deform.

Yield Strength

Perfect plastic or ideal plastic: well-defined $ \sigma_Y $, stress plateau up to failure. Some materials (e.g. mild steel) have two yield points (stress plateau at $ \sigma_{YL} $). Most ductile metals do not have a stress plateau; yield strength $ \sigma_{YS} $ is then defined by the 0.002 (0.2%) offset method.

Strain Hardening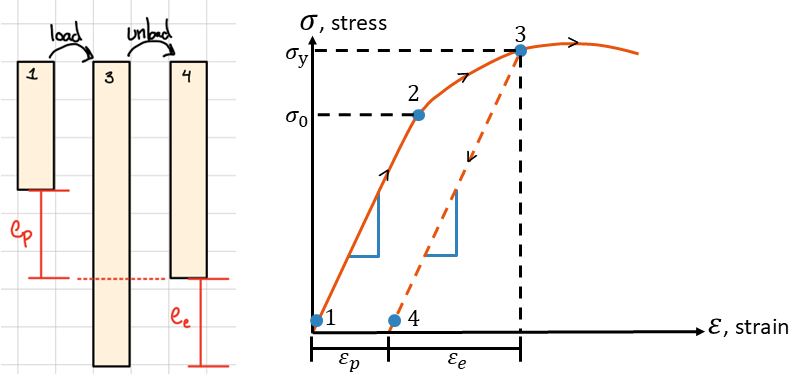

Strain hardening

Atoms rearrange in plastic region of ductile materials when a higher stress is sustained. Plastic strain remains after unloading as permanent set, resulting in permanent deformation. Reloading is linear elastic up to the new, higher yield stress (at A') and a reduced ductility.

Ultimate Strength

The ultimate strength ($ \sigma_u $) is the maximum stress the material can withstand.

Necking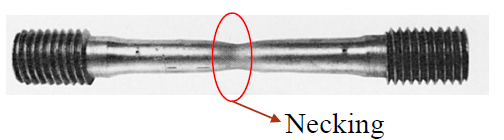

Necking

After ultimate stress ($ \sigma_u < \sigma $), the middle of the material elongates before failure.

Failure

Also called fracture or rupture stress ($ \sigma_f $) is the stress at the point of failure for the material. Brittle and Ductile materials fail differently.

Ductile materials generally fail in shear. There is a large region of plastic deformation before failure (fracture) at higher strain and necking.

Ductile failure

Axial – maximum shear stress at $45^o$ angle

Torsion – maximum shear stress at $0^o$ angle

Brittle materials are weaker in tension than shear. There is a small plastic region between yield and failure (fracture) and no necking.

Brittle failure

Axial – maximum normal stress at $0^o$ angle

Torsion – maximum normal stress at $45^o$ angle

Note the difference between engineering and true stress/strain diagrams: ultimate stress is a consequence of necking, and the true maximum is the true fracture stress.

Example: Concrete is a brittle material.

Maximum compressive strength is substantially larger than the maximum tensile strength.
For this reason, concrete is almost always reinforced with steel bars or rods whenever it is designed to support tensile loads.

Heads up!

Strain Energy builds on this content in Engineering Materals.

Deformation does work on the material: equal to internal strain energy (by energy conservation).

$$ \Delta U = \int F_{z}dz = \int \sigma_{z}(\Delta x \Delta y \Delta z)d\varepsilon_{z}\ $$

Energy density.

$$ u = \frac{\Delta U}{\Delta V} = \int \sigma_{z}d\varepsilon_{z}\ $$

Can be generalized to any deformation: areas under stress-strain curves

$$ u = \int \sigma d\varepsilon \quad \text{or} \quad u = \int \tau d\gamma\ $$

Heads up!

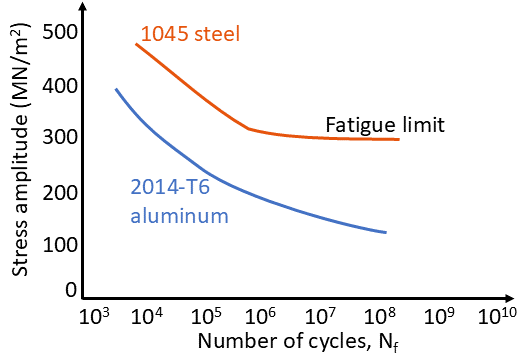
Fatigue builds on this content in Engineering Materals and Mechanical Design.

SN curve examples

If stress does not exceed the elastic limit, the specimen returns to its original configuration. However, this is not the case if the loading is repeated thousands or millions of times. In such cases, rupture will happen at stress lower than the fracture stress - this phenomenon is known as fatigue.

Other Derived Properties

Directional Materials

Isotropic: material properties are independent of the direction
Anisotropic: material properties depend on the direction (ie; composites, wood, and tissues)

Poisson's Ratio

Poisson's ratio

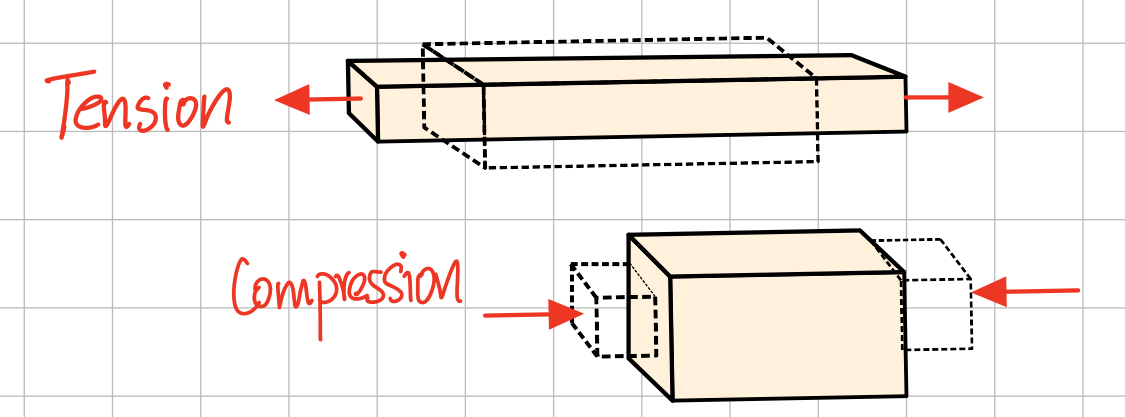
As illustrated in the figure above, when an object is being compressed it expands outward, and when stretched it will become thinner. Depending on the material, it may experience more or less lateral deformation for a given amount of axial deformation. The ratio that governs the amount of lateral strain per unit of axial strain is called Poisson's ratio.

Axial (normal) strain.

$$ \varepsilon_{x} = \frac{\delta_x}{L}\ $$

Poisson's ratio $\nu$.

$$ \nu = -\frac{\text{lateral strain}}{\text{axial strain}} = -\frac{\varepsilon_y}{\varepsilon_x} $$

Typical range. #poisson_range

$$ 0 < \nu < 0.5\ $$

Consider a cylinder with volume $ V = A\cdot L $. We know that $ A = \frac{\pi}{4}d^2 $. Since the diameter is dependant on the change in length $dx$ due to Poisson's ratio, we get

$$ \frac{\partial A}{\partial x} = 2d\frac{\partial d}{\partial x}\frac{\pi}{4} = \frac{\partial d}{\partial x}\frac{\pi d}{2} $$

We use the chain rule to find the change in volume

$$ \begin{aligned} \frac{\partial V}{\partial x} &= \frac{\partial A}{\partial x}L + \frac{\partial L}{\partial x} A \\ &= \frac{\partial d}{\partial x}\frac{\pi d}{2}L + L \frac{\pi d^2}{4} \end{aligned} $$

By definition,

$$ \nu = -\frac{\varepsilon_y}{\varepsilon_x} = -\frac{\frac{\partial d}{d}}{\frac{\partial L}{L}} = -\frac{\partial d}{d}\frac{L}{\partial L}= -\frac{\partial d}{d}\frac{L}{L\partial x} = -\frac{1}{d}\frac{\partial d}{\partial x} \implies \frac{\partial d}{\partial x} = -\nu d $$

Returning to our first equation,

$$ \begin{aligned} \frac{\partial V}{\partial x} &= \frac{\partial d}{\partial x}\frac{\pi d}{2}L + L \frac{\pi d^2}{4} \\ &= -\nu d \frac{\pi d}{2}L + L \frac{\pi d^2}{4} \\ &= -\nu \frac{\pi d^2}{2}L + L \frac{\pi d^2}{4} \\ &= \frac{\pi d^2L}{4}\left( 1- 2\nu \right) \\ &= V\left( 1- 2\nu \right) \\ \end{aligned} $$

Since $\partial V \geq 0$ and $\nu > 0$ in nicely behaved materials, $ 0 < \nu \leq 0.5$. In practice $\nu = 0.5$ only if the material is incompressible, thus in most materials $\nu < 0.5$.

Lateral strain.

$$ \varepsilon_{z} = \varepsilon_{y} = -\nu\varepsilon_{x}\ $$

Warning: Negative Poisson's Ratio (auxetics) #ngt-psn

A negative Poisson's ratio is possible when the material structure is non-trival.