Reference Pages
Mechanical Engineering

    Scroll back to top

    Axial Loading

    Pure Axial Loading Tensor

    For a scenario with only axial loading conditions, the stress tensor can be simplified as shown below.

    Axial loading stress tensor.
    $$ T= \begin{bmatrix} \frac{F_x}{A} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \ $$

    Saint-Venant's Principle: Slender Beam Case

    Notation

    Stress analysis very near to the point of application of load \( P \). Saint-Venant's principle: the stress and strain produced at points in a body sufficiently removed* from the region of external load application will be the same as the stress and strain produced by any other applied external loading that has the same statically equivalent resultant and is applied to the body within the same region.

    *farther than the widest dimension of the cross section

    Heads up!

    Stress concentration factors build on this content in engineering materials and machine failure.

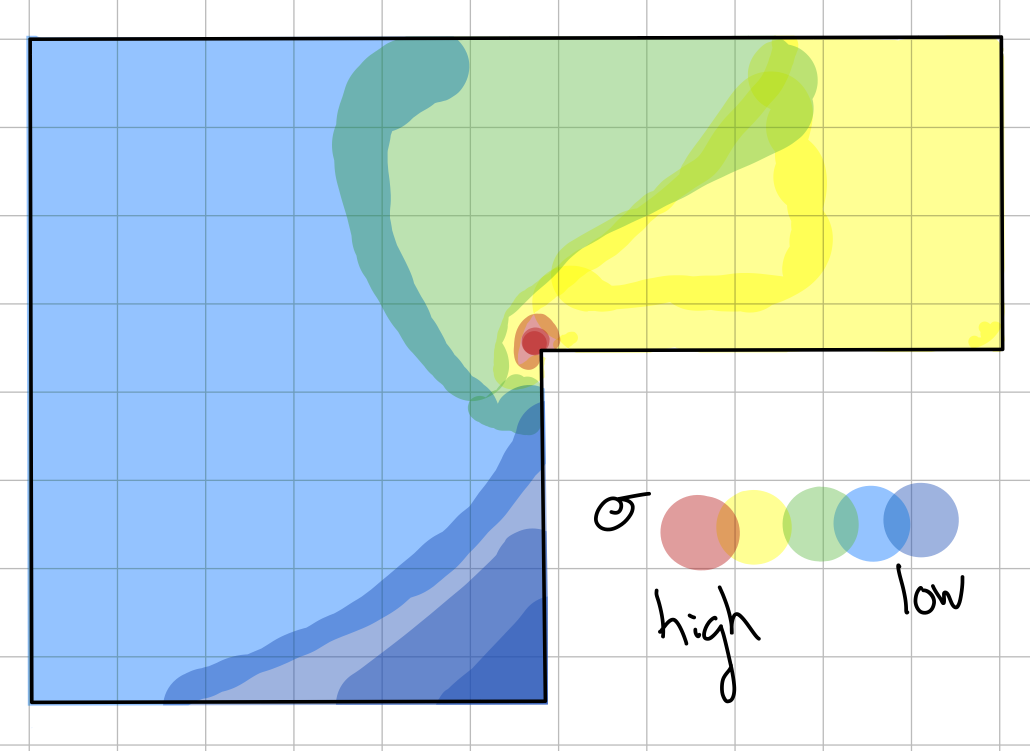
    Stress concentraions

    The stress concentration factor is the highest at lowest cross-sectional area.

    Stress concentration factor.
    $$ K = \frac{\sigma_{max}}{\sigma_{avg}}\ $$

    • Found experimentally
    • Solely based on geometry

    Force-Deformation Relation

    Relation. #axl-fdr
    $$ \delta = \frac{PL}{EA}\ $$
    $$ P = \sigma A\ $$
    $$ P = E \varepsilon A\ $$
    $$ P = E\frac{\delta}{L}A\ $$
    Axial flexibility.
    $$ \delta = fP => f = \frac{L}{EA}\ $$
    Axial stiffness.
    $$ P = k\delta => k = \frac{EA}{L}\ $$

    Axially Varying Properties

    For non-uniform load, material property and cross-section area:
    Variable properties. #sts-vpr
    $$ \delta = \int_0^L\frac{F(x)}{E(x)A(x)}dx\ $$
    $$ \sigma = E\varepsilon\ $$
    $$ \frac{F(x)}{A(x)} = E(x)\varepsilon(x)\ $$
    $$ \frac{F(x)}{A(x)} = E(x)\frac{d\delta(x)}{dx}\ $$
    $$ d\delta = \frac{F(x)}{E(x)A(x)}dx\ $$
    Assume variations with \( x \) are "mild" (on length scale longer than cross-sectional length scales)

    General Solving Procedure

    1. Draw a FBD
    2. Equilibrium equations: force balance and moment balance
    3. Constitutive equations: stress-strain or force-displacement relations
    4. Compatibility equations: geometric constraints

    Statically Determinate Problems

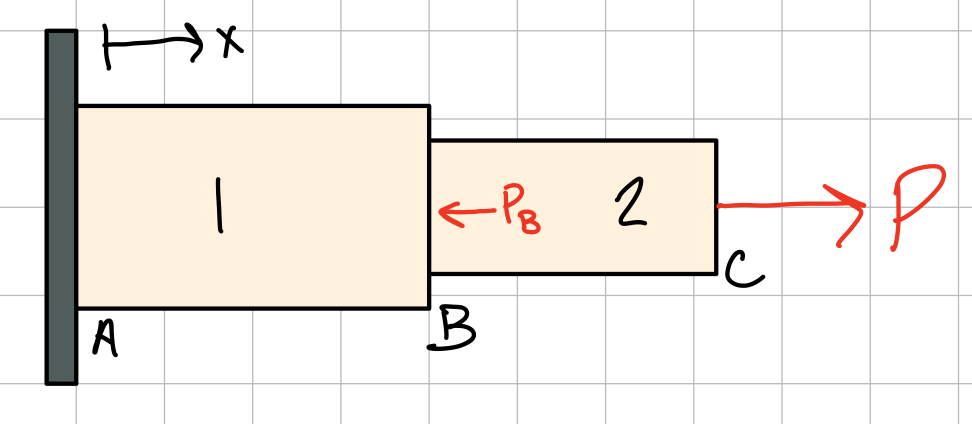
    Statically determinate
    All internal forces can be obtained from equilibrium analysis only

    Statically Indeterminate Problems

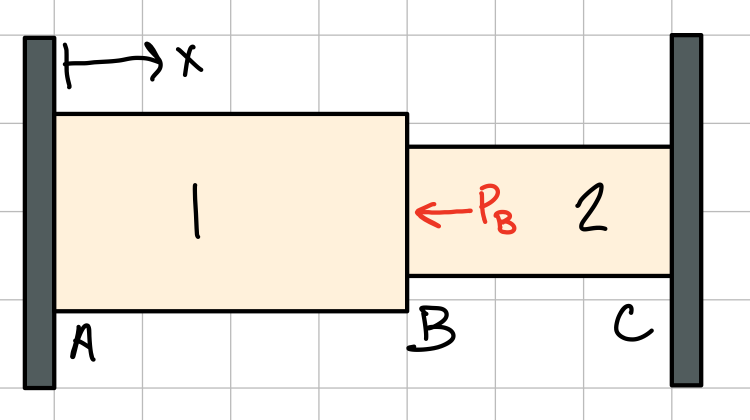
    Statically indeterminate
    Equilibrium does not determine all internal forces.

    Misfit Problems

    A misfit problem is one in which there is difference between a design distance and the manufactured length of a material. Some misfits are created intentionally to pre-strain a member. (e.g. spokes in a bicycle wheel or strings in a tennis racket). This type of problem neither modifies the equilibrium equations (1) nor the force-extension relations, (2) but the compatibility equations, (3) need to be modified.