Impact Introduction

Impact deals with loads from collisions where at least one object is moving. Intuitively, we know that impact will increase the forces that a mechanical element experiences. For example, placing a bowling ball gently on your foot would likely cause no pain, while dropping the ball from eye level would likely cause a fracture. This document will quantify the effects of impact loading in comparison to static loading, and it will discuss the design considerations engineers should make regarding impact.

Impact Theory

One easy way to quantify the effect of impact is to look at the mechanical system through the lens of energy conservation. Assuming losses are negligible, we know all of the kinetic energy of an object in motion is transferred into elastic potential energy during a collision. If we know the kinetic energy before the collision, we can determine the deformation and stress experienced as a result of the impact.

Consider the compression of an object when placing a rigid weight onto it gently. From Hooke's Law, we get

where \( W \) is the applied weight, \( k \) is the material stiffness, and \( \delta_{st} \) is the resulting deformation. If we instead dropped the weight from a height \( h \), we can find the resulting deformation by equating the initial gravitational energy with the final elastic energy.

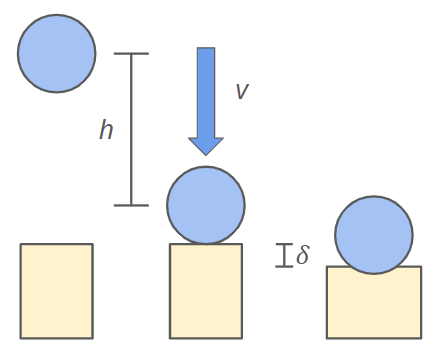
The resulting equation is

where \( \delta \) is the new deformation and the other variables are unchanged. Substituting for \( k \) using our previous expression and rearranging for \( \delta \) gives us

Deflection can also be calculated in terms of the falling object's speed. We know that just before the objects collide, all of the initial potential energy has been converted to kinetic energy. Setting up another energy balance gives us

where \( g \) is Earth's gravitational constant and \( v \) is the impact velocity. Solving for \( h \) and substituting the result into the expression for \( \delta \), we get

We define the impact factor IF as the ratio of actual deflection \( \delta \) to the static deflection \( \delta_{st} \):

Invoking Hooke's Law again, the equivalent static force causing the same deflection on the object is then

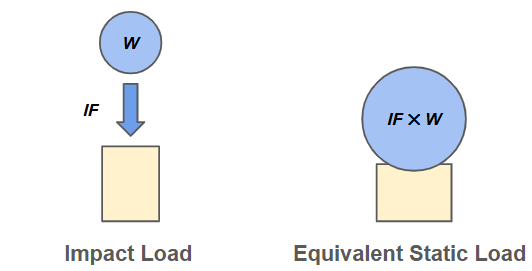
For small deflections relative to drop height (\( \delta << h \)), the deflection and equivalent force equations can be simplified:

Rewriting these equations in terms of kinetic energy \( U \), we have

Through these expressions, we see that the deflection and equivalent force both scale with the square root of kinetic energy.

Design considerations

To find the effective stress under an axial impact load, we divide equivalent force by cross sectional area. Rewriting the equation from above assuming \( \delta<<h \), the resulting equation is

Unlike static loading, the stress under impact depends on volume \( V \) rather than cross-sectional area. This means a long, thin rod will perform just as well as a short, thick rod of the same volume.

Uniform cross sections are also vital to withstanding impact loads. If one section is thicker than another, the thin section will limit the allowable force while also taking most of the impact energy. In other words, adding thickness actually makes performance worse if it sacrifices uniformity.

+

Example Problem: Example: Imact Load Beam #EX1

A compressive impact load is applied to a beam with compressive yield strength \( S_{cy} \) and dimensions described by the figure below. How much energy can it absorb?

Solution +

First, calculate the volume of the beam:

$$ V=(2L)\left(\frac{L}{2}\right)^2=\frac{L^3}{2} $$

Then, we can simply rewrite the effective axial stress equation to solve for energy absorbed and plug in the calculated volume:

$$ U=\frac{S_{cy}^2V}{2E}=\frac{S_{cy}^2L^3}{4E} $$

Instead, what if the bottom half of the beam had its width and depth doubled? How much energy can this nonuniform beam absorb?

In this case, each section of the beam must be handled separately. Calculate the volume of the top half and bottom half:

$$ V_t=(L)\left(\frac{L}{2}\right)^2=\frac{L^3}{4}; V_b=L^3 $$

The thinner top section dictates the amount of force the body can take, so the maximum stress is just the yield strength \( S_{cy} \). The energy absorbed by the top section is then

$$ U_t=\frac{S_{cy}^2V}{2E}=\frac{S_{cy}^2L^3}{8E}. $$

Simultaneously, the same force is exerted on the bottom section, but the area is four times larger, so the maximum stress is only a quarter of the stress at the top. The resulting energy absorbed is

$$ U_b=\frac{(S_{cy}/4)^2V}{2E}=\frac{S_{cy}^2L^3}{32E} $$

Sum the energy from each section for the total energy:

$$ U=U_t+U_b=\frac{S_{cy}^2L^3}{8E}+\frac{S_{cy}^2L^3}{32E}=\frac{5S_{cy}^2L^3}{32E} $$

The nonuniform beam performs worse than the uniform beam, even though it has a greater total volume! Non-uniformity can be detrimental to impact design.

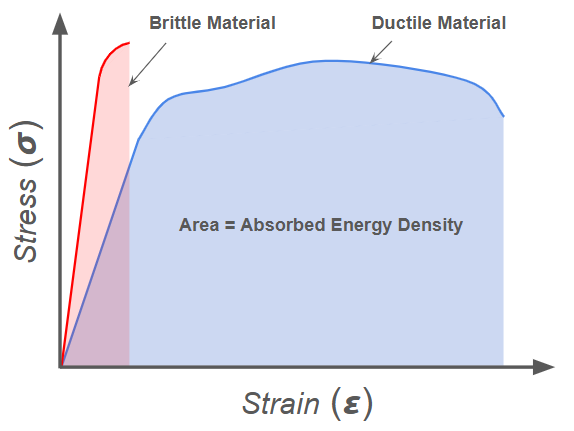
Another way to design for impact absorption is through careful material choice. Ductile materials are often better suited for impact than hard materials because even if they yield, they can handle much more strain before complete failure. This feature is evident in Stress-Strain curves, where the area under the entire curve represents the energy density before fracture.

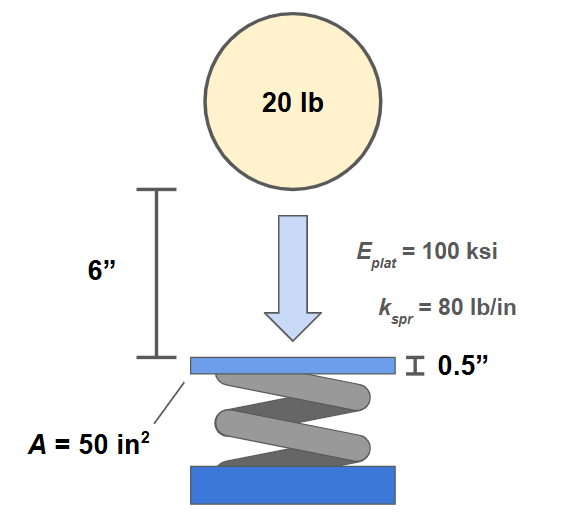
Similarly, flexible materials are uniquely helpful impact loads. In particular, using flexible supports can reduce the stresses experienced by bodies under impact, as shown in the example below.

+

Example Problem: Example: Impact Load Spring #EX2

A ball weighing 20 pounds is dropped on a platform with an elastic modulus of 100 ksi, held up by a spring with a stiffness of 20 lb/in. The drop height is 6 inches, and the platform is half an inch thick with an area of 50 square inches on the top surface. What is the effective force on the platform if the weights of the spring and platform are negligible?

Solution +

First, we calculate the static deflection of each part:

$$ \delta_{st,plat}=\frac{FL}{AE_{plat}}=\frac{(20 \text{ lb})(0.5 \text{ in})}{(50 \text{ in}^2)(100 \text{ ksi})}=2\times10^{-6} \text{ in} $$

$$ \delta_{st,spr}=\frac{F}{k_{spr}}=\frac{20 \text{ lb}}{20 \text{ lb/in}} = 1 \text{ in} $$

$$ \delta_{st}=\delta_{st,plat}+\delta_{st,spr}=1.000002 \text{ in} $$

Next, calculate the impact factor from the known static deflection:

$$ \text{IF}=1+\sqrt{1+\frac{2h}{\delta_{st}}}=1+\sqrt{1+\frac{2(6 \text{ in})}{1.000002 \text{ in}}}=4.61 $$

Now, we can easily find the equivalent static force on the platform:

$$ F_e=\text{IF} \times W=4.61(20 \text{ lb})=92.2 \text{ lb} $$

To highlight the importance of flexible supports, let's see what happens when we use a much stiffer spring (\( k=80 \) lb/in), with all else equal.

The new setup does not affect the static platform deflection, but the total deflection decreases along with the spring compression:

$$ \delta_{st,spr}=0.25 \text{ in}\xrightarrow{} \delta_{st}=0.250002 \text{ in} $$

This results in a higher impact factor and effective force:

$$ \text{IF}=8.00\xrightarrow{}F_e=160 \text{ lb} $$

The key lesson here is that using flexible supports increases the static deflection under impact. While increasing deflection is unhelpful in static loading, it reduces the impact factor and in turn reduces the stresses on the body being supported.

Unlike with static loading, ductile materials are still susceptible to stress concentrations under impact loading. Normally, ductile materials are able to redistribute stress throughout the cross section if one point yields in the presence of stress concentrations. However, in impact loading, the stress is applied so quickly that the material may not have time to deform and redistribute stress before the concentration point fails. Thus, regardless of material, stress concentrations should be factored in when designing machines with impact loading.