Reference Pages
Mechanical Engineering

    Scroll back to top

    Bending

    Transverse loads applied to a horizontal straight beam will cause it to deflect primarily up or down. This type of deformation is referred to as bending. A beam in bending will develop normal (tensile and compressive) bending stresses throughout the beam. The magnitude of these stresses depends on the internal bending moment in the beam as well as the beam's cross-section geometry.

    Sign Conventions for Shear and Moment Diagrams

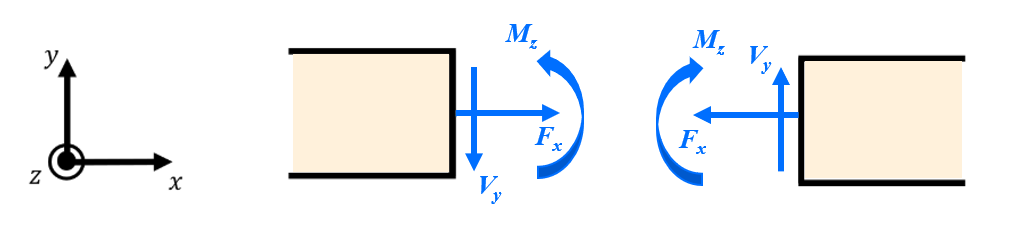
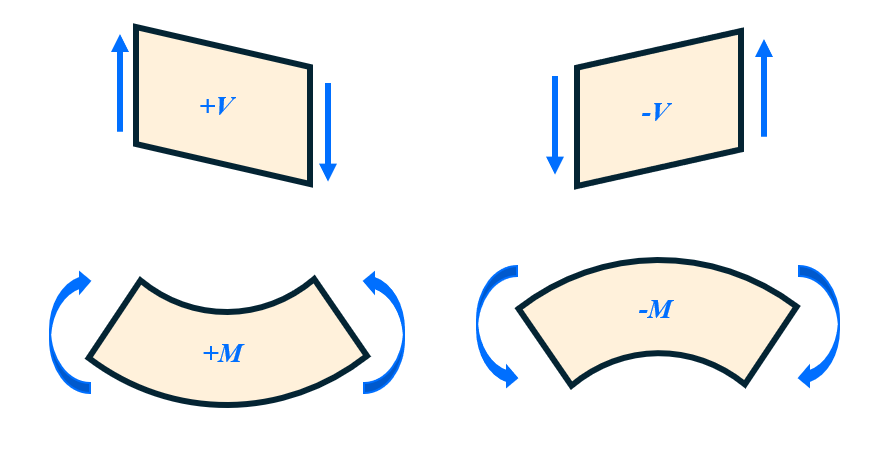
    For the purposes of drawing shear and moment diagrams, the adopted sign conventions for internal forces and moments are shown below. The internal shear force \( V \) and moment \( M \) in a beam are plotted with positive values when they act in the indicated directions with respect to internal surfaces in the beam. These conventions assume the analysis is conducted on a horizontal beam with positive \( x \) axis pointing to the right.

    Boundary Conditions

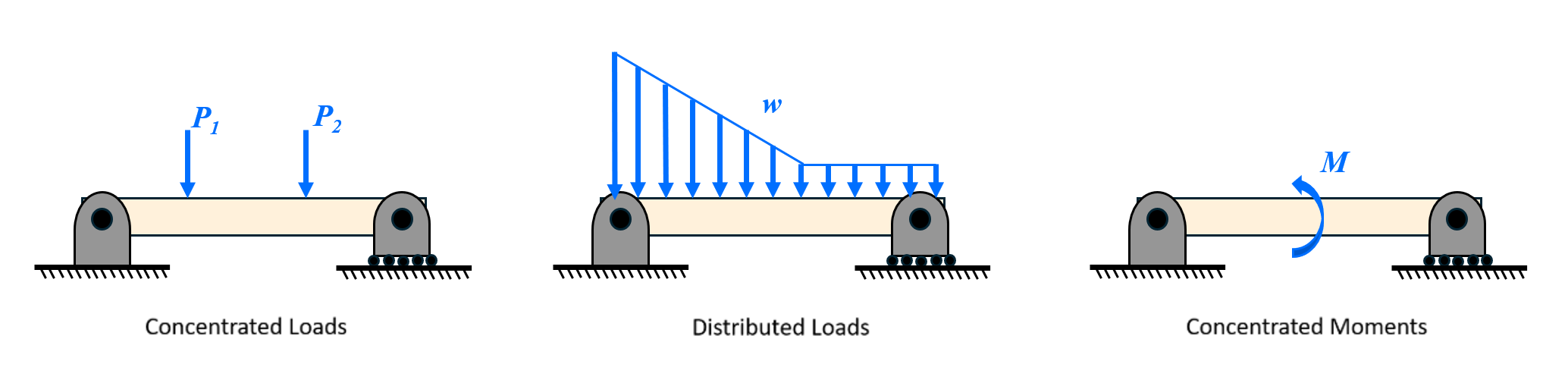
    Below are common support conditions and loading conditions that are used to model beams.

    Pin supports allow rotation but not translation; fixed supports restrain both translation and rotation of the beam at that location.

    Statically Determinate Beams
    Statically Indeterminate Beams
    Loadings

    Pure Bending

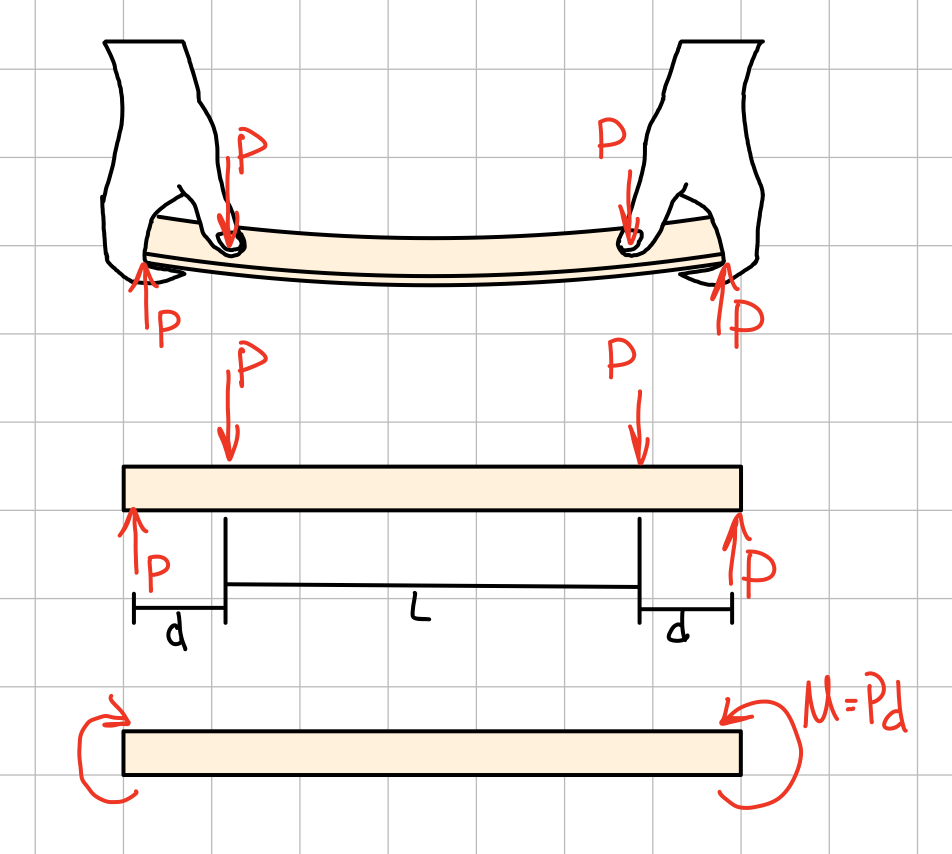
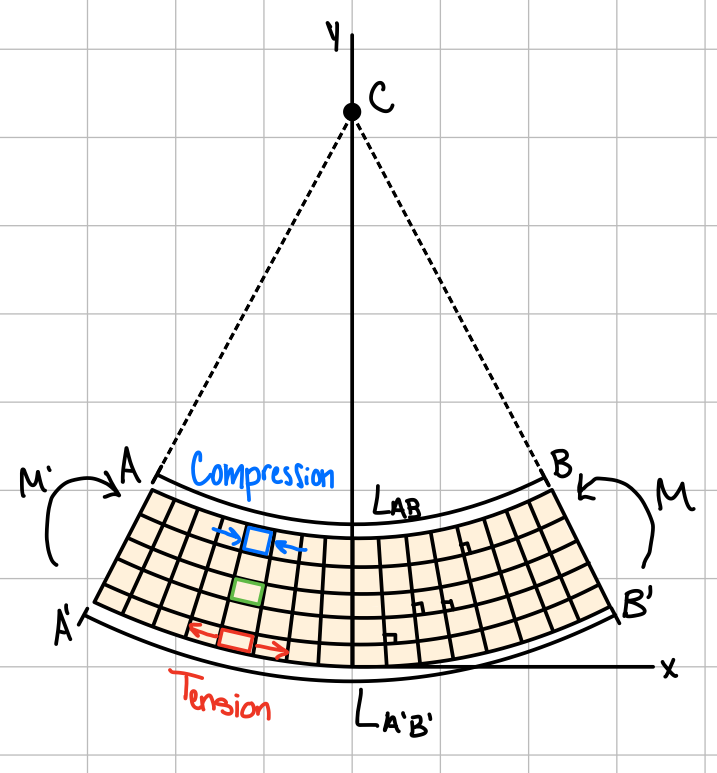
    Take a flexible strip, such as a thin ruler, and apply equal forces with your fingers as shown. Each hand applies a couple or moment (equal and opposite forces a distance apart). The couples of the two hands must be equal and opposite. Between the thumbs, the strip has deformed into a circular arc. For the loading shown here, just as the deformation is uniform, so the internal bending moment is uniform, equal to the moment applied by each hand.

    Geometry of Deformation

    Bending diagram
    Assumptions:
    • Plane sections remain plane \( \rightarrow \)no shear stress/strains.
      $$ \gamma_{xy} = \gamma_{xz} = 0\ $$
      Therefore:
      $$ \tau_{xy} = \tau_{xz} = 0\ $$
      Also, traction free boundary conditions yields...
      $$ \sigma_y = \sigma_z = \tau_{yz} = 0\ $$
    • There is a Neutral axis between the top and the bottom where the length does not change.
      $$ \sigma_x = 0 \rm\ and \rm\ \epsilon_x = 0\ $$
    • The beam deforms into a circular arc where the top surface (\( AB \)) is in compression
      $$ \sigma_x, \varepsilon_x <0 $$
      , and the bottom surface (\( AB ^\prime \)) is in tension
      $$ \sigma_x, \varepsilon_x >0 $$
      .
    • Any point in the beam is in a state of uniaxial normal stress.
    • Finding stresses is a statically indeterminate problem.

    Stress-Strain Variations

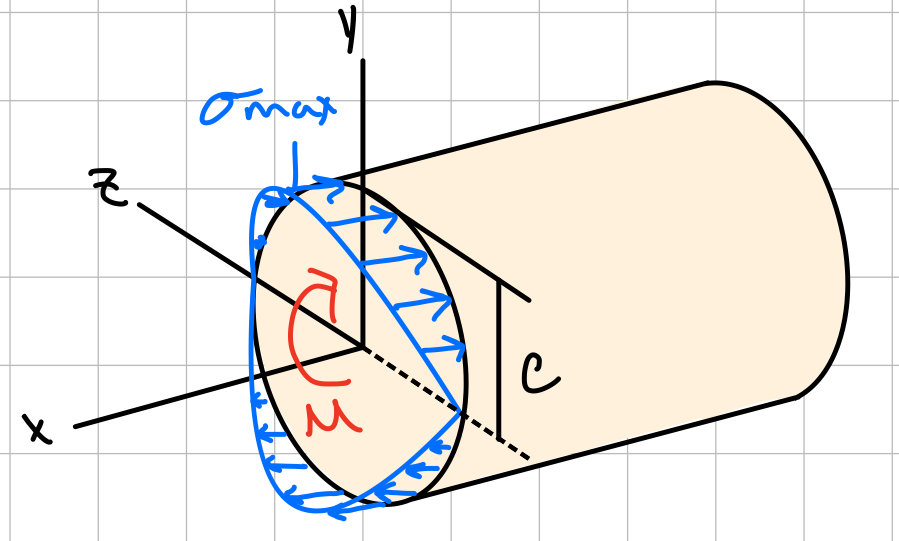
    The magnitudes of stress and strain vary along the cross section. The magnitudes increase as the point of intrest moves away from the neutral axis. The maximum is at the point farthest away from the neutral axis.
    This variation also changes as more moads are added.

    Material Behavior: linear elastic beams

    Elastic range: bending moment is such that the normal stresses remain below the yield strength.
    Hooke’s law combined with equilibrium.
    $$ \int_A y dA =0\ $$
    Moment-curvature equation. #mmt-crv
    $$ M(x) = \frac{E(x)I_z(x)}{\rho(x)}\ $$
    Constitutive Relationship:
    $$ L_{y_i} = L_{NAi} = L_{NAf} = \rho\theta\ $$
    $$ L_{y_f} = (\rho - y)\theta\ $$
    $$ \varepsilon_x = \frac{(\rho-y)\theta - \rho\theta}{\rho\theta}\ $$
    $$ \varepsilon_x = \frac{-y\theta}{\rho\theta} = \frac{-y}{\rho}\ $$
    $$ \sigma_x = E\varepsilon_x = -\frac{Ey}{\rho}\ $$
    Force Equilibrium:
    $$ \Sigma F_x = 0\ $$
    $$ \Sigma F_x = \int dF\ $$
    $$ \Sigma F_x = \int \sigma_x dA\ $$
    $$ \Sigma F_x = \int\frac{-Ey}{\rho}dA\ $$
    $$ \Sigma F_x = \frac{-E}{\rho}\int y dA = 0\ $$
    Moment Equilibrium:
    $$ \Sigma M_z = -M - \int y dF = 0\ $$
    $$ \Sigma M_z = -M - \int y\sigma_x dA\ $$
    $$ \Sigma M_z = -M - \int y (\frac{-Ey}{\rho}) dA\ $$
    $$ \Sigma M_z = -M - + \frac{E}{\rho} \int y^2 dA = 0\ $$

    First Moment of Area: Centroid of an Area

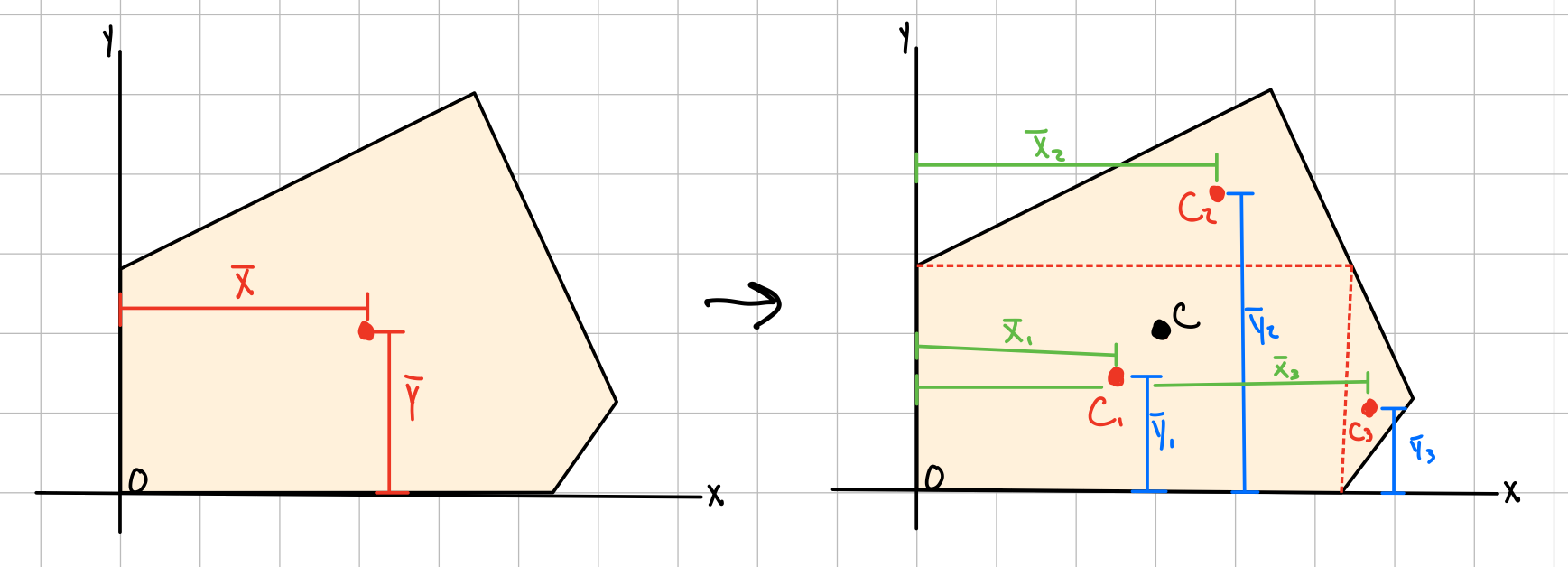
    The first moment of the area A with respect to the z-axis is given by \( Q_x = \int_A y dA = \Sigma yA \) . The first moment of the area A with respect to the y-axis is given by \( Q_y = \int_A x dA = \Sigma zA \). \( (\overline{x}, \overline{y}) \)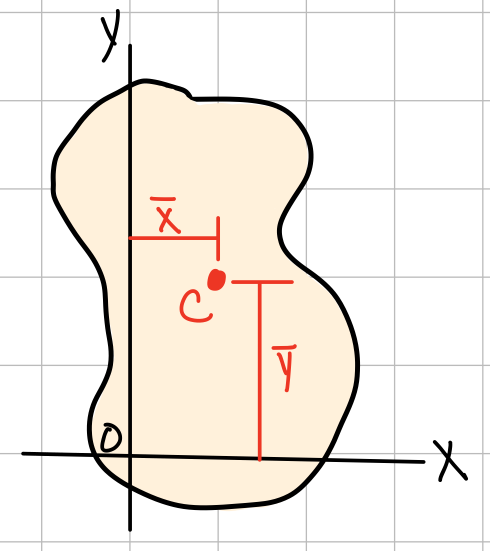
    Centroid of a body
    x coordinate.
    $$ \bar{x} = \frac{1}{A}\int_A x dA\ $$
    y coordinate.
    $$ \bar{y} = \frac{1}{A}\int_A y dA\ $$
    Complex (or composite) areas can be divided into smaller, easier parts.
    Centroid of a composite body
    Composite x coordinate
    $$ \bar{X} = \frac{1}{A_{tot}}\sum_i (A_i\bar{y}_i)\ $$
    Composite y coordinate
    $$ \bar{Y} = \frac{1}{A_{tot}} \sum_i (A_i\bar{y}_i) $$

    Second Moment or Area Moment of Inertia

    The moment of inertia of the area \( A \) with respect to the x-axis.
    x-axis second moment.
    $$ I_x = \int_A y^2 dA $$
    The moment of inertia of the area \( A \) with respect to the y-axis.
    y-axis second moment.
    $$ I_y = \int_A x^2 dA $$

    Note: polar moment of inertia in this plane
    Polar moment of Inertia.
    $$ J = \int_A \rho^2 dA = \int_A (y^2 + x^2)dA = I_y + I_x\ $$
    Parallel-axis theorem: the moment of inertia about an axis through C parallel to the axis through the centroid C is related to \( I_C \).
    Parallel axis theorem.
    $$ I_C = I_{C'} +A'd_{CC'}^2\ $$

    Summary: Moment of Inertia

    Common shapes about the origin: \( I \) and \( J_O \)
    Common shapes about the centroid: \( \bar{I} \) and \( J_c \)
    ShapeDiagramEquations
    Rectangle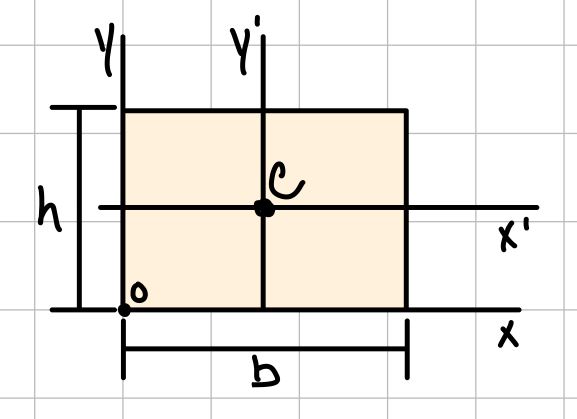
    		\( \bar{I_{x'}} = \frac{1}{12}b h^3 \)

    \( \bar{I_{y'}} = \frac{1}{12}b^3 h \)

    \( I_x = \frac{1}{3}b h^3 \)

    \( I_y = \frac{1}{3}b^3 h \)

    \( J_c = \frac{1}{12}bh(b^2+h^2) \)
    Triangle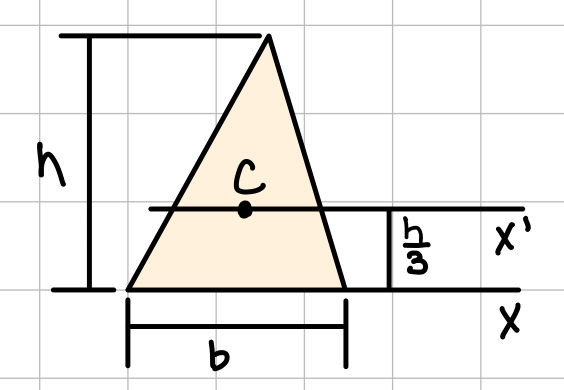
    		\( \bar{I_{x'}} = \frac{1}{36}bh^3 \)

    \( I_x = \frac{1}{12}bh^3 \)
    Circle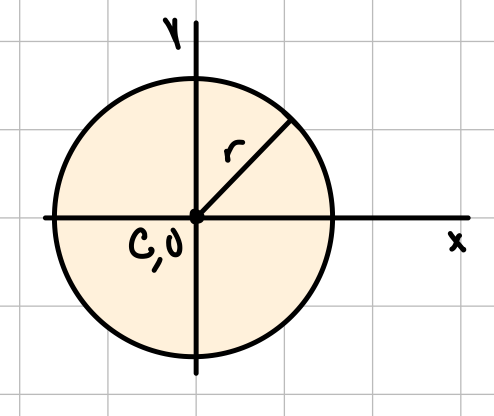
    		\( \bar{I_x} = \bar{I_y} = \frac{1}{4} \pi r^4 \)

    \( J_O= \frac{1}{2} \pi r^4 \)
    Semicircle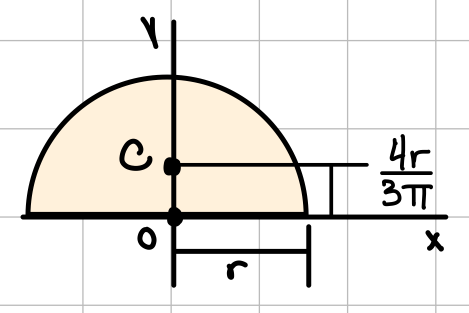
    		\( I_x = I_y = \frac{1}{8} \pi r^4 \)

    \( J_O = \frac{1}{4} \pi r^4 \)
    Quarter circle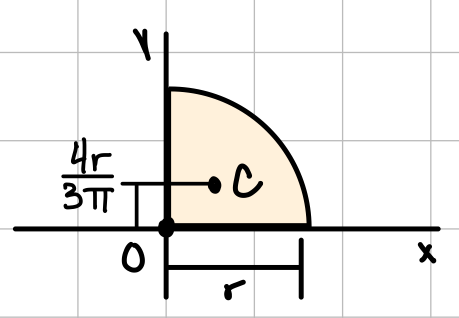
    		\( I_x = I_y = \frac{1}{16} \pi r^4 \)

    \( J_O = \frac{1}{8} \pi r^4 \)
    Ellipse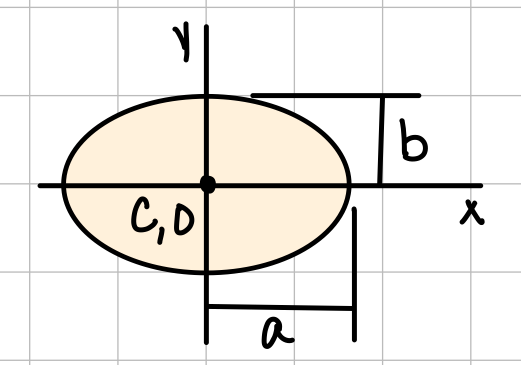
    		\( \bar{I_x} = \frac{1}{4} \pi a b^3 \)

    \( \bar{I_y} = \frac{1}{4} \pi a^3 b \)

    \( J_O = \frac{1}{4} \pi ab(a^2+b^2) \)
    Mass moment of inertiaArea moment of inertia
    Other namesFirst moment of areaSecond moment of areaPolar moment of area
    Description Determines the torque needed to produce a desired angular rotation about an axis of rotation (resistance to rotation) Determines the centroid of an area Determines the moment needed to produce a desired curvature about an axis(resistance to bending) Determines the torque needed to produce a desired twist a shaft or beam(resistance to torsion)
    Equations
    $$ I_{P,\hat{a}} = \iiint_\mathcal{B} \rho r^2 \,dV\ $$
    $$ Q_z = \int_A y dA = \Sigma yA $$
    $$ Q_y = \int_A z dA = \Sigma zA $$
    $$ \bar{y} = \frac{1}{A}\int_A y dA $$
    $$ \bar{z} = \frac{1}{A}\int_A z dA $$
    $$ I_x = \int_{A}^{} y^2 \,dA \ $$
    $$ I_y = \int_{A}^{} x^2 \,dA \ $$
    $$ \begin{aligned} J_O &= \int_{A}^{} r^2 \,dA \\ &= \int_{A}^{} (x^2+y^2) \,dA\ \end{aligned} $$
    Units\( mass*length^2 \)\( length^3 \)\( length^4 \)\( length^4 \)
    Typical Equations
    $$ \tau = I\alpha $$
    $$ \tau = \frac{VQ}{It} $$
    $$ \sigma = (My)/I $$
    $$ \tau = \frac{VQ}{It} $$
    $$ \tau = \frac{T\rho}{J} $$
    Courses TAM 212 TAM 251 TAM 210, TAM 251 TAM 251

    Maximum Normal Stress

    From equilibrium: the centroid is located at \( \bar{y}=0 \), i.e., the neutral axis passes through the centroid of the section.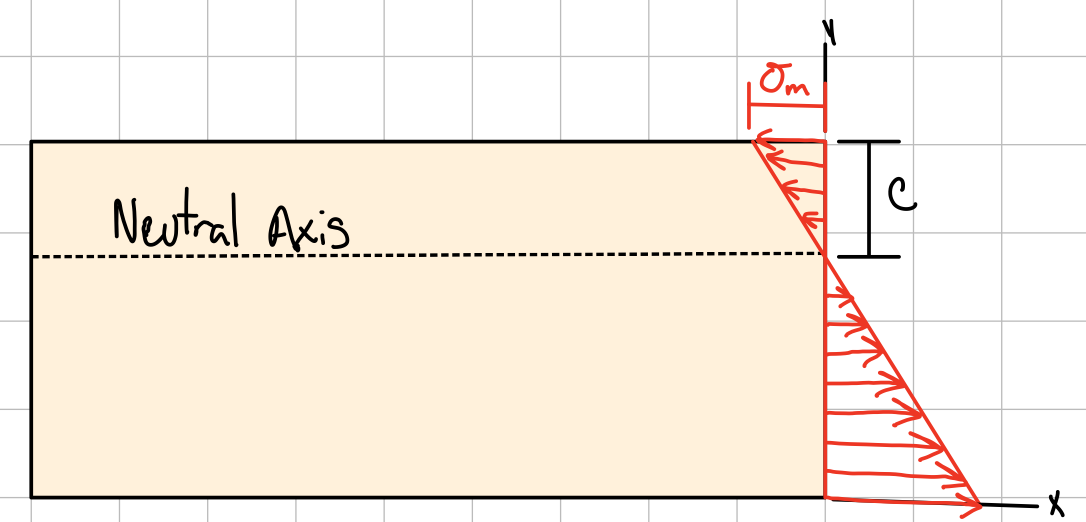
    Elastic flextural formula. #ela-flx
    $$ \sigma_x (x,y) = - \frac{M(x)y}{I_z(x)}\ $$
    $$ M_z = \frac{EI_z}{\rho}\ $$
    $$ M_z = \frac{-\sigma_x}{y}I_z\ $$
    To evaluate the maximum absolute normal stress, denoting “c” the largest distance from the neutral surface, we use:
    Absolute maximum stress.
    $$ \sigma_{max} = \frac{|M|c}{I_z}\ $$
    Note: the ratio I/c depends only upon the geometry of the cross section. This ratio is called the elastic section modulus and is denoted by S.
    Absolute maximum stress.
    $$ \sigma_{max} = \frac{|M|}{S}\ $$
    Elastic section modulus.
    $$ S = \frac{I}{c}\ $$

    Heads up! - Extra

    Composite beams builds on this content.

    Recall that \( \epsilon_x = -\frac{y}{\rho} \) does not depend on the material properties of the beam, and is based only on the assumptions of geometry done so far.

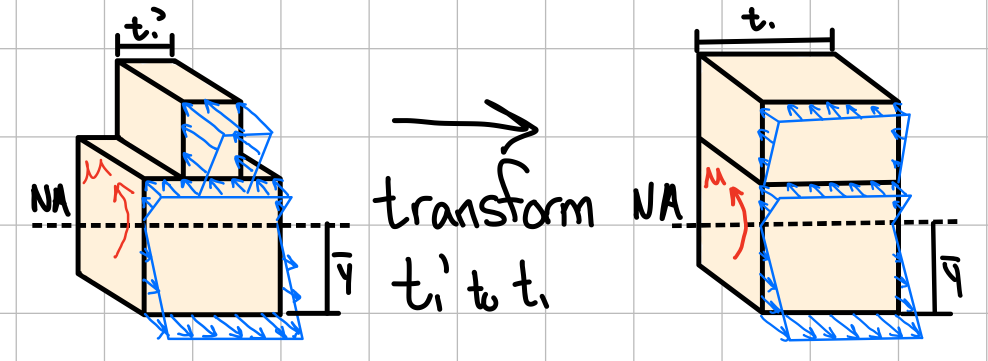
    In non-homogeneous beams, we can no longer assume that the neutral axis passes through the centroid of the composite section. We should now determine that location…
    After obtaining the TRANSFORMED CROSS SECTION, we get
    $$ \int_{A_t}y d A_t = 0\ $$
    Therefore, the neutral axis passes through the centroid of the transformed cross section.
    Note: the widening (\( n > 1 \)) or narrowing (\( n < 1 \)) must be done in a direction parallel to the neutral axis of the section, since we want y-distances to be the same in the original and transformed section, so that the distance y in the flexural formula is unaltered.
    $$ \sigma_1 = -\frac{My}{I_t}\ $$
    $$ \sigma_2 = -\frac{nMy}{I_t}\ $$

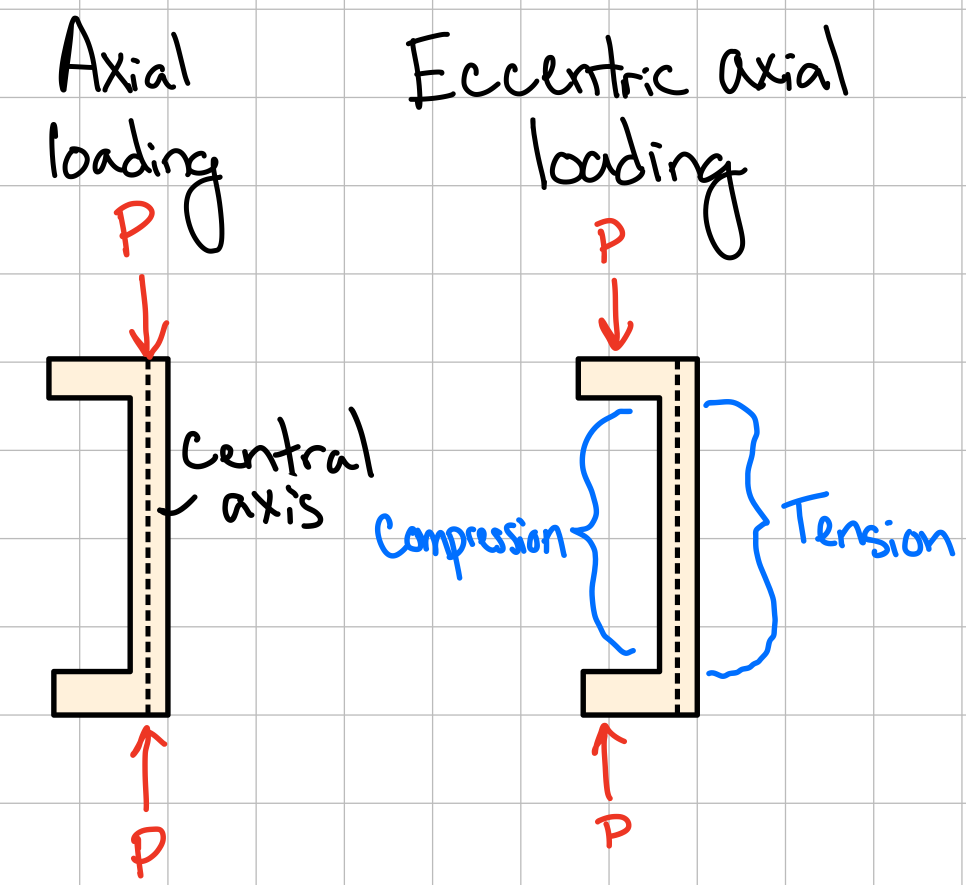
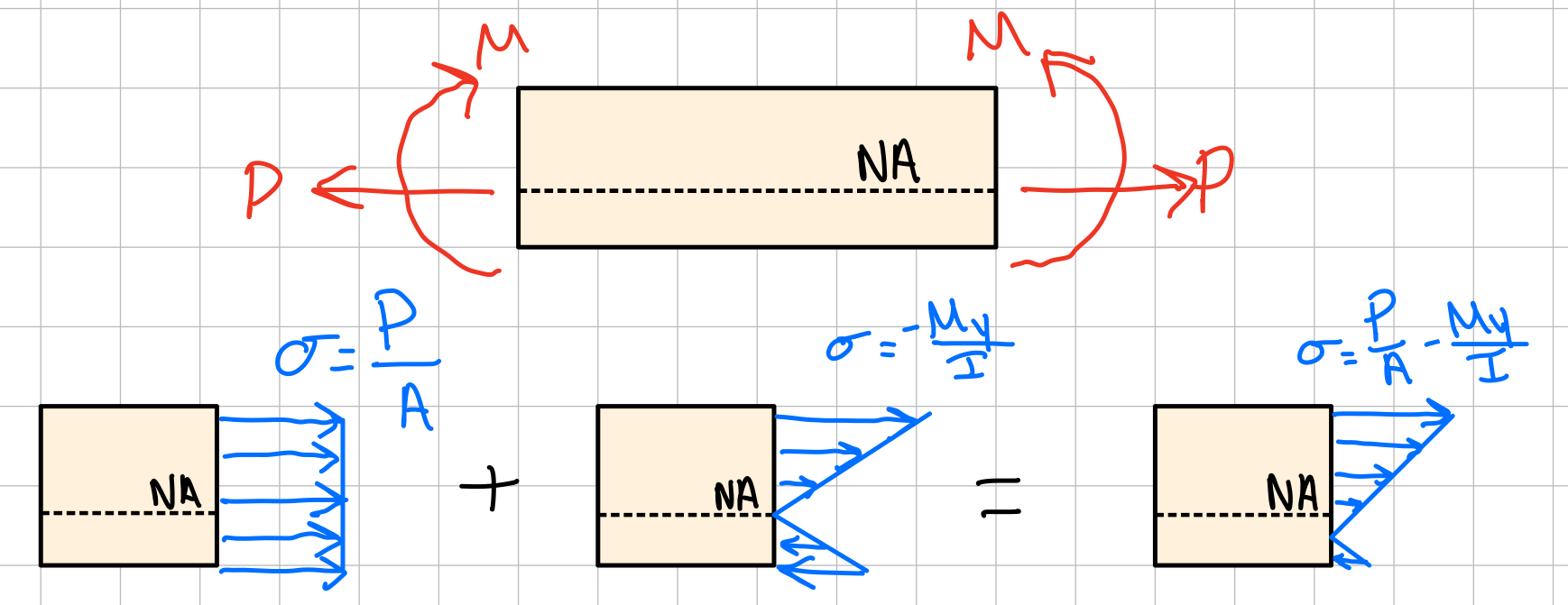
    Eccentric Axial Loading in a Plane of Symmetry

    Equilibrium.
    $$ F=P \ \ \text{and} \ \ M=Pd\ $$
    Stress due to eccentric loading found by superposing the uniform stress due to a centric load and linear stress distribution due to a pure bending moment. Validity requires stresses below proportional limit (elastic region), deformations have negligible effect on geometry, and stresses not evaluated near points of load application.