\( \delta_T \) , \( \varepsilon_T \) present in addition to elastic \( \delta_E \) , \( \varepsilon_E \) (from internal forces). Superposition (small strains):
Total strain.
$$ \varepsilon_{tot} = \varepsilon_{E} + \varepsilon_{T}\ $$
Total displacement.
$$ \delta_{tot} = \delta_{E} + \delta_{T}\ $$
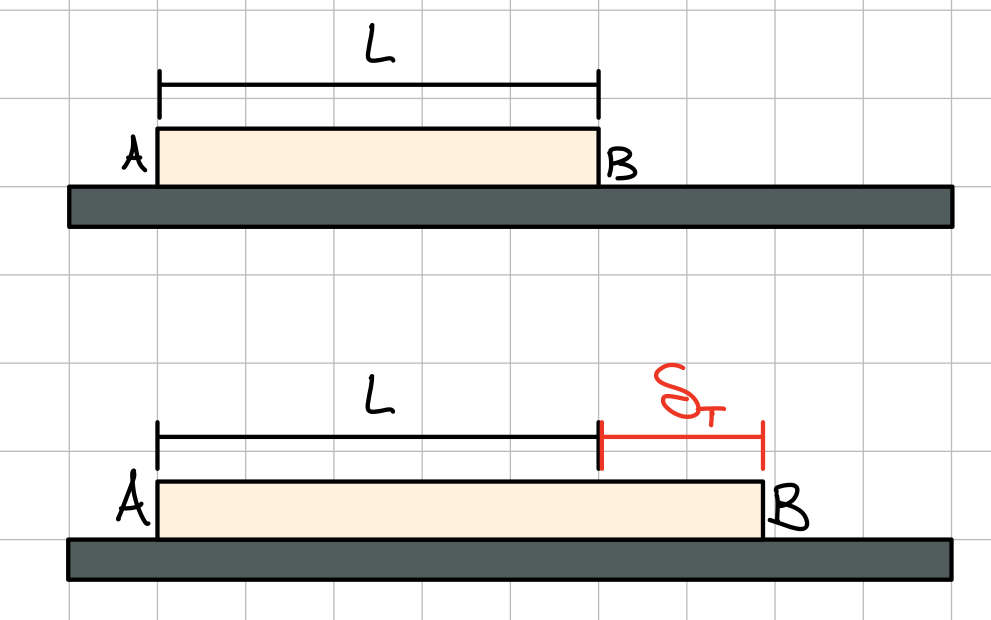
Temperature changes with no applied loads
A rod rests freely on a smooth horizontal surface. Temperature of the rod is raised by \( \Delta T \). Rod elongates by an amount.
Displacement from temperature changes.
$$ \delta_{T} = \alpha \Delta T L\ $$
Linear coefficient of thermal expansion \( \alpha \), \( [\alpha] = \frac{1}{K},\frac{1}{°C},... \). This deformation is associated with an average thermal strain:
Strain from temperature changes.
$$ \varepsilon_{T} = \frac{\delta_T}{L} = \alpha T\ $$
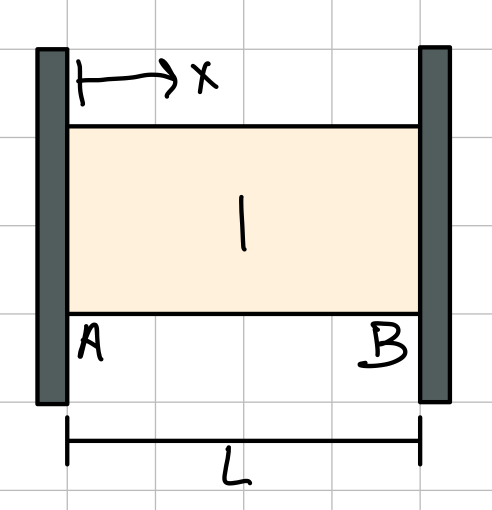
Temperature changes with statically indeterminate beam
Initially, rod of length \( L \) is placed between two supports at a distance \( L \) from each other. With no internal forces, there is no stress or strain.
Force balance.
$$ R_{A} = R_{B} = 0\ $$
Reaction force.
$$ R_{A} = F\ $$
After raising the temperature, total elongation of the rod is still zero. The total elongation is given by:
Total elongation.
$$ \delta = \frac{FL}{EA} + \alpha L \Delta T = 0\ $$
The stress in the rod due to change in temperature is given by:
Stress from temperature changes.
$$ \sigma = -\alpha E \Delta T\ $$