Current page:

Friction

Friction is a force that resists the movement of two contacting surfaces sliding relative to each other. Frictional forces act tangential to the surface at the point of contact and act in opposition to the possible or existing motion between the surfaces. In TAM 210/211, we will focus on dry friction. Dry friction occurs between two surfaces with no lubricating fluid between them.

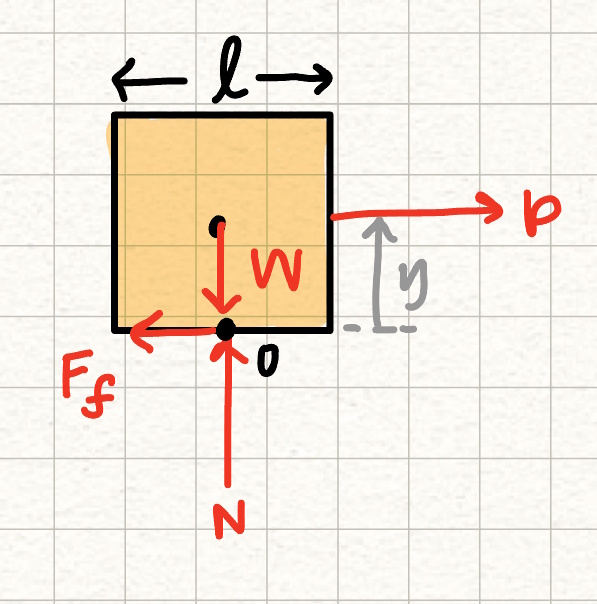
Consider a box with applied load $ P $ and weight $ W $ sitting on a rough surface. The box has normal force $ N $ and frictional force $ F_f $ opposing the motion of the box:

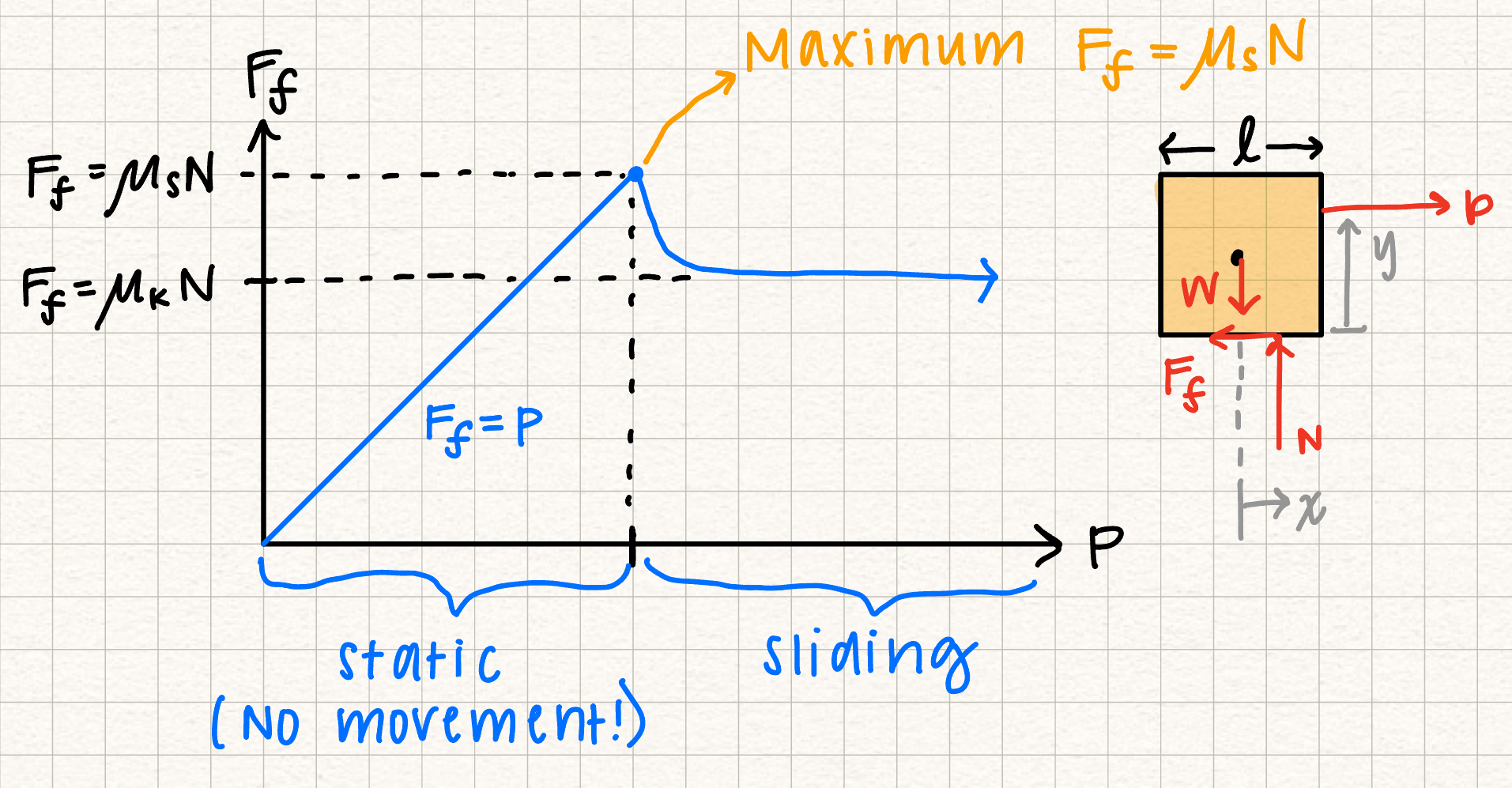
With a very small applied load, the box won't move. However, at some point, with a large enough $ P $, the box will start to slide along the surface.

Writing the equations of equilibrium of the box and solving for $ P $ results in $ P = F_f $. As the applied load increases, the frictional force will also increase. This is indicated by the straight line on the $ F_f $ vs. $ P $ graph. Once the frictional force reaches a maximum, the box will begin to slide on the surface.

The maximum static frictional force is written as:

Limit on static friction force magnitude.

$$ F_f \le \mu_s N $$

Variables $ F_f $ and $ N $ are the magnitude of the friction force $ \vec{F_f} $ and the normal force $ \vec{N} $, and $ \mu_s $ is the coefficient of static friction.

Did you know?

Mabuchi et al. conducted a study in 2012 to examine the coefficient of static friction of a banana peel!

They found banana peels to be almost 6x as slippery as the floor, with $ \mu_s $= 0.066! They also examined other fruit peels and found apples have a $ \mu_s $ of 0.125, orange peels have a $ \mu_s $ of 0.198, and tangerine peels are the least slippery with $ \mu_s $ = 0.225.

Image from Mabuchi, Kiyoshi, et al. "Ig Nobel Prize-winning episode: Trip from a slip on a banana peel to the mysterious world of mucus." Biosurface and Biotribology 2.3 (2016): 81-85.

This study won the 2014 Ig Nobel Prize, which recognizes unusual scientific achievements. Insights gained from the study could help with undertanding more about how articular joints are lubricated and move.

Static Friction

Static friction is the friction between two bodies when there is no movement between them. Examples of coefficients of static friction:

System	Static friction $\mu_s$
Rubber on dry concrete	1.0
Wood on wood	0.5
Steel on steel	0.6
Shoes on wood	0.9
Shoes on ice	0.1

Did you know?

Articular cartilage lines the end of your bones at joints, where two bones come together in your body. It acts as a smooth surface that allows your bones to slide past each other when your body is moving.

Articular cartilage is very slippery and has a very small coefficient of friction: as low as 0.001! This is similar to the coefficient of friction between two pieces of ice!

Tipping vs. Slipping

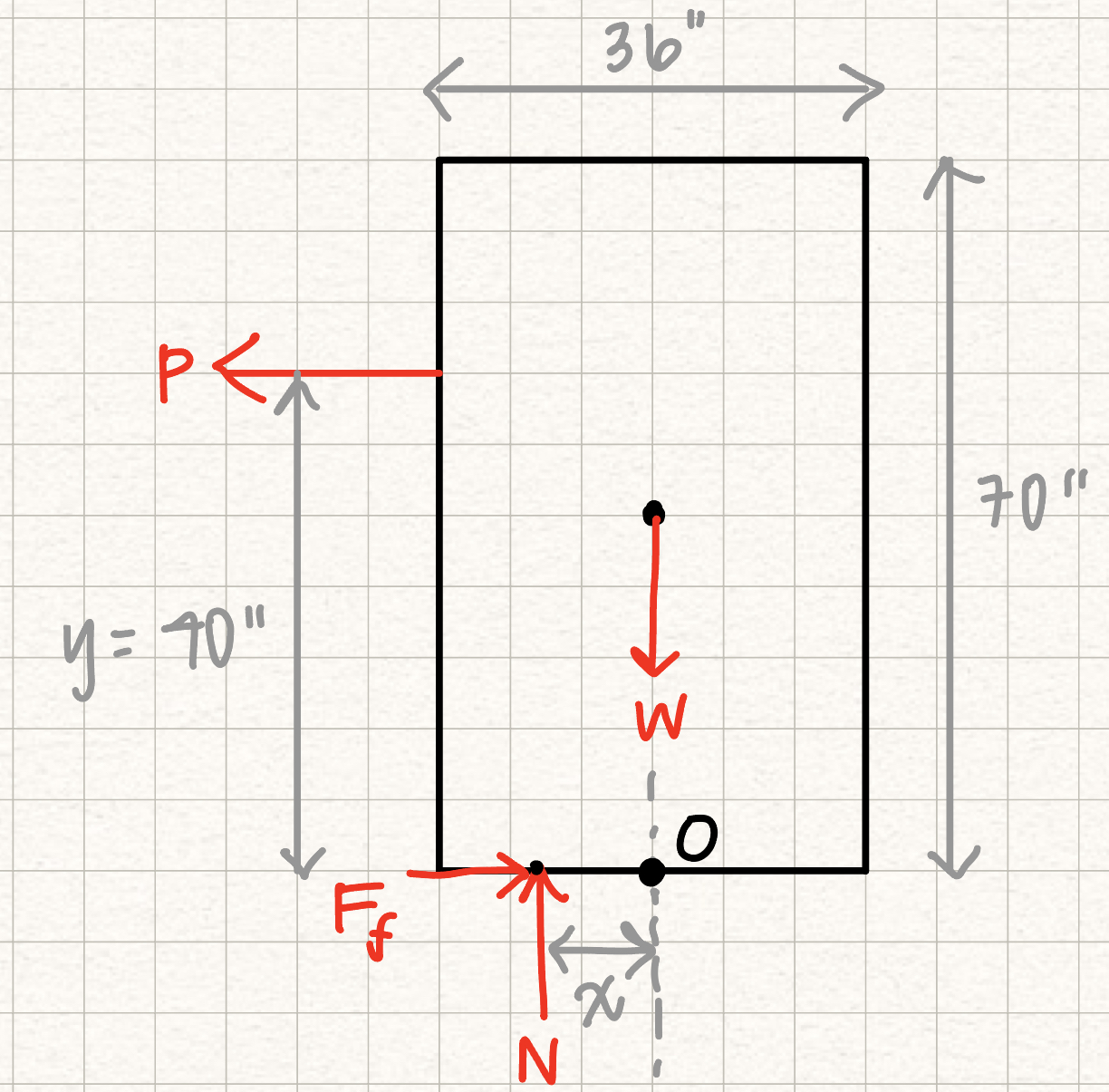
Consider a box of length l that is sitting on a rough surface with an applied load P on the right side. As P increases, there are two possible scenarios: either the box will "slip" and start sliding along the surface, or the box will tip onto the right corner.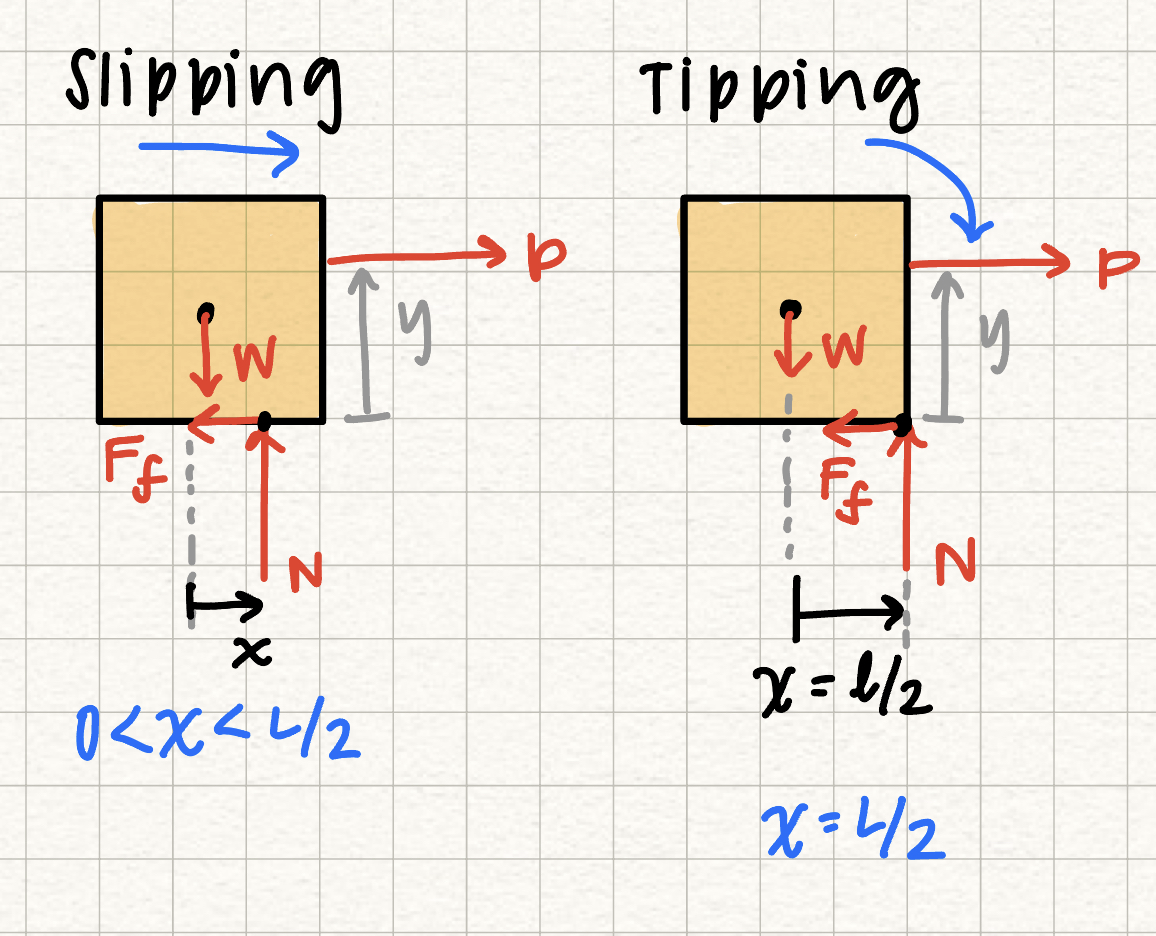

tipping vs. slipping

If the box experiences slipping, the normal force will act at a location x from the center of the box. The frictional force can be written as

$$ F_f = \mu_s N $$

You can use the other equations of equilibrium to solve for the force P required for the box to slip.

If the box experiences tipping, the normal force will act at the bottom right corner of the box, and the couple from the frictional force and N will create a moment causing the box to tip.

To determine which of these scenarios will occur, you should write the equations of equilibrium for each case and solve for the force P required to cause either slipping or tipping. Whichever condition has the smallest force P will be the condition that occurs.

Note: See the derivation below for an explanation of why the normal force does not act at the center of mass of the box.

Location of Normal Force: Derivation #nfl

$$ $$

If the normal force N acted at the middle of the box (at the center of mass), we would write the three equations of equilibrium as follows:

$$ \sum F_x = P - F_f = 0 $$

$$ \sum F_y = N - W = 0 $$

So far, so good! However, we run into a problem when we write the sum of moments equation:

$$ \sum M_O = -Py = 0 $$

The sum of moments equation about point O results in an expression that is not possible: we know that P cannot be zero, so there must be some sort of moment about the center of the box from the normal force acting offset from the center of mass of the box.

Example Problem: Frictional forces on a fridge: Slipping and Tipping #undefined

Given: Fridge weight = 250 lb and $ \mu_s $ = 0.4

Find: The maximum horizontal force P that can be applied without causing movement of the fridge

Drawing a FBD of the fridge yields:

We will then use the FBD and equations of equilibrium to solve for the force $ P $ necessary to make the fridge tip, and make the fridge slip along the surface:

Assume slipping, max $ F = \mu_s \ N $

$$ \begin{aligned} \sum{F_x} &= 0 \\ P - F &= 0 \\ P &= F \\ \sum{F_y} &= 0 \\ N - W &= 0 \\ N &= W \end{aligned} $$

If $ P = F \leq \mu_s \ N $ , the fridge won't slide
Max $ P $ before sliding:

$$ P = F = \mu_s \ N = \mu_s \ W = 0.4 \ (250 \ lb) = 100 \ lb $$
Check to see if it is tipping at $ P = 100 \ lb $, solve for $ x $

$$ \begin{aligned} \sum{M_o} &= P_y - N_x = 0 \\ x &= \frac{P_y}{N} = \frac{P_y}{W} = \frac{100 \ lb \ (40 \ in)}{250 \ lb} = 16'' \end{aligned} $$

If $ x = 18 '' $ , the fridge would tip. Because $ x = 16 '' $ , the fridge is not tipping!
Assume tipping, solve for $ P $

$$ \begin{aligned} \sum{F_x} &= 0 \\ P - F &= 0 \\ P &= F \\ \sum{F_y} &= 0 \\ N - W &= 0 \\ N &= W \\ \sum{M_o} &= 0 \\ P_y - N_x &= 0 \\ P &= \frac{N_x}{y} = \frac{W_x}{y} = \frac{250 \ lb \ (18 \ in)}{40 \ in} \\ P &= 112.5 \ lb \quad \text{for tipping} \end{aligned} $$

Min $ P $ for sliding: 100 lb
Min $ P $ for tipping: 112.5 lb
Fridge will slide at $ P=100 \ lb $