Reaction forces
Because of Newton's Third Law we know that every action has an equal and opposite reaction. We can solve for these reaction forces to understand the loading of a structure.Types of connections
Different supports and different connections have different types of reaction forces depending on what they are constraining. For example, a pin connection restricts movement in the x-and y-directions but doesn't restrict rotation. This means that each pin connection has two reaction forces: one in the x-direction, and one in the y-direction corresponding to the degrees of freedom that are fixed. A roller support only constrains movement in the y-direction, and thus only has one reaction force (oriented in the y-direction).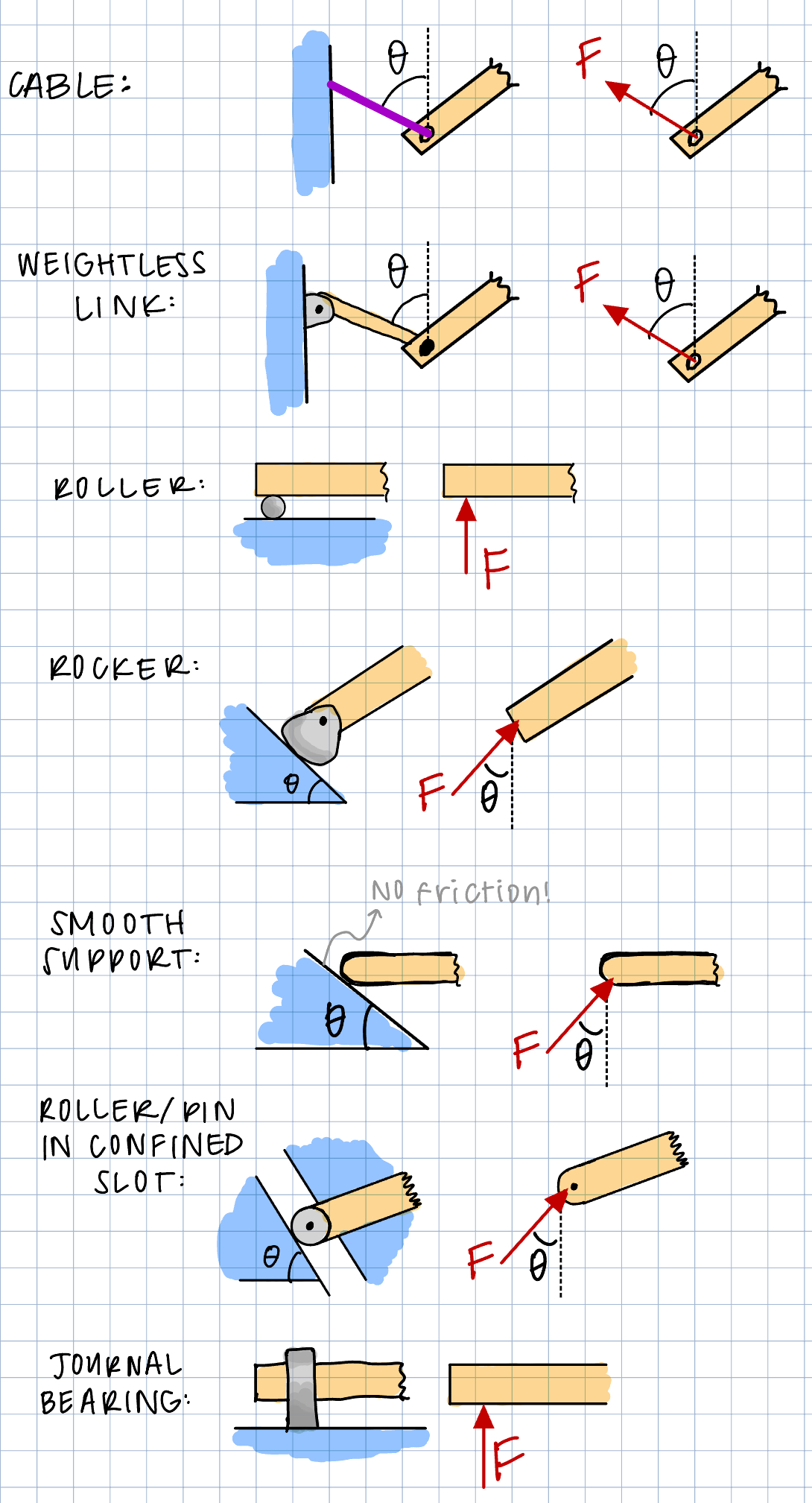
Application alert!
Track and field starting blocks use Types of connections by returning a force normal to the surface back into the runner.

The resultant reaction force created by the applied forces can be calculated through basic vector addition.
Application alert!
The Krannert Center parking garage uses Types of connections by using elastomeric bearing pads.

Elastomeric bearing pads are incorporated below columns supporting the roof of the Krannert Center parking garage. Elastomeric bearing pads behave similarly to roller supports in that they allow for horizontal movement, but provide an upwards reaction force in the vertical direction. Learn more about elastomeric bearing pads here. You can learn more about the Krannert Center for the Performing Arts here.
Heads up!
Slider cranks builds on this content in dynamics.
The slider component of a slider crank mechanism has a reaction force like the "Roller/pin in confined slot" connection shown to the left.
Redundant constraints
If a body has more supports than it needs to hold it in equilibrium, it is overly constrained. This will result in more unknown reaction forces than equations we can write, and the problem will not be solvable using statics alone. This type of system is a "statically indeterminate" system. In a 2D system, we can write three equilibrium equations (forces in the x and y directions and moments about a point), which means we can solve system with up to three unknowns. If a 2D system has 3 or less unknown reaction forces, it is considered determinate. If it has more than three unknown reaction forces, it is considered indeterminate.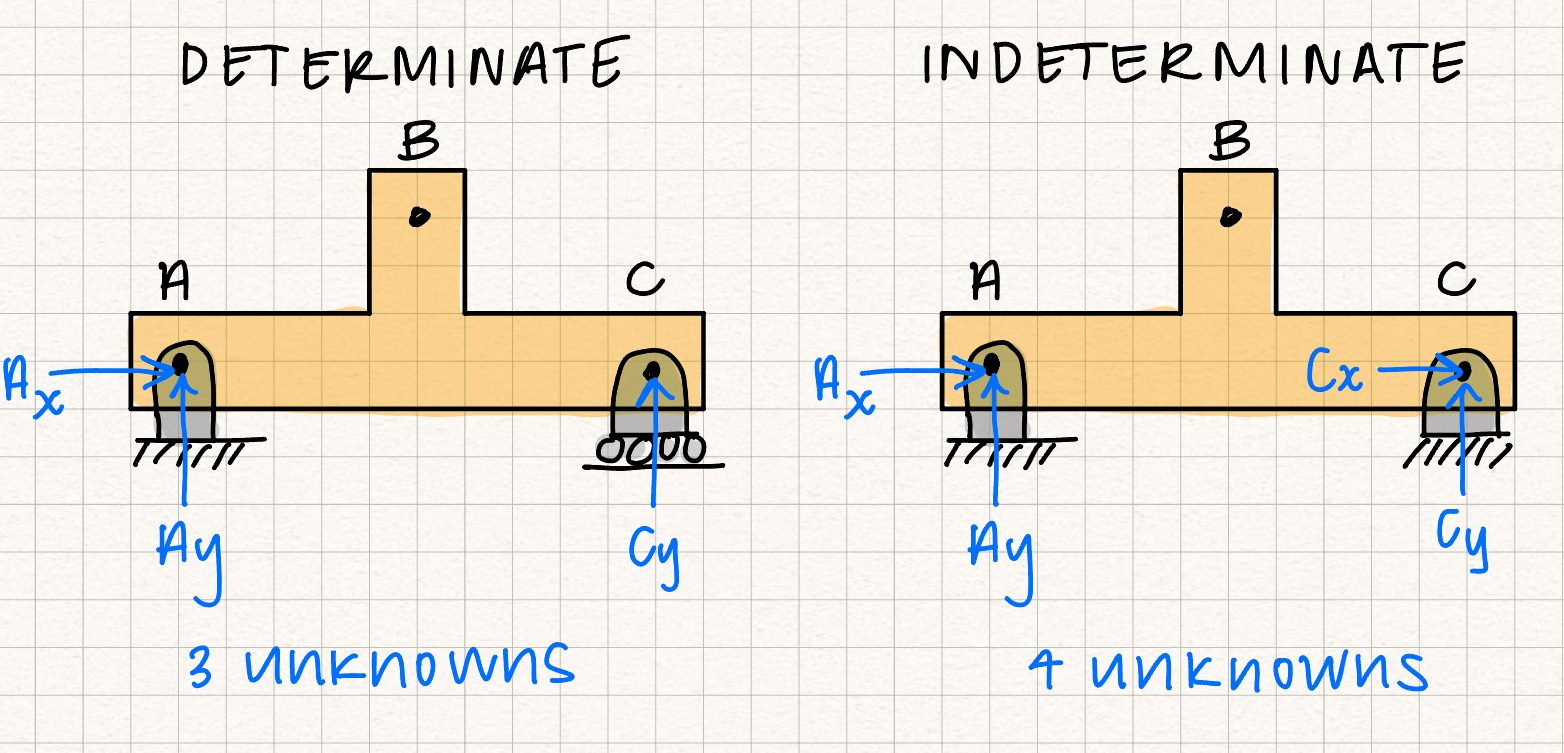
Heads up!
Truss determinacy and stability builds on this content later in the course.
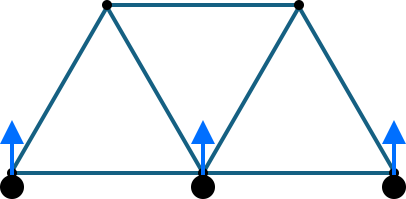
All reactions forces being parallel is an example of improper constraints.
Proper and improper constraints
A system can be properly or improperly constrained under different loading conditions. A system is considered properly constrained when there is a unique solution to the problem of determining support reactions. If there are multiple solutions to the problem, then the system is considered properly constrained with redundancy. If there is no solution, the system is considered to be improperly constrained for those specific loading conditions.Stability and instability
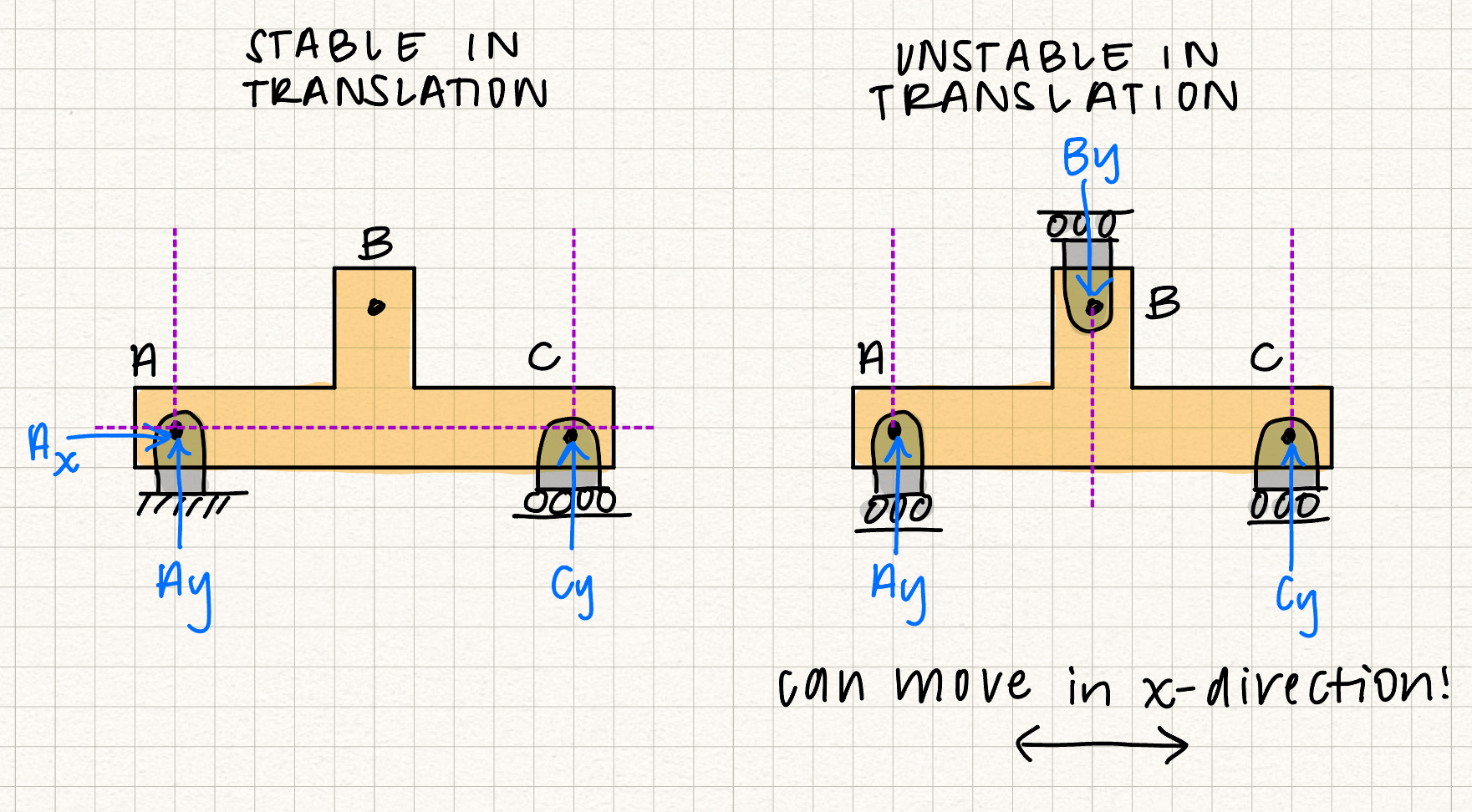
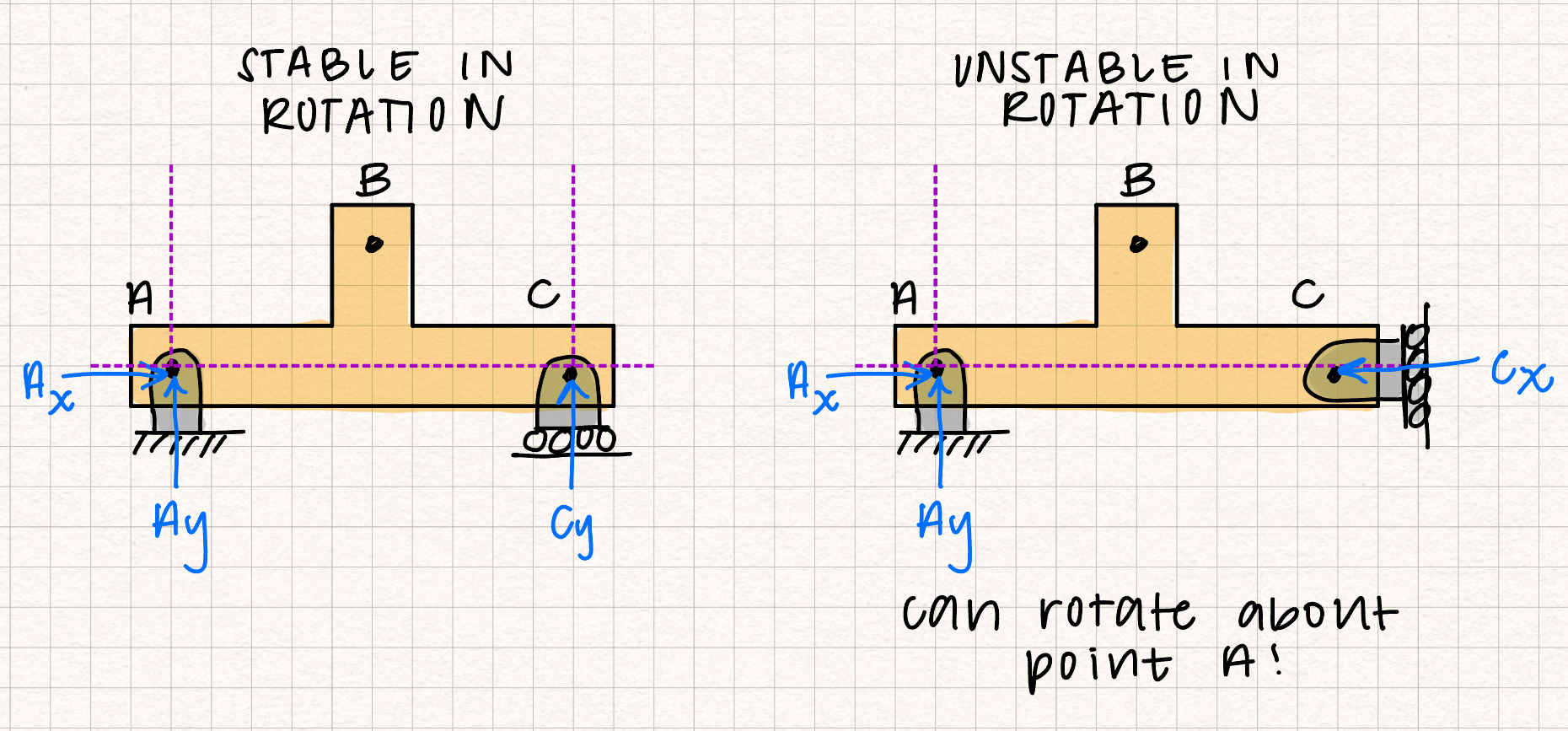
If a system is stable in statics, it means that it cannot rotate or translate in any direction under any loading conditions. There are three ways we can analyze a 2D system to determine if it is stable or unstable:- If there are less than three reaction forces, the system is unstable and considered "underconstrained".
- If all of the reaction forces have lines of action that are parallel to each other, the system is unstable for translation. Nothing is preventing the system from moving perpendicular to those lines.
- If all of the reaction forces have lines of action that meet in a single point, nothing is preventing the system from rotating about that point and the system is unstable for rotation at that point.