Reference Pages
Mechanical Engineering

    Scroll back to top

    Geometric Properties

    Cross Sectional Area

    Cross sectional area is the area of the face created by slicing through an object or geometry. The dimensions are \( length^2 \), with some common units being \( mm^2 \) or \( in^2 \).

    First Moment of Area: Centroid of an Area

    The first moment of the area A with respect to the z-axis is given by \( Q_x = \int_A y dA = \Sigma yA \) . The first moment of the area A with respect to the y-axis is given by \( Q_y = \int_A x dA = \Sigma zA \). \( (\overline{x}, \overline{y}) \)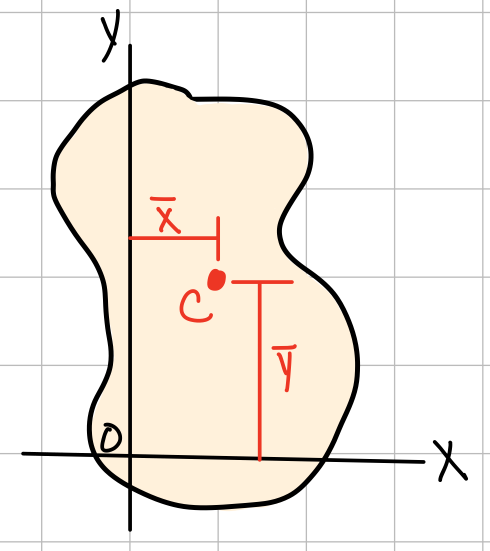
    Centroid of a body
    x coordinate.
    $$ \bar{x} = \frac{1}{A}\int_A x dA\ $$
    y coordinate.
    $$ \bar{y} = \frac{1}{A}\int_A y dA\ $$
    Complex (or composite) areas can be divided into smaller, easier parts.
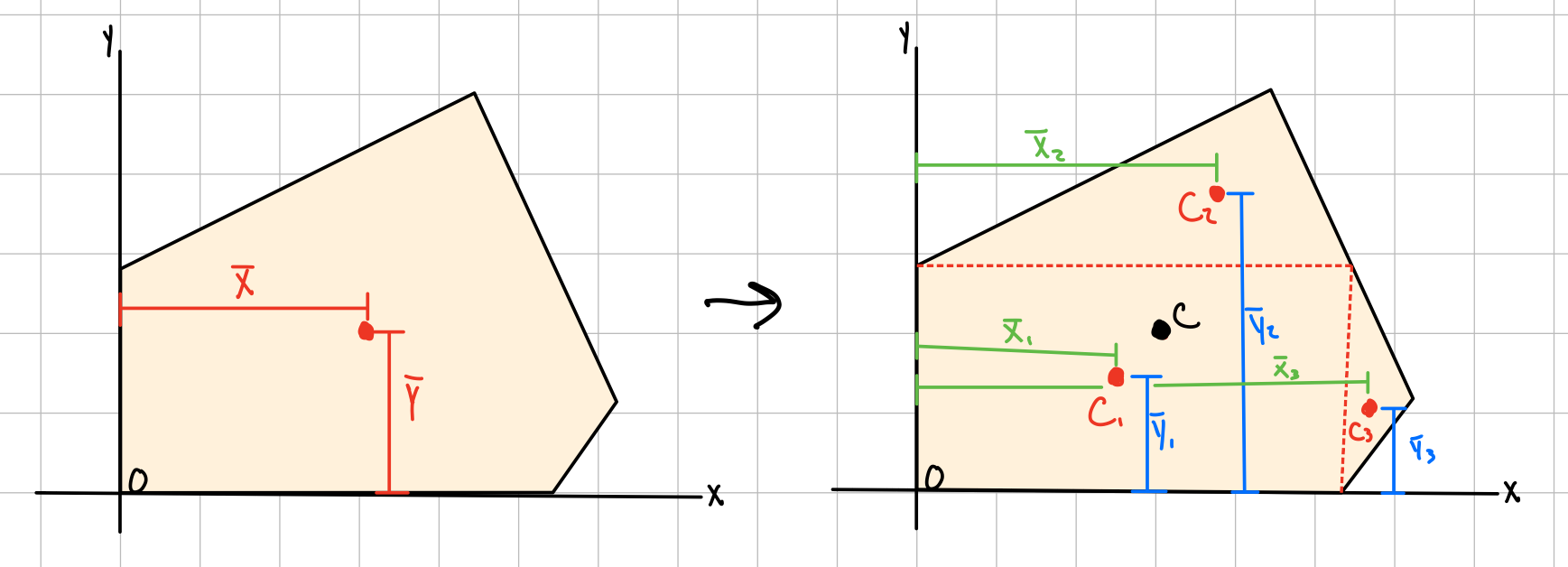
    Centroid of a composite body
    Composite x coordinate
    $$ \bar{X} = \frac{1}{A_{tot}}\sum_i (A_i\bar{y}_i)\ $$
    Composite y coordinate
    $$ \bar{Y} = \frac{1}{A_{tot}} \sum_i (A_i\bar{y}_i) $$

    Second Moment or Area Moment of Inertia

    The moment of inertia of the area \( A \) with respect to the x-axis.
    x-axis second moment.
    $$ I_x = \int_A y^2 dA $$
    The moment of inertia of the area \( A \) with respect to the y-axis.
    y-axis second moment.
    $$ I_y = \int_A x^2 dA $$

    Note: polar moment of inertia in this plane
    Polar moment of Inertia.
    $$ J = \int_A \rho^2 dA = \int_A (y^2 + x^2)dA = I_y + I_x\ $$
    Parallel-axis theorem: the moment of inertia about an axis through C parallel to the axis through the centroid C is related to \( I_C \).
    Parallel axis theorem.
    $$ I_C = I_{C'} +A'd_{CC'}^2\ $$

    Polar Moment of Inertia

    Solid shaft (radius and diameter). #tor-pmi
    $$ J = \frac{\pi R^4}{2} = \frac{\pi D^4}{32} $$
    $$ \begin{aligned}J &= \int_A{\rho^2dA}\\ &= \int_{0}^{2\pi}{\int_0^R{\rho^2(\rho \; d\rho \; d\theta)}}\\ &= \int_{0}^{2\pi}{d\theta}\int_0^R{\rho^3d\rho}\\ &= 2\pi\left[\frac{1}{4} \rho^4\right]_0^R\\ &= \frac{\pi R^4}{2} = \frac{\pi D^4}{32} \end{aligned} $$
    Hollow shaft (inner and outer radius). #tor-hol
    $$ J = \frac{\pi}{2}(R_o^4-R_i^4) = \frac{\pi}{32}(D_o^4-D_i^4)\ $$
    $$ \begin{aligned}J &= \int_{0}^{2\pi}{\int_{R_i}^{R_o}{\rho^3 \; d\rho \; d\theta}} \\ &= \frac{\pi}{2} [{R_o}^4 - {R_i}^4]\end{aligned} $$

    Moment of inertia for typical shapes

    Common shapes about the origin: \( I \) and \( J_O \)
    Common shapes about the centroid: \( \bar{I} \) and \( J_c \)
    Shape Diagram Equations
    Rectangle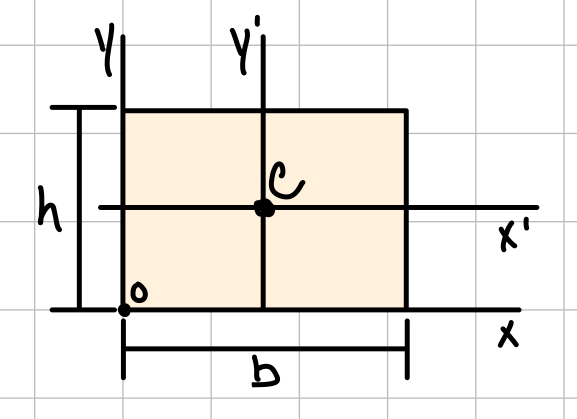
    		\( \bar{I}_{x'} = \frac{1}{12}b h^3 \)

    \( \bar{I}_{y'} = \frac{1}{12}b^3 h \)

    \( I_x = \frac{1}{3}b h^3 \)

    \( I_y = \frac{1}{3}b^3 h \)

    \( J_c = \frac{1}{12}bh(b^2+h^2) \)
    Triangle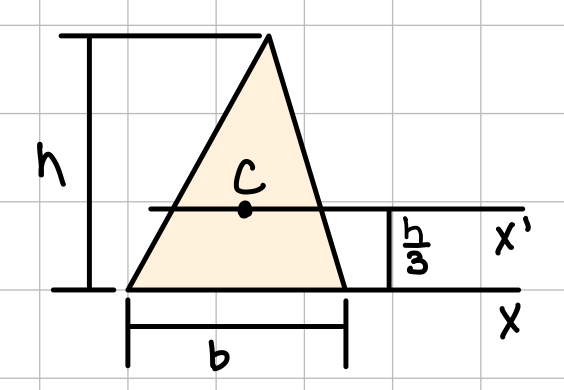
    		\( \bar{I}_{x'} = \frac{1}{36}bh^3 \)

    \( I_x = \frac{1}{12}bh^3 \)
    Circle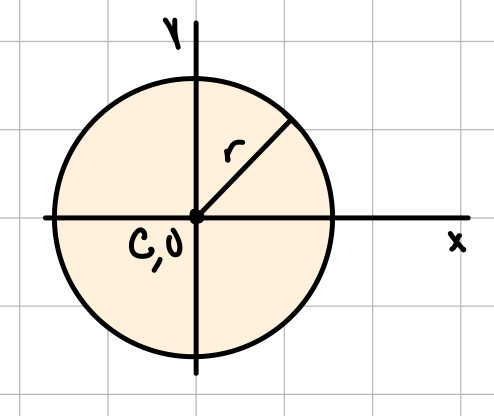
    		\( \bar{I}_x = \bar{I}_y = \frac{1}{4} \pi r^4 \)

    \( J_O= \frac{1}{2} \pi r^4 \)
    Semicircle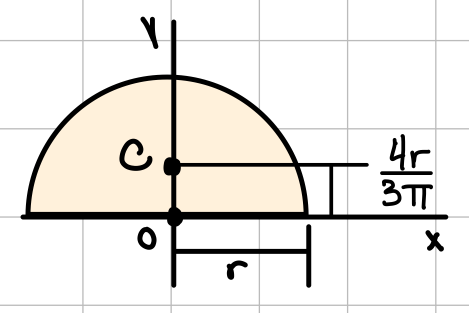
    		\( I_x = I_y = \frac{1}{8} \pi r^4 \)

    \( J_O = \frac{1}{4} \pi r^4 \)
    Quarter circle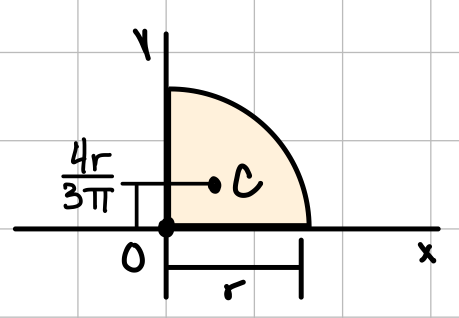
    		\( I_x = I_y = \frac{1}{16} \pi r^4 \)

    \( J_O = \frac{1}{8} \pi r^4 \)
    Ellipse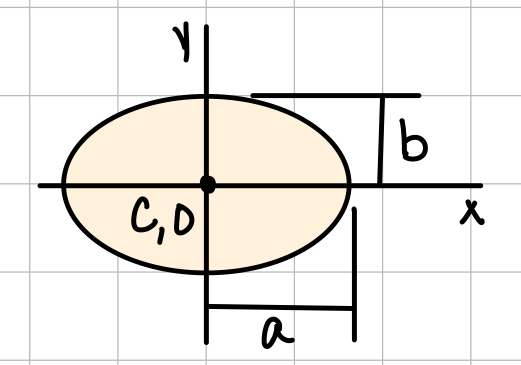
    		\( \bar{I}_x = \frac{1}{4} \pi a b^3 \)

    \( \bar{I}_y = \frac{1}{4} \pi a^3 b \)

    \( J_O = \frac{1}{4} \pi ab(a^2+b^2) \)

    Summary: moment of inertia

    Mass moment of inertia Area moment of inertia (used in solid mechanics!)
    Other names First moment of area Second moment of area Polar moment of area
    Description Determines the torque needed to produce a desired angular rotation about an axis of rotation (resistance to rotation) Determines the centroid of an area Determines the moment needed to produce a desired curvature about an axis(resistance to bending) Determines the torque needed to produce a desired twist a shaft or beam(resistance to torsion)
    Equations
    $$ I_{P,\hat{a}} = \iiint_\mathcal{B} \rho r^2 \,dV\ $$
    $$ Q_z = \int_A y dA = \Sigma yA $$
    $$ Q_y = \int_A z dA = \Sigma zA $$
    $$ \bar{y} = \frac{1}{A}\int_A y dA $$
    $$ \bar{z} = \frac{1}{A}\int_A z dA $$
    $$ I_x = \int_{A}^{} y^2 \,dA \ $$
    $$ I_y = \int_{A}^{} x^2 \,dA \ $$
    $$ \begin{aligned} J_O &= \int_{A}^{} r^2 \,dA \\ &= \int_{A}^{} (x^2+y^2) \,dA\ \end{aligned} $$
    Units \( \mathrm{mass} \ \mathrm{length} ^ 2 \) \( \mathrm{length} ^ 3 \) \( \mathrm{length} ^ 4 \) \( \mathrm{length} ^ 4 \)
    Typical Equations
    $$ \tau = I\alpha $$
    $$ \tau = \frac{VQ}{It} $$
    $$ \sigma = \frac{My}{I} $$
    $$ \tau = \frac{VQ}{It} $$
    $$ \tau = \frac{T\rho}{J} $$
    Courses Dynamics Solid mechanics Statics, solid mechanics Solid mechanics

    Review?

    Need a review of moment of inertia (second moment of area)?

    This content has also been in statics.

    The second moment of area determines the moment needed to produce a desired curvature about an axis (resistance to bending).