Reference Pages
Mechanical Engineering

    Scroll back to top

    Particle kinematics

    The two basic geometric objects we are using are positions and vectors. Positions describe locations in space, while vectors describe length and direction (no position information). To describe the kinematics (motion) of bodies we need to relate positions and vectors to each other.

    Position vectors

    Two positions P and Q can be used to define a vector \( \vec{r}_{PQ} = \vec{PQ} \) from P to Q. We call this the relative position of Q from P. If we start from the origin O, so we have \( \vec{r}_{OP} = \vec{OP} \), then we call this the position vector of position P. When it is clear, we will write \( \vec{r}_P \) for this position vector, or sometimes even just \( \vec{r} \).

    Points \(P\) and \(Q\) and their relative and absolute position vectors. Note that we can write the position vectors with respect to different origins and in different bases.

    Heads up!

    Similar to particle kinematics, rigid body kinematics also builds on this content later in the course.

    Rigid body kinematics examines the velocity and acceleration of particles on the same rigid body.

    Transformation of position vectors

    The position vector \( \vec{r}_{OP} \) a point P depends on which origin we are using. Using a different origin will result in a different position vector for the same point. The position vectors of a point from two different origins differ by the offset vector between the origins:

    Change of origin for position vectors. #rkv-eo
    $$ \begin{aligned} \overrightarrow{O_1 P} &= \overrightarrow{O_1 O_2} + \overrightarrow{O_2 P} \\ \vec{r}_{O_1 P} &= \vec{r}_{O_1 O_2} + \vec{r}_{O_2 P} \end{aligned} $$

    Position vectors are defined by the origin and the point, but not by any choice of basis. We can write any position vector in any basis and it is still the same vector.

    Basis for \( \vec{r}_{O_1P} \):

    none \( \hat\imath,\hat\jmath \) \( \hat{u},\hat{v} \)

    Basis for \( \vec{r}_{O_1P} \):

    none \( \hat\imath,\hat\jmath \) \( \hat{u},\hat{v} \)

    Velocity and acceleration vectors

    The velocity \( \vec{v} \) and acceleration \( \vec{a} \) are the first and second derivatives of the position vector \( \vec{r} \). Technically, this is the velocity and acceleration relative to the given origin, as discussed in detail in the sections on relative motion and frames.

    Definition of velocity and acceleration. #rkv-ev
    $$ \begin{aligned} \vec{v} &= \dot{\vec{r}}\\ \vec{a} &= \dot{\vec{v}} \end{aligned} $$

    The velocity can be decomposed into components parallel and perpendicular to the position vector, reflecting changes in the length and direction of \( \vec{r} \).

    Decomposition of velocity and acceleration vectors. #rkv-ec
    $$ \begin{aligned} \vec{v}_{proj} &= Proj(\vec{v}, \vec{r}) = \dot{r}\hat{r} \\ \vec{v}_{comp} &= Comp(\vec{v}, \vec{r}) = r\dot{\hat{r}} \\ \vec{a}_{proj} &= Proj(\vec{a}, \vec{v}) = \dot{v}\hat{v} \\ \vec{a}_{comp} &= Comp(\vec{a}, \vec{v}) = v\dot{\hat{v}} \end{aligned} $$

    Show:
    Movement: circle var-circle ellipse arc
    trefoil eight comet pendulum
    Show:

    Velocity and acceleration of various movements. Compare to Figure #rvc-fp.

    Velocity and acceleration in Cartesian basis

    Differentiating in a fixed Cartesian basis can be done by differentiating each component.

    Velocity and acceleration in cartesian basis. #rkv-er
    $$ \begin{aligned} \vec{r} &= r_1 \hat\imath + r_2 \hat\jmath + r_3 \hat{k} \\ \vec{v} &= \dot{r}_1 \hat\imath + \dot{r}_2 \hat\jmath + \dot{r}_3 \hat{k} \\ \vec{a} &= \ddot{r}_1 \hat\imath + \ddot{r}_2 \hat\jmath + \ddot{r}_3 \hat{k} \end{aligned} $$

    Velocity and acceleration in polar basis

    Computing velocity and acceleration in a polar basis must take account of the fact that the basis vectors are not constant.

    Velocity and acceleration in polar basis. #rkv-ep
    $$ \begin{aligned} \vec{r} &=r\hat{e}_{r} \\ \vec{v} &=\dot{r}\hat{e}_{r} + r\dot{\theta}\hat{e}_{\theta} \\ \vec{a} &=(\ddot{r} - r\dot{\theta}^2)\hat{e}_{r} + (r\ddot{\theta} + 2 \dot{r}\dot{\theta})\hat{e}_{\theta} \end{aligned} $$

    The acceleration term \( -r \dot{\theta}^2 \hat{e}_r \) is called the centripetal (center-seeking) acceleration, while the \( 2\dot{r} \dot{\theta} \hat{e}_{\theta} \) term is called the Coriolis acceleration.

    Movement: circle var-circle ellipse arc
    trefoil eight comet pendulum
    Show:
    Origin: \(O_1\) \(O_2\)

    Velocity and acceleration in the polar basis. Compare to Figure #rkv-fa. Observe that \( \hat{e}_r,\hat{e}_\theta \) are not related to the path (not tangent, not in the direction of movement), but rather are defined only by the position vector. Note also that the polar basis depends on the choice of origin.

    Summary table

    Cartesian Polar
    Position
    $$ \vec{r} = x\hat\imath + y \hat\jmath $$
    $$ \vec{r} = r \hat{e}_r $$
    Velocity
    $$ \vec{v} = \dot{x}\hat\imath + \dot{y} \hat\jmath $$
    $$ \vec{v} = \dot{r} \hat{e}_r + r\dot{\theta}\hat{e}_\theta $$
    Acceleration
    $$ \vec{a} = \ddot{x}\hat\imath + \ddot{y} \hat\jmath $$
    $$ \vec{a} = \frac{d}{dt} (\vec{v}) = \ddot{r} \hat{e}_r + \dot{\hat{e}_r} + \dot{r}\dot{\theta}\hat{e}_\theta\ + r\ddot{\theta}\hat{e}_\theta + r\dot{\theta}\dot{\hat{e}_\theta} $$
    $$ \vec{a} = (\ddot{r} - r\dot{\theta}^2 ) \hat{e}_r + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \hat{e}_\theta $$

    Heads up!

    Position velocity acceleration builds on this content in Mechanism design.

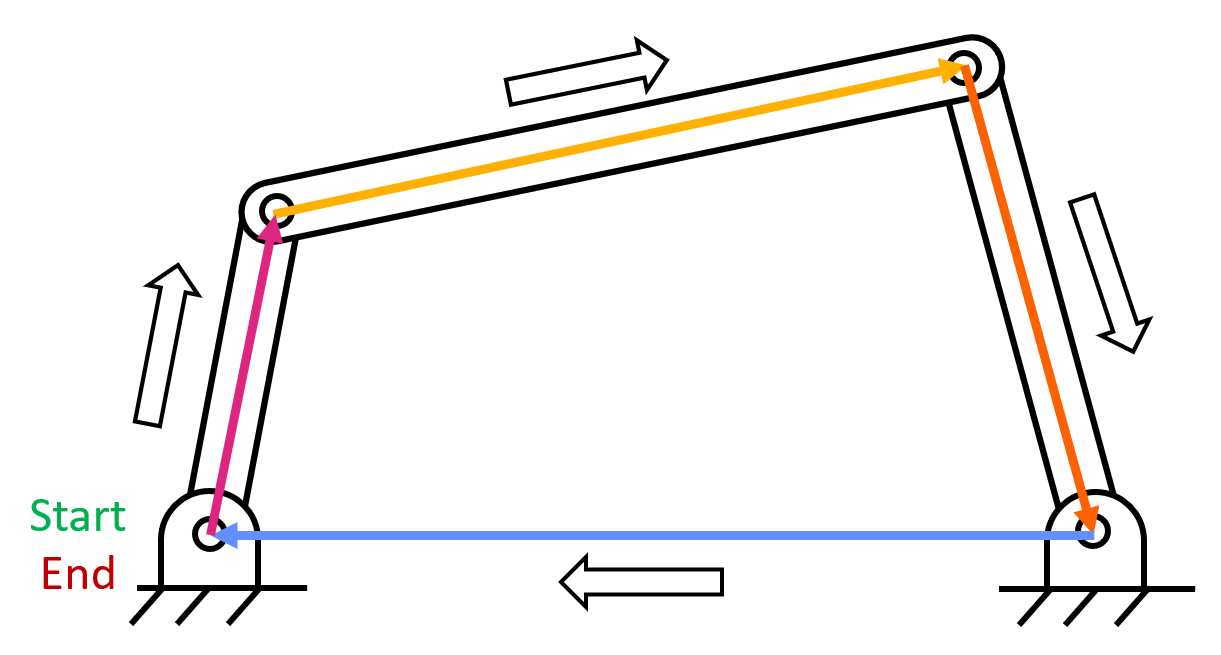
    Position, Velocity, Acceleration (PVA) analysis is used to analytically determine the motion of a mechanism. Position determines the configuration of the mechanism, velocity determines the kinetic energy and momentum, and acceleration determines the forces. The known geometry, initial configurations, and PVA data of one link determines the PVA data for the other links.

    Rotating frames

    Angular velocity

    A rotation of a vector is a change which only alters the direction, not the length, of a vector. A rotation consists of a rotation axis and a rotation rate. By taking the rotation axis as a direction and the rotation rate as a length, we can write the rotation as a vector, known as the angular velocity vector \( \vec{\omega} \). We use the right-hand rule to describe the direction of rotation. The units of \( \vec{\omega} \) are \(\rm rad/s\) or \( {}^\circ/s \).

    Rotation axis: \( \hat\imath \) \( \hat\jmath \) \( \hat{k} \) \( \hat\imath + \hat\jmath \) \( \hat\imath + \hat\jmath + \hat{k} \)

    Angular velocity vector \(\vec\omega\). The direction of \(\vec\omega\) is the axis of rotation, while the magnitude is the speed of rotation (positive direction given by the right-hand rule).

    If an object is rotating with angular velocity \( \omega \) about a fixed origin, then the velocity and acceleration are given by the following relations:

    Velocity and acceleration about a fixed origin. #rkv-ef
    $$ \begin{aligned} \vec{v} &= \vec{\omega} \times \vec{r} \\ \vec{a} &= \vec{\alpha} \times \vec{r} + \vec{\omega} \times (\vec{\omega} \times \vec{r}) \end{aligned} $$

    Did you know?

    The Greek letter ω (lowercase omega) is the last letter of the Greek alphabet, leading to expressions such as “from alpha to omega” meaning “from start to end”. Omega literally means O-mega, meaning O-large, as capital Omega (written Ω) developed from capital Omicron (written Ο) by breaking the circle and turning up the edges. Omicron is literally O-micron, meaning O-small, and it is the ancestor of the Latin letter O that we use today in English.

    Ααalpha Ιιiota Ρρrho
    Ββbeta Κκkappa Σσsigma
    Γγgamma Λλlambda Ττtau
    Δδdelta Μμmu Υυupsilon
    Εεepsilon Ννnu Φφphi
    Ζζzeta Ξξxi Χχchi
    Ηηeta Οοomicron Ψψpsi
    Θθtheta Ππpi Ωωomega

    The Greek alphabet, shown above, was the first true alphabet, meaning that it has letters representing phonemes (basic significant sounds) and includes vowels as well as consonants. The Greek alphabet was was derived from the earlier Phoenician alphabet, which was probably the original parent of all alphabets. This shows that the idea of an alphabet is so non-obvious that it has only ever been invented once, and then always copied after that.

    Vector derivatives and rotations

    If a unit vector \( \hat{a} \) is rotating, then the angular velocity vector \( \vec{\omega} \) is defined so that:

    Derivative of unit vectors. #rkr-ew
    $$ \dot{\hat{a}} = \vec{\omega} \times \hat{a} $$
    Derivative of general vectors. #rkr-ed
    $$ \begin{aligned}\dot{\vec{a}} = \underbrace{\dot{a}\hat{a}}_{\operatorname{Proj}(\dot{\vec{a}}, \vec{a})} +\underbrace{\vec{\omega} \times\vec{a}}_{\operatorname{Comp}(\dot{\vec{a}}, \vec{a})}\end{aligned} $$

    Using the same approach as #rvc-em we write \( \vec{a} =a\hat{a} \) and differentiate this and use rkr-ew to find:

    $$ \begin{aligned}\dot{\vec{a}} &= \frac{d}{dt} \big( a \hat{a} \big) \\&= \dot{a} \hat{a} + a \dot{\hat{a}} \\&= \dot{a} \hat{a} + a (\vec\omega \times \hat{a}) \\&= \dot{a} \hat{a} + \vec\omega \times (a \hat{a}) \\&= \dot{a} \hat{a} + \vec\omega \times \vec{a}.\end{aligned} $$
    Comparing this to #rvc-em shows that the two components are the projection and the complementary projection, respectively.

    Derivative of constant-length vectors. #rkr-el
    $$ \dot{\vec{a}} = \vec{\omega} \times \vec{a}\qquad\text{if \(\vec{a}\) is constant length}\ $$

    This can be seen from the fact that \( \dot{a} = 0 \) if \(a\) is constant (a fixed length vector), substituted into #rkr-ed.

    Rotations in 2D

    In 2D the angular velocity can be thought of as a scalar (positive for counter-clockwise, negative for clockwise). This scalar is just the out-of-plane component of the full angular velocity vector. We can draw the angular velocity as either a vector pointing out of the plane, or as a circle-arrow in the plane, which is simpler for 2D diagrams.

    Show:

    Comparison of the vector and scalar representations of \(\vec\omega\) for 2D rotations.

    In 2D the angular velocity scalar \(\omega\) is simply the derivative of the rotation angle \(\theta\) in the plane:

    Magnitude \(\omega\) is derivative of angle \(\theta\) in 2D. #rkr-e2
    $$ \omega = \dot\theta $$

    Take \( \hat{a} \) to be a unit vector rotating in the 2D \( \hat\imath–\hat\jmath \) plane, making an angle of \(\theta\) with the \(x\)-axis, as in Figure #rkr-f2. Then:

    $$ \hat{a} = \cos\theta \,\hat\imath + \sin\theta \,\hat\jmath. $$
    Differentiating this expression gives:
    $$ \dot{\hat{a}} = -\sin\theta \, \dot\theta \,\hat\imath+ \cos\theta \,\dot\theta \,\hat\jmath. $$
    We now consider an angular velocity vector \(\vec\omega\). Because the rotation is in the \(\hat\imath\)–\(\hat\jmath\) plane, the angular velocity vector must be in the \( \hat{k} \) direction. Thus \( \vec\omega = \omega \hat{k} \). Now we can compute the derivative of \( \hat{a} \) using #rkr-ew, giving:
    $$ \begin{aligned}\dot{\hat{a}} &= \vec\omega \times \hat{a} \\&= \omega\hat{k} \times \big( \cos\theta \,\hat\imath+ \sin\theta \,\hat\jmath \big) \\&= \omega \cos\theta \,(\hat{k} \times \hat\imath)+ \omega \sin\theta \,(\hat{k} \times \hat\jmath) \\&= \omega \cos\theta \,\hat\jmath+ \omega \sin\theta \,(-\hat\imath) \\&= - \omega \sin\theta \,\hat\imath+ \omega \cos\theta \,\hat\jmath.\end{aligned} $$
    Comparing this expression to the earlier one for \( \dot{\hat{a}} \)we see that \(\omega = \dot\theta\).

    The right-hand rule convention for angular velocities means that counter-clockwise rotations are positive, just like the usual angle direction convention.

    Did you know?

    Angular directions have long been considered to have magical or spiritual significance. In Britain the counterclockwise direction was once known as widdershins, and it was considered unlucky to travel around a church in a widdershins direction.

    Interestingly, right-handed people tend to naturally draw circles in a counterclockwise direction, and clockwise drawing in right-handed children is an early warning sign for the later development of schizophrenia [Blau, 1977].

    References

    • T. H. Blau. Torque and schizophrenic vulnerability. American Psychologist, 32(12):997–1005, 1977. DOI: 10.1037/0003-066X.32.12.997.

    Rotations and vector “positions”

    The fact that vectors don't have positions means that vector rotations are independent of where vectors are drawn, just like for derivatives.

    Show:

    Rotational motion of vectors which are drawn moving about. Note that the drawn position does not affect the angular velocity $\omega$ or the derivative vectors.

    Properties of rotations

    Rotations are rigid transformations, meaning that they keep constant all vector lengths and all relative vector angles. These facts are reflected in the following results, which all consider two vectors \( \vec{a} \) and \( \vec{b} \) that are rotating with angular velocity \( \vec\omega \).

    Derivative of rotating vector is orthogonal. #rkr-e2a
    $$ \dot{\vec{a}} \cdot \vec{a} = 0 $$

    Using #rkr-el and the scalar triple product formula #rvi-es gives:

    $$ \begin{aligned}\vec{a} \cdot \dot{\vec{a}}&= \vec{a} \cdot \big( \vec{\omega} \times \vec{a} \big) \\&= \vec{\omega} \cdot \big( \vec{a} \times \vec{a} \big) \\&= 0.\end{aligned} $$

    Angle \(\theta\) between rotating vectors is constant. #rkr-e2b
    $$ \theta = \cos^{-1}\left(\frac{\vec{b} \cdot\vec{a}}{b a}\right) = \text{constant} $$

    We first consider the dot product \( \vec{a} \cdot \vec{b} \) and show that this is not changing with time. We do this by using the scalar triple product formula #rvi-es to find:

    $$ \begin{aligned}\frac{d}{dt} \big( \vec{a} \cdot \vec{b} \big)&= \dot{\vec{a}} \cdot \vec{b} + \vec{a} \cdot \dot{\vec{b}} \\&= (\vec{\omega} \times \vec{a}) \cdot \vec{b} + \vec{a} \cdot (\vec{\omega} \times \vec{b}) \\&= \vec{b} \cdot (\vec{\omega} \times \vec{a}) + \vec{b} \cdot (\vec{a} \times \vec{\omega}) \\&= \vec{b} \cdot (\vec{\omega} \times \vec{a}) - \vec{b} \cdot (\vec{\omega} \times \vec{a}) \\&= 0.\end{aligned} $$
    Now \( \vec{a} \cdot \vec{b} \) is constant and the lengths \(a\) and \(b\) are constant, so the angle \(\theta\) between the vectors must be constant.

    Rotating vectors parallel to \(\vec\omega\) are constant. #rkr-e2c
    $$ \dot{\vec{a}} = 0 \qquad \text{if \(\vec{a}\) is rotating and parallel to \(\vec\omega\)} $$

    From #rkr-el we know that the derivative is

    $$ \dot{\vec{a}} = \vec\omega \times \vec{a}, $$
    but the cross product is zero for parallel vectors, so this the derivative is zero.

    Rodrigues’ rotation formula

    Rodrigues’ rotation formula gives an explicit formula for a vector rotated by an angle about a given axis.

    Rodrigues’ rotation formula for \(\vec{a}\) rotated by \(\theta\) about \(\hat{b}\). #rkr-er
    $$ \operatorname{Rot}(\vec{a}; \theta, \hat{b}) =\vec{a} \cos\theta + (\hat{b} \times\vec{a}) \sin\theta + \hat{b} (\hat{b} \cdot\vec{a}) (1 - \cos\theta) $$

    Assume \( \vec{a} \) is not parallel to \( \hat{b} \). Then let \( \vec{v} = \hat{b} \times \vec{a} \) and \( \vec{u} = \vec{v} \times \vec{b} \), so \( \hat{u}, \hat{v}, \hat{b} \) is a right-handed orthonormal basis. Take \(\phi\) to be the angle between \( \vec{a} \) and \( \hat{b} \). Then we do a rotation by \(\theta\) in the \( \hat{u}-\hat{v} \) plane:

    $$ \begin{aligned} \vec{a} &= a \sin\phi\,\hat{u} + a \cos\phi \,\hat{b} \\\operatorname{Rot}(\vec{a};\theta,\hat{b}) &= a\cos\theta \sin\phi \,\hat{u} + a \sin\theta \sin\phi\,\hat{v} + a \cos\phi \,\hat{b}.\end{aligned} $$

    Now we want to convert from the \( \hat{u},\hat{v},\hat{b} \) basis to write the rotated result in terms of \( \vec{a}, \hat{b} \times \vec{a}), \hat{b} \). To do this, we need to work out what \( \hat{u},\hat{v},\hat{b} \)are in terms of these other vectors.

    $$ \begin{aligned} \hat{v} &= \frac{\hat{b} \times\vec{a}}{\|\hat{b} \times \vec{a}\|} =\frac{\hat{b} \times \vec{a}}{a \sin\phi} \\\hat{u} &= \frac{\vec{v} \times\hat{b}}{\|\vec{v} \times \vec{b}\|} =\frac{\vec{v} \times \hat{b}}{a \sin\phi} =\frac{(\hat{b} \times \vec{a}) \times \hat{b}}{a\sin\phi} = \frac{\hat{b} \times (\vec{a} \times\hat{b})}{a \sin\phi} \\&= \frac{\vec{a} - (\hat{b}\cdot \vec{a}) \hat{b}}{a \sin\phi} = \frac{1}{a\sin\phi} \vec{a} - \frac{\hat{b} \cdot\vec{a}}{a \sin\phi} \hat{b}.\end{aligned} $$

    Substituting these into the rotated vector expression above gives

    $$ \begin{aligned}\operatorname{Rot}(\vec{a};\theta,\hat{b}) &= a\cos\theta \sin\phi \, \left( \frac{1}{a \sin\phi}\vec{a} - \frac{\hat{b} \cdot \vec{a}}{a\sin\phi} \hat{b} \right) \\& \qquad + a \sin\theta \sin\phi \, \left(\frac{\hat{b} \times \vec{a}}{a \sin\phi} \right)+ a \cos\phi \,\hat{b} \\ &= \cos\theta\,\vec{a} - \cos\theta \,(\hat{b} \cdot\vec{a}) \,\hat{b} + \sin\theta \,(\hat{b} \times\vec{a}) + a\cos\theta \,\hat{b} \\ &=\cos\theta \,\vec{a} + (1 - \cos\theta) (\hat{b}\cdot \vec{a}) \,\hat{b} + \sin\theta \,(\hat{b}\times \vec{a}).\end{aligned} $$

    Angular acceleration

    In polar coordinates, acceleration consists of both radial and tangential components. The tangential component is directly related to changes in the angular velocity, which introduces the concept of angular acceleration.

    Angular acceleration, denoted as \( \ddot{\theta} \) represents the rate of change of angular velocity \( \dot{\theta} \) with respect to time. It appears as part of the total acceleration in the tangential direction, described by the unit vector \( \hat{e}_{\theta} \). The full expression for the acceleration in polar coordinates is:

    $$ \vec{a} = (\ddot{r} - r\dot{\theta}^2) \hat{e}_r + (r\ddot{\theta} + 2\dot{r}\dot{\theta}) \hat{e}_\theta $$

    Here, the first term of the equation represents the radial component, described by the unit \( \hat{e}_r \), and the second term is the angular component, described by the vector unit \( \hat{e}_{\theta} \). In the radial component, there is a radial (\( \ddot{r} \)) and a centripetal (\( r\dot{\theta}^2 \)) term. In the angular component, there is an angular (\( r\ddot{\theta} \)) and a coriolis (\( 2\dot{r}\dot{\theta} \)) term.

    Tangential and normal basis

    Normal basis

    Consider a particle moving with position vector \( \vec{r} \) and corresponding velocity \( \vec{v} \) and acceleration \( \vec{a} \). The tangential/normal basis \( \hat{e}_t,\hat{e}_n,\hat{e}_b \) is:

    Tangential/normal basis vectors. #rkt-eb
    $$ \begin{aligned}\hat{e}_t &= \hat{v}& &\text{tangential basis vector} \\\hat{e}_n &= \frac{\dot{\hat{e}}_t}{\|\dot{\hat{e}}_t\|}= \frac{\operatorname{Comp}(\vec{a},\vec{v})}{\|\operatorname{Comp}(\vec{a},\vec{v})\|}& &\text{normal basis vector} \\\hat{e}_b &= \hat{e}_t \times \hat{e}_n& &\text{binormal basis vector} \\\end{aligned} $$

    These equations are definitions of the basis vectors, so the only thing to derive is the alternative formula for \( \hat{e}_n \). Using the definition of \( \hat{e}_t \) above and #rvc-eu, we see that

    $$ \dot{\hat{e}}_t = \dot{\hat{v}} = \frac{1}{v} \operatorname{Comp}(\dot{\vec{v}}, \vec{v}) = \frac{1}{v} \operatorname{Comp}(\vec{a}, \vec{v}). $$
    Normalizing both sides gives the desired expression:
    $$ \frac{\dot{\hat{e}}_t}{\|\dot{\hat{e}}_t\|} = \frac{\frac{1}{v} \operatorname{Comp}(\vec{a}, \vec{v})}{ \left\|\frac{1}{v} \operatorname{Comp}(\vec{a}, \vec{v})\right\|} = \frac{\frac{1}{v} \operatorname{Comp}(\vec{a}, \vec{v})}{ \frac{1}{v} \|\operatorname{Comp}(\vec{a}, \vec{v})\|} = \frac{\operatorname{Comp}(\vec{a}, \vec{v})}{ \|\operatorname{Comp}(\vec{a}, \vec{v})\|}. $$

    The tangential basis vector \( \hat{e}_t \) points tangential to the path, the normal basis vector \( \hat{e}_n \) points perpendicular (normal) to the path towards the instantaneous center of curvature, and the binormal basis vector \( \hat{e}_b \) completes the right-handed basis.

    Show:

    Tangential/normal basis associated with movement around a curve in 3D. Observe that the velocity \( \vec{v} \) is always in the \( \hat{e}_t \) direction and that the acceleration \( \vec{a} \) always lies in the \( \hat{e}_t,\hat{e}_n \) plane (the osculating plane). The center of curvature and osculating circle are defined below.

    Curvature and torsion

    Curvature and torsion. #rkt-ek

    To better understand the geometry of the tangential/normal basis, we can use the curvature \(\kappa\) to describe the curving of the path, and the torsion \(\tau\) to describe the rotation of the basis about the path. These quantities are defined by:

    $$ \begin{aligned}\kappa &= \frac{d\hat{e}_t}{ds} \cdot \hat{e}_n= \frac{1}{v} \dot{\hat{e}}_t \cdot \hat{e}_n & &\text{curvature} \\\rho &= \frac{1}{\kappa} & &\text{radius of curvature} \\\tau &= -\frac{d\hat{e}_b}{ds} \cdot \hat{e}_n= -\frac{1}{v} \dot{\hat{e}}_b \cdot \hat{e}_n & &\text{torsion} \\\sigma &= \frac{1}{\tau} & &\text{radius of torsion}\end{aligned} $$

    These equations are definitions, so we need only check that the two expressions for each of \(\kappa\) and \(\tau\) are equivalent. This follows immediately, however, from the chain-rule conversions #rkt-ea between \(d/ds\) and \(d/dt\).

    The radius of curvature \(\rho\) is the radius of equivalent circular motion, and the torsion determines the rate of rotation of the osculating plane, as described below in a section below.

    Basis derivatives and angular velocity

    As the point \(P\) moves along its path, the associated tangential/normal basis rotates with an angular velocity vector \(\omega\) given by:

    Angular velocity of the tangential/normal basis. #rkt-ew
    $$ \begin{aligned}\vec{\omega} &= v\tau \,\hat{e}_t + v \kappa \,\hat{e}_b\end{aligned} $$

    We start by writing the angular velocity in the tangential/normal basis, giving:

    $$ \vec{\omega} = \omega_t\,\hat{e}_t + \omega_n\,\hat{e}_n+ \omega_b\,\hat{e}_b. $$
    Now the basis vector derivatives are given by the cross product by \( \vec{\omega} \) from #rkr-ew, so we can evaluate the expressions #rkt-ek for curvature and torsion to give:
    $$ \begin{aligned}\kappa &= \frac{1}{v} \dot{\hat{e}}_t \cdot \hat{e}_n \\&= \frac{1}{v} (\vec{\omega} \times \hat{e}_t) \cdot \hat{e}_n \\&= \frac{1}{v} (\omega_b\,\hat{e}_n - \omega_n\,\hat{e}_b) \cdot \hat{e}_n \\&= \frac{1}{v} \omega_b\end{aligned} $$
    and
    $$ \begin{aligned}\tau &= -\frac{1}{v} \dot{\hat{e}}_b \cdot \hat{e}_n \\&= -\frac{1}{v} (\vec{\omega} \times \hat{e}_b) \cdot \hat{e}_n \\&= -\frac{1}{v} (\omega_n\,\hat{e}_t - \omega_t\,\hat{e}_n) \cdot \hat{e}_n \\&= \frac{1}{v} \omega_t.\end{aligned} $$
    Rearranging the final expressions in each case gives \( \omega_b = v\kappa \) and \( \omega_t = v\tau \). From the definition #rkt-eb of \( \hat{e}_n \), we see that
    $$ \begin{aligned}\hat{e}_n &= \frac{\dot{\hat{e}}_t}{\|\dot{\hat{e}}_t\|} \\\hat{e}_n \cdot \hat{e}_b &= \frac{1}{\|\dot{\hat{e}}_t\|} (\vec{\omega} \times \hat{e}_t) \cdot \hat{e}_b \\0 &= \frac{1}{\|\dot{\hat{e}}_t\|} (\omega_b\,\hat{e}_n - \omega_n\,\hat{e}_b) \cdot \hat{e}_b \\&= - \frac{1}{\|\dot{\hat{e}}_t\|} \omega_n.\end{aligned} $$
    from which we conclude that \( \omega_n = 0 \), giving us all three components of \( \vec{\omega} \).

    Knowing the angular velocity vector of the tangential/normal basis allows us to easily compute the time derivatives of each tangential/normal basis vector, as follows:

    Tangential/normal basis vector derivatives. #rkt-ed
    $$ \begin{aligned}\dot{\hat{e}}_t &= \phantom{-v\kappa\,\hat{e}_t - } v\kappa\,\hat{e}_n \\\dot{\hat{e}}_n &= -v\kappa\,\hat{e}_t \phantom{ - v\kappa\,\hat{e}_n + } + v\tau\,\hat{e}_b \\\dot{\hat{e}}_b &=\phantom{-v\kappa\,\hat{e}_t } - v\tau\,\hat{e}_n\end{aligned} $$

    We can use the expression #rkt-ew for \( \vec{\omega} \) together with #rkr-ew to find the basis vector derivatives:

    $$ \begin{aligned}\dot{\hat{e}}_t &= \vec{\omega} \times \hat{e}_t= (v\tau \,\hat{e}_t + v \kappa \,\hat{e}_b) \times \hat{e}_t= v \kappa \,\hat{e}_n \\\dot{\hat{e}}_n &= \vec{\omega} \times \hat{e}_n= (v\tau \,\hat{e}_t + v \kappa \,\hat{e}_b) \times \hat{e}_n= - v \kappa \,\hat{e}_t + v \tau \,\hat{e}_b \\\dot{\hat{e}}_b &= \vec{\omega} \times \hat{e}_b= (v\tau \,\hat{e}_t + v \kappa \,\hat{e}_b) \times \hat{e}_b= -v \tau \,\hat{e}_n.\end{aligned} $$

    Notation note

    The tangential/normal basis is also called the Frenet–Serret frame after Jean Frédéric Frenet and Joseph Alfred Serret, who discovered it independently around 1850. The equations #rkt-ed for the basis derivatives are often called the Frenet-Serret formulas, typically written in terms of \(s\) derivatives:

    $$ \begin{aligned}\frac{d\hat{e}_t}{ds} &= \phantom{-\kappa\,\hat{e}_t - } \kappa\,\hat{e}_n \\\frac{d\hat{e}_n}{ds} &= -\kappa\,\hat{e}_t \phantom{ - \kappa\,\hat{e}_n + } + \tau\,\hat{e}_b \\\frac{d\hat{e}_b}{ds} &=\phantom{-\kappa\,\hat{e}_t } - \tau\,\hat{e}_n.\end{aligned} $$

    If we divide the angular velocity vector #rkt-ew by \(v\) then we obtain the vector

    $$ \frac{1}{v} \vec{\omega} = \tau\,\hat{e}_t + \kappa\,\hat{e}_b, $$

    which is known as the Darboux vector after its discoverer, Jean Gaston Darboux.

    Normal and tangential kinematics

    While the motion of a point \(P\) along a path defines the tangential/normal basis, we can also use this basis to express the kinematics of \(P\) itself, giving the following expressions for velocity and acceleration.

    Velocity and acceleration in tangential/normal basis. #rkt-e
    $$ \begin{aligned}\vec{v} &= \dot{s} \, \hat{e}_t \\\vec{a} &= \ddot{s} \, \hat{e}_t + \frac{\dot{s}^2}{\rho} \hat{e}_n\end{aligned} $$

    From the definition #rkt-eb of \( \hat{e}_t \) we see that \( v\,\hat{e}_t = v\hat{v} = \vec{v} \), which is the first equation above. Differentiating this and using \( v = \dot{s} \) from #rkt-es gives

    $$ \begin{aligned}\vec{v} &= \dot{s}\,\hat{e}_t \\\vec{a} = \dot{\vec{v}}&= \ddot{s}\,\hat{e}_t + \dot{s}\,\dot{\hat{e}}_t \\&= \ddot{s}\,\hat{e}_t + \dot{s}(v \kappa \,\hat{e}_n) \\&= \ddot{s}\,\hat{e}_t + \frac{\dot{s}^2}{\rho} \,\hat{e}_n,\end{aligned} $$
    where we used the derivative #rkt-ed of \( \hat{e}_t \) in terms of the curvature \(\kappa\), and the definition #rkt-ek of the radius of curvature to give \( \kappa = 1/\rho \).

    The above formula shows that the normal acceleration component \(a_n\) is determined by the radius of curvature. We can therefore also find the radius of curvature from knowing the normal acceleration:

    Radius of curvature \(\rho\) for velocity \(\vec{v}\) and acceleration \(\vec{a}\) with angle \(\theta\) between them. #rkt-er
    $$ \rho = \frac{v^2}{a_n} = \frac{v^2}{|a\sin\theta|} $$

    From #rkt-ev we known that the normal component of the acceleration is given by \( a_n =\dot{s}^2/\rho \) and from the definition #rkt-es of path length we have \( \dot{s} = v \), so this equation can be rearranged to give \( \rho = v^2 / a_n \).

    Now because \( \vec{a} \) only has \( \hat{e}_t \) and \( \hat{e}_n \) components, the \( \hat{e}_n \) component is given by

    $$ \begin{aligned}a_n &= \|\operatorname{Comp}(\vec{a}, \hat{e}_t)\| \\&= \|\operatorname{Comp}(\vec{a}, \vec{v})\| \\&= |a \sin\theta|,\end{aligned} $$
    where we used the facts that \( \vec{e}_t \) is in the direction of \( \vec{v} \), that \( \operatorname{Comp}(\vec{a},\vec{v}) \) does not depend on the magnitude of \( \vec{v} \), and equation #rvv-em for the magnitude of the complementary projection.

    Movement: circle var-circle ellipse arc
    trefoil eight comet pendulum
    Show:
    Origin: \(O_1\) \(O_2\)

    Velocity and acceleration in the tangential/normal basis. Note that the tangential/normal basis does not depend on the choice of origin or the position vector, in contrast to the polar basis.

    Tangent lines and osculating circles

    Given a point \(P\) moving along a complex path, at a given instant of time we can match different components of the point's motion with successively more complex geometric shapes:

    match geometric object name
    \( \vec{r} \) point position
    \( \vec{r},\vec{v} \) line tangent line
    \( \vec{r},\vec{v},\vec{a} \) circle osculating circle

    The osculating circle is the instantaneous equivalent circular path. That is, a particle traveling on the osculating circle with the same location \(P\), speed \( \dot{s} \), and tangential acceleration \( \ddot{s} \) as our particle would have matching velocity and acceleration vectors.

    Osculating circle #rkt-eo
    $$ \text{center C} = \vec{r} + \rho \hat{e}_n,\qquad \text{radius} \; \rho,\qquad \text{normal to} \; \hat{e}_b $$

    Consider a particle \(P\) with position vector \( \vec{r}_P \) moving with velocity \( \vec{v}_P \) and acceleration \( \vec{a}_P \) , and let \( \hat{e}_t,\hat{e}_n,\hat{e}_b \)be the associated tangential/normal basis and \( \rho_P \) be the radius of curvature. Set \( \dot{s}_P = v_P \)and \( \ddot{s}_P = \vec{a}_P \cdot \hat{e}_t \) to be the speed and tangential acceleration of \(P\).

    Next define the osculating circle as above with center \( C = \vec{r}_P + \rho_P \) , radius \( \rho_P \), and normal vector \( \hat{e}_b \).

    Now take a second particle \(Q\) moving on the osculating circle so that its instantaneous position matches \(P\) and it has the same speed \( \dot{s}_Q = \dot{s}_P \) and tangential acceleration \( \ddot{s}_Q = \ddot{s}_P \). This means that the radius of the circle \( r_Q \) for \(Q\) is matches the osculating circle radius \( \rho_P \), so \( r_Q = \rho_P \).

    We want to prove that \( \vec{v}_Q = \vec{v}_P \) and \( \vec{a}_Q = \vec{a}_P \).

    We will use a polar coordinate system for \(Q\), centered at \(C\) and in the plane with normal vector \( \hat{e}_b \). At the current instant when the particles are at the same position, this means that \( \hat{e}_r = -\hat{e}_n \) and \( \hat{e}_\theta = \hat{e}_t \). Using the circular motion expressions #rke-ec we have that the velocity of \(Q\) is:

    $$ \begin{aligned} \vec{v}_Q &= v_Q \,\hat{e}_\theta \\ &= \dot{s}_Q \,\hat{e}_\theta \\ &= \dot{s}_P \,\hat{e}_t = \vec{v}_P. \\ \end{aligned} $$
    For a particle moving in a circle like \(Q\), the speed is given by \( \dot{s}_Q = v_Q = r_Q \omega_Q \), and differentiating this gives \( \ddot{s}_Q = r_Q \dot{\omega}_Q = r_Q \alpha_Q \). Using this, the acceleration of \(Q\) is:
    $$ \begin{aligned} \vec{a}_Q &= -\frac{v_Q^2}{\rho_Q} \,\hat{e}_r + \rho_Q \alpha_Q \,\hat{e}_\theta \\ &= -\frac{\dot{s}_Q^2}{\rho_Q} \,\hat{e}_r + \ddot{s}_Q \,\hat{e}_\theta \\ &= \frac{\dot{s}_P^2}{\rho_P} \,\hat{e}_n + \ddot{s}_Q \,\hat{e}_t \\ &= \vec{a}_Q. \end{aligned} $$
    We thus see that points \(P\) and \(Q\) have the same instantaneous velocity and acceleration. This also means that the tangential/normal basis computed at this instant for \(Q\) will match that of \(P\).

    The osculating circle lies in the \( \hat{e}_t,\hat{e}_n \) plane, which is thus called the osculating plane. This plane has normal vector \( \hat{e}_b \), and rotates about \( \hat{e}_t \) with a rotation rate determined by the torsion \(\tau\), as we see from the expression #rkt-ed for the derivative of \( \hat{e}_b. \)

    Show:

    Match phase:

    0%

    Tangent lines and osculating circles, showing matching of velocity or velocity and acceleration, respectively.

    Curvature on curves

    Given a parametric curve, its curvature can be directly evaluated with:

    Curvature of parametric curve \(\vec{r}(u)\) in 3D. #rkt-ec
    $$ \kappa = \frac{\|\vec{r}' \times \vec{r}''\|}{\|\vec{r}'\|^3} $$

    Because the tangential/normal basis vectors #rkt-eb are all normalized, it does not matter how fast the point moves along the line. We can thus evaluate the parametric curve as a function of time, giving \( \vec{r}(t) \). Now:

    $$ \begin{aligned}\|\vec{r}'' \times \vec{r}'\| &= \|\vec{a} \times \vec{v}\| \\&= a v \sin\theta \\&= \frac{v^3}{\rho},\end{aligned} $$
    where we used the cross product length formula #rvv-el and equation #rkt-er for the radius of curvature \( \rho \). By definition #rkt-ek the curvature is \( \kappa = 1/\rho \), so
    $$ \begin{aligned}\|\vec{r}'' \times \vec{r}'\|&= v^3 \kappa \\\kappa &= \frac{\|\vec{r}'' \times \vec{r}'\|}{\|\vec{r}'\|^3}.\end{aligned} $$

    While the above formula can be used in 2D by taking the third component to be zero, it can also be written in an explicitly 2D form:

    Curvature of parametric curve \(x = x(u)\), \(y = y(u)\) in 2D. #rkt-e2
    $$ \kappa = \frac{|x''y' - y''x'|}{(x'^2 + y'^2)^{3/2}} $$

    This equation is just #rkt-ec written in explicit 2D coordinates. To see this, we first take the position vector \( \vec{r}(u) \) to be

    $$ \vec{r}(u) = x(u)\,\hat\imath + y(u)\,\hat\jmath. $$
    Now \( r'(u) = \sqrt{(x'(u))^2 + (y'(u))^2} \) and
    $$ \begin{aligned}\vec{r}'' \times \vec{r}'&= (x''\,\hat\imath + y''\,\hat\jmath)\times (x'\,\hat\imath + y'\,\hat\jmath) \\&= (x''y' - y''x')\,\hat{k},\end{aligned} $$
    so evaluating #rkt-ec gives the desired expression.

    We can take this a step further, and obtain an expression for an explicitly defined function.

    Curvature of an explicitly defined function \(y = f(x).\) #rkt-e3
    $$ \kappa = \frac{|y''(x)|}{(1 + y'(x)^2)^{3/2}} $$

    Use equation #rkt‑e2 and parametrize the curve using \(x\) as the parametrization variable. Namely:

    $$ \begin{aligned}x = u, \quad \quad y = y(u) = y(x)\end{aligned} $$
    This yields a very elegant expression, as \( x'(u) = 1 \) and \( x''(u) = 0 \), which lets us arrive at the desired expression #rkt‑e3.

    System comparison: Cartesian/polar/tangent-normal

    Cartesian Polar Tangent-Normal
    Position
    $$ \vec{r} = x\hat\imath + y \hat\jmath $$
    $$ \vec{r} = r \hat{e}_r $$
    $$ s $$
    Velocity
    $$ \vec{v} = \dot{x}\hat\imath + \dot{y} \hat\jmath $$
    $$ \vec{v} = \dot{r} \hat{e}_r + r\dot{\theta}\hat{e}_\theta $$
    $$ \vec{v} = \dot{s}\hat{e}_t $$
    Acceleration
    $$ \vec{a} = \ddot{x}\hat\imath + \ddot{y} \hat\jmath $$
    $$ \vec{a} = (\ddot{r} - r\dot{\theta}^2 ) \hat{e}_r + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \hat{e}_\theta $$
    $$ \vec{a} = \ddot{s}\hat{e}_t + \dot{s}^2 \kappa \hat{e}_n $$

    Applications

    Celestial velocities

    We normally think of our classroom or laboratory as being stationary when we are doing dynamics. But how valid is this assumption?

    We will consider motion due to:

    1. Spinning of the Earth about the North-South axis.
    2. Orbit of the Earth about the Sun.
    3. Rotation of the Sun around center the Milky Way.
    4. Motion of the Milky Way through the universe.

    As we will see below, some of these velocities are not small. Why is normally valid to assume that we are in an inertial reference frame?

    Reference material

    Periods of rotation

    The different types of motion have magnitudes roughly given in the following table. These motions are not all in the same direction, and may add to each other or act in opposite or even orthogonal directions.

    Earth spin Earth orbit Milky Way Through CMB
    period \(T\) \(24\rm\ h\) \(365\rm\ d\) \(200\rm\ My\)
    \(8.64 \times 10^4\rm\ s\) \(3.16 \times 10^7\rm\ s\) \( 6.31 \times 10^{15}\rm\ s \)
    radius \(r\) \(6370\rm\ km\) \(1\rm\ AU\) \(27.2\rm\ kly\)
    \(6.37 \times 10^6\rm\ m\) \( 1.50 \times 10^{11}\rm\ s \) \( 2.57 \times 10^{20}\rm\ s \)
    ang. vel. \(15.0^\circ/\rm h\) \(0.986^\circ/\rm d\) \(1.8^\circ/\rm My\)
    \(\omega = 2\pi/T\) \( 7.27 \times 10^{-5}\rm\ s \) \( 1.99 \times 10^{-7}\rm\ s \) \( 9.97 \times 10^{-16}\rm\ s \)
    velocity \(1670\rm\ km/h\) \(107\,000\rm\ km/h\) \(922\,000\rm\ km/h\) \(1\,990\,000\rm\ km/h\)
    \(v = r\omega\) \(4.63 \times 10^2\rm\ m/s\) \(2.98 \times 10^4\rm\ m/s\) \(2.56 \times 10^5\rm\ m/s\) \(5.52 \times 10^5\rm\ m/s\)
    acceleration \(0.343\%\ g\) \(0.0605\%\ g\) \( 2.60 \times 10^{-9} % g \)
    \(a = r\omega^2\) \( 3.37 \times 10^{-2}\rm\ m/s^2 \) \( 5.93 \times 10^{-3}\rm\ m/s^2 \) \( 2.55 \times 10^{-10}\rm\ m/s^2 \)

    Did you know?

    The first people to have a rough idea of the radius of the Earth and the distance to the Sun were the ancient Greeks. Eratosthenes (276–195 BCE) computed the radius of the Earth to be 40 000 stadia (6800 km) by measuring the difference in Sun angle between Aswan and Alexandria.

    Aristarchus of Samos (310–230 BCE) obtained the first estimates of the distance to the Sun by using observations of lunar eclipses and solar parallax. While his method was in principle correct, poor observational data meant that his computed Earth-Sun distance was quite inaccurate.

    Solar and sidereal time

    We all know that one day is 24 hours long. But the period of the Earth's rotation is not 24 hours! This is because of the difference between solar time and sidereal time. Solar time is the time measured against the Sun, as we normally do. Sidereal time is measured against the stars, which is slightly different.

    Schematic of the Earth's rotation about its own axis and about the sun, counting solar days and sidereal days. Here the Earth has just 8 solar days per year for better visualization.

    As we can see above, the Earth rotates one more sidereal day each year than solar days. This means:

    $$ \text{1 solar year} = \text{365 solar days}= \text{366 sidereal days} $$

    and so:

    $$ \begin{aligned}\text{sidereal day} &= \frac{365}{366}\ \text{solar day} \\&= \frac{365}{366} \times 24\ {\rm h} \\&= 23.93{\rm\ h} \\&= 23{\rm\ h}\ 56{\rm\ min}\end{aligned} $$

    The Earth's orbital angular velocity is thus actually \( \omega = 360^\circ / (23.93{\rm\ h}) = 15.04^\circ/\rm h \).

    The relationship between solar and sidereal days can also be computed by considering just a single day, as shown below.

    Diagram of one solar day and one sidereal day for the Earth, not drawn to scale. The fact that \( \omega_{\rm E} \) and \( \omega_{\rm S} \) are in the same direction means that sidereal days are shorter than solar days (this is not a coincidence).

    Just as for the definition of a day, there is a similar distinction between the synodic lunar month, which is the time between passes of the Moon between the Earth and the Sun, and the sidereal lunar month, which is the orbital period of the Moon in an inertial frame. In common usage, the phrase lunar month refers to the synodic month.

    Did you know?

    Just as sidereal days and solar days are different, the exact length of one year depends on how we define it. The sidereal year is the time for the Earth to complete one orbit relative to the fixed stars, and has length 365.256363 solar days. The tropical year is the time for the Earth to return to the same point in the seasons, which varies around a value of about 365.242189 solar days (about 20 minutes shorter than the sidereal year). These years are different because of the axial precession of the Earth.

    In common usage the word “year” refers to the tropical year, as the seasons have historically been more important for people than the motion of the stars. Observe that:

    $$ 365.242 \approx 365 + \frac{1}{4} - \frac{1}{100} + \frac{1}{400} $$

    This is why leap years in our Gregorian calendar add an extra day every 4 years, unless the year is a whole century, except every 400 years. If our calendar used sidereal years instead of tropical, the fact that 365.256363 is slightly larger than 365.25 would mean that about every 200 years we would need to have a double leap year, when there would be two extra days (February 30?).

    While leap years occur because the year is not an exact integer number of days, a similar problem is caused by the fact that the solar day is not exactly 24 × 60 × 60 seconds. The length of the day actually varies somewhat unpredictably due to tidal friction as well as climactic and geologic events such as glacier formation and mass redistribution in the mantle, both of which change the Earth's moment of inertia. To correct for these variations a leap second is occasionally added, in which the last minute of the day has 61 seconds.

    Track transition curves

    For passengers in a car or train, traveling in a straight line at constant speed is the most comfortable motion, as there is no acceleration. Roads or rail lines with only straight lines are rather limiting, however, so we frequently encounter curves, in the most extreme form in large freeway interchanges such as shown below.

    When designing a freeway interchange, one of the most basic questions just what shape the transition curves between the straight-line roads should have. Other considerations then follow, such as stacking the roads above each other and banking the angle of the roads.

    The difficultly in designing curves in roads arises from the need to have a smooth ride for the passengers in the vehicles as they traverse the curves at high speed. In particular, we do not want to have sudden changes in acceleration for the passengers.

    Aerial view of the High Five multi-level stack interchange between I-635 and US 75 in Dallas, Texas, taken with a camera suspended from a kite line. Image source: Fotopedia image, from the flikr image by Jett Attaway (CC BY 2.0) (full-sized image).

    Reference material

    Circular arcs for transition curves

    To understand the issues with transition curve design, we will consider a simple oval track with two straight segments joined by curves at both ends. The simplest curve shapes are semi-circles (half-circles), as shown below.

    Car driving at constant speed around a track with straight line segments joined to perfect semi-circle ends. The graph at the bottom shows the acceleration magnitude versus time. Note the sudden jump in acceleration magnitude when the car switches from a straight line to the curve.

    If we the car driving around the track with semi-circle ends, then we see that there is zero acceleration on the straight segments, but on the semi-circular transition curves the acceleration is inwards with magnitude \( v^2 / \rho \), where \( \rho \) is the radius of curvature. A passenger would thus feel no acceleration on the straight segments, but then would suddenly feel a large sideways acceleration as the vehicle switches to the semi-circles, which would be very uncomfortable and potentially dangerous.

    For passenger comfort, we do not want rapid changes in acceleration for transition curves. That is, we want a low value for the derivative of acceleration with respect to time. The derivative of acceleration is known as jerk, defined by \( \vec{\jmath} = \dot{\vec{a}} \) (for vectors) or \( j = \dot{a} \) (for scalars). With perfect semi-circular ends we see that the jerk is mathematically infinite at the transition to the curve, although in reality it would just be a very high value as the vehicle would not transition to the semi-circle instantaneously.

    Reference material

    While the terms velocity and acceleration are standard for the 1st and 2nd derivatives of position, the names for higher derivatives are not so well-established. While jerk is often used for the derivative of acceleration (so the 3rd derivative of position), the terms jolt, surge, and lurch are also sometimes encountered for this quantity. The derivative of jerk is sometimes called jounce (so it is the 4th derivative of position). Another suggestion is to refer to the 4th, 5th, and 6th derivatives of position as snap, crackle, and pop, respectively.

    Jerk and snap have many applications in engineering and science. For example, jerk and snap have both been used to measure human movement smoothness and diagnose stroke patients (Rohrer et al., 2002) while minimizing snap is often used as a design principle for quadcopter control schemes (Mellinger and Kumar, 2011).

    Changing accelerations (causing jerk) must result from changing forces, due to Newton's second law. Although the terminology is also somewhat loose in this case, the derivative of force with respect to time is often referred to as yank, and the derivative of yank is called tug (the second derivative of force). Third derivatives and higher of force are very rarely encountered, and do not seem to have any names in common usage.

    References
    • D. Mellinger and V. Kumar, Minimum snap trajectory generation and control for quadrotors, in 2011 IEEE International Conference on Robotics and Automation (ICRA), 2520–2525, 2011. DOI: 10.1109/ICRA.2011.5980409
    • B. Rohrer, S. Fasoli, H. I. Krebs, R. Hughes, B. Volpe, W. R. Frontera, J. Stein, and N. Hogan, Movement Smoothness Changes during Stroke Recovery, The Journal of Neuroscience, 22(18): 8297–8304, 2002. Link.

    Smooth transition curves with Euler spirals

    Unlike the sudden switch shown above from a straight line segment (no curvature) to a curved transition curve, we would prefer to have a more gradual transition. An example of this is shown below with the right-hand transition curves changed to use Euler spiral segments, which start curving gradually and then increase the curvature the further the vehicle moves around the curve, before reversing the process on the second half of the curve. Euler spirals are one of the common types of track transition curves and are special because the curvature varies linearly along the curve.

    Car driving at constant speed around a track with perfect straight line segments joined to Euler-spiral segments on the right-hand curve and a semi-circle on the left-hand curve. The red curve is a perfect semi-circle for comparison. Note the continuous transition in acceleration when the car switches from a straight line to the left-hand curve.

    If we the motion around the track with Euler spiral transitions, then we can see from the acceleration magnitude plot that the acceleration does not suddenly jump as the vehicle moves around the right-hand curve. Instead it steadily increases to a maximum value, before decreasing again to zero. The peak acceleration needed on the Euler spiral transitions is somewhat higher than on the semi-circle transitions, but we have avoided the sudden jerk associated with switching from straight line to circular motion.

    Reference material

    The equation for a spiral with linear curvature variation was first derived by the Swiss mathematician Leonard Euler in 1744, hence the name Euler spiral for this curve. The spiral was then independently rediscovered in the late 1800s by civil engineers who were unaware of Euler's work and who named the resulting spiral the clothoid, which is still a commonly used name in traffic engineering. This spiral also arises in the study of near-field diffraction in optics, as developed by the French engineer Augustin-Jean Fresnel and the French physicist Alfred Cornu, for which reason the spiral is also sometimes called the Cornu spiral.

    Euler spiral equation

    An Euler spiral is a curve for which the acceleration magnitude increases at a constant rate as we travel along the curve at uniform velocity. Another way to say this is that the curvature is a linear function of the distance along the curve. To see that this is the same thing, we write the acceleration in a tangential/normal basis as For

    $$ \vec{a} = \ddot{s} \, \hat{e}_t + \kappa v^2 \, \hat{e}_n. $$
    constant-speed motion with speed \(v\), the distance along the curve satisfies \( \dot{s} = v = \text{constant} \), so \( \ddot{s} = 0 \). The acceleration vector thus only has a normal component, and this has magnitude proportional to the curvature \( \kappa = 1/\rho \), where \( \rho \) is the radius of curvature. To have the acceleration increasing linearly along the curve, we thus want the curvature to be a linear function of distance, so \( \kappa = \alpha s \) for some constant \( \alpha \).

    While specifying that \( \kappa = \alpha s \) is enough to define the shape of the Euler spiral curve, finding the explicit equation for the curve is not so easy. We first introduce the functions \(C(z)\) and \(S(z)\), known as Fresnel integrals and defined by:

    Fresnel integrals #avt-ef
    $$ \begin{aligned}C(z) &= \int_0^z \cos\Big(\frac{1}{2} \pi u^2\Big) du \\S(z) &= \int_0^z \sin\Big(\frac{1}{2} \pi u^2\Big) du\end{aligned} $$

    The Fresnel integrals do not have any simpler forms in terms of elementary functions, as the integrals in them cannot be computed in closed form.

    Now we define the constant \( \ell = \sqrt{\pi/\alpha} \), and then the position at distance \(s\) along an Euler spiral curve is:

    Euler spiral #avt-ee
    $$ \vec{r} = \ell C(s / \ell) \, \hat{\imath}+ \ell S(s / \ell) \, \hat{\jmath} $$

    We start the spiral curve from the origin, initially moving horizontally to the right and curving upwards with constant speed \(v\). Using a tangential/normal basis, let \(\theta\) be the angle of \( \hat{e}_t \) as shown. Then \( \dot{\theta} \) can be found by considering two expressions for the acceleration. First, from the tangential/normal acceleration formula, we have

    $$ \vec{a} = \ddot{s} \, \hat{e}_t + \kappa v^2 \, \hat{e}_n = \alpha s v^2 \, \hat{e}_n, $$
    where we used the fact that \( \ddot{s} = \dot{v} = 0 \) (constant speed) and that \( \kappa = \alpha s \) for some constant \(\alpha\) (the definition of the Euler spiral is that curvature is a linear function of distance \(s\)).

    The second expression for acceleration uses the angular velocity \( \vec{\omega} = \dot\theta \, \hat{k} \) of the tangential/normal basis vectors. Recalling that \( \vec{v} = v \, \hat{e}_t \) and \(v\) is constant, we have

    $$ \begin{aligned} \vec{a} = \dot{\vec{v}} = v \, \dot{\hat{e}}_t = v \, \vec{\omega} \times \vec{e}_t = v \dot{\theta} \, \hat{e}_n. \end{aligned} $$

    Comparing the two expressions for \( \vec{a} \) and using \( s = vt \) we see that

    $$ \dot{\theta} = \alpha s v = \alpha v^2 t $$
    and we can integrate this (with the initial condition that $\(\theta\) starts at zero) to give
    $$ \theta = \frac{1}{2} \alpha v^2 t^2. $$

    To find the equation for \( \vec{r} \) we can integrate the equation

    $$ \dot{\vec{r}} = v \, \hat{e}_t = v \cos\theta \, \hat{\imath} + v \sin\theta \, \hat{\jmath} $$
    starting from \( \vec{r}=0 \) to obtain
    $$ \begin{aligned} \vec{r} &= \int_0^t \left(v \cos\Big(\frac{1}{2} \alpha v^2 \tau^2\Big) \, \hat{\imath} + v \sin\Big(\frac{1}{2} \alpha v^2 \tau^2 \Big) \, \hat{\jmath}\right) d\tau \\ &= \ell \int_0^{s/\ell} \left( \cos\Big(\frac{1}{2} \pi u^2\Big) \, \hat{\imath} + \sin\Big(\frac{1}{2} \pi u^2\Big) \, \hat{\jmath} \right) du, \end{aligned} $$
    where we made the substitution \( \tau = \ell u / v \) with \( \ell = \sqrt{\pi/\alpha} \). Using the definitions of the Fresnel integrals now gives the desired expression.

    Plotting the Euler spiral equation gives the curve below, which starts out at the origin with zero curvature, and the then has steadily increasing curvature as we move along it.

    Euler spiral shape defined by the equation above. Changing the value of \(\alpha\) or \(\ell\) simply scales the whole curve to make it bigger or smaller, without changing the shape.

    The full Euler spiral is unsuitable for track transitions, as the curvature increases without limit. Instead, we can piece together short segments of the Euler spiral to form our transition curve. For example, the right-hand curve in the smooth track above is composed of two copies of the first quarter-turn of the Euler spiral, with one copy flipped upside down. This means the curvature starts at zero, increases linearly to a maximum halfway around the curve, then decreases linearly again back to zero to join the straight segment.