Projectiles with air resistance

Consider a spherical object, such as a baseball, moving through the air. The motion of an object though a fluid is one of the most complex problems in all of science, and it is still not completely understood to this day. One of the reasons this problem is so challenging is that, in general, there are many different forces acting on such objects, including:

gravity
drag
lift
thrust
buoyancy
bulk fluid motion, such as wind
inertial forces, such as the centrifugal and Coriolis forces

In most introductory physics and dynamics courses, gravity is the only force that is accounted for (this is equivalent to assuming that the motion takes place in a vacuum). Here we will consider realistic and accurate models of air resistance that are used to model the motion of projectiles like baseballs.

Wrigley Field in Chicago, Illinois is the home of the Chicago Cubs baseball team. In baseball, an “out of the park” home run is scored when the ball is hit beyond the green outfield (past the yellow foul pole at the left of the above image). Image source: Flickr image by Mike Bash (CC BY NC ND 2.0) (full-sized image).

Reference material

Drag forces and drag coefficients

The drag force is always directly opposed to the velocity of the object. In vector notation, it is defined by the following equation.

$$ \vec{F}_{\rm D} = -F_{\rm D} \hat{v} $$

We consider that $ F_{\rm D} $ is the magnitude of the drag force, and $ \hat{v} $ is the unit vector in the direction of the object's velocity.

Velocity angle from horizontal:

$\theta = \; $ 30$^\circ$

The free body diagram for a baseball subject to gravity and air resistance. Observe that the drag due to air resistance is always in the opposite direction to the velocity. Image credit: Microsoft clip art.

The magnitude of the drag force is characterized by the dimensionless drag coefficient $ C_{\rm D} $, given by the following equation.

$$ C_{\rm D} = \frac{F_{\rm D}}{\frac{1}{2} \rho A v^2} $$

We consider that $ \rho $ is the density of the fluid (in this case, air), $ A=(1/4)\pi D^{2} $ is the cross-sectional area of the object, and $ v $ is the object's speed.

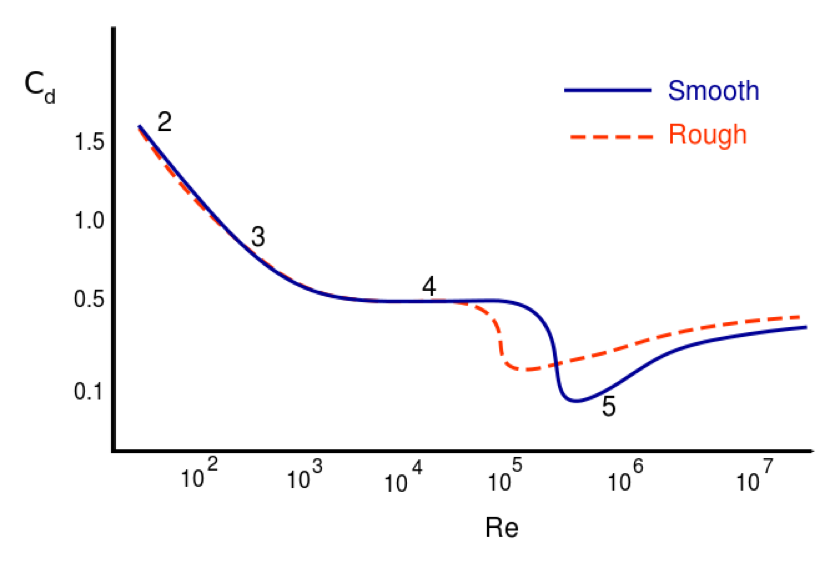
Drag coefficients as a function of Reynolds number

A dimensionless parameter that is very useful in fluid dynamics is the Reynolds number, which is defined by the following equation.

$$ {\rm Re} = \frac{\rho v L}{\mu} $$

We consider that $ L $ is a characteristic length for the flow (in this case, the diameter $ D $ of the ball), and $ \mu $ is the dynamic viscosity of the fluid. The Reynolds number gives a ratio between inertial forces and viscous forces in a fluid flow. For very small Reynolds numbers, the viscous forces are much stronger than the inertial forces (think of trying to stir a cup of honey). For very large Reynolds numbers, the viscous forces are negligible, and we refer to the flow as inviscid (think of stirring a cup of coffee).

An important result in fluid dynamics is that the drag coefficient is a function only of the Reynolds number of the fluid flow about the object. This is defined by the following equation.

$$ C_{\rm D} = C_{\rm D}({\rm Re}) $$

This functional relationship has no closed form. However, the relationship has been established numerically based on experimental data. See Figure #aft-fd for a schematic diagram of the drag coefficient's dependence on the Reynolds number.

Experimental dependence of drag coefficient on Reynolds number for a sphere. Image credit: NASA via Wikipedia.

Quadratic drag model

Notice from Figure #aft-fd that there is a range of Reynolds numbers ($ 10^3 < {\rm Re} < 10^5 $), characteristic of macroscopic projectiles, for which the drag coefficient is approximately constant at about 1/2 (see the part of the curve labeled “4” in Figure #aft-fd). That the drag coefficient is constant means that, within this region, the magnitude of the drag force is proportional to the square of the object’s speed. Substituting $ C_{\rm D}=1/2 $ into the definition of $ C_{D} $ above, we obtain the following equation.

$$ F_{\rm D} = \frac{1}{4} \rho A v^2 = c v^2 $$

We have defined the quadratic drag parameter $c$ with the following equation.

$$ c = \frac{1}{4} \rho A = \frac{\pi}{16} \rho D^2 $$

We consider this is a constant for a given projectile. This is referred to as quadratic drag, because the drag force magnitude is proportional to the square of the speed. Using this result, we can write the drag force vector with the following equation.

$$ \vec{F}_{\rm D} = - c v^2 \hat{v} $$

In the presence of gravity and quadratic drag alone, the net force on an object is given by the following equation.

$$ \sum \vec{F} = m \vec{g} - c v^2 \hat{v} $$

We consider that $ m $ is the mass of the object and $ \vec{g} $ is the local acceleration due to gravity. Below is an interactive graphic showing the trajectory of an object with gravity and quadratic drag. You can change the various parameters to see their effects on the object’s motion.

Initial speed:

$v_0 = \;$ 30 m/s

Initial angle:

$\theta_0 = \;$ 45°

Mass:

$m = \;$ 135 g

Diameter:

$D = \;$ 7.5 cm

Trajectories of a projectile in a vacuum (blue) and subject to quadratic drag from air resistance (red). The air density is $ \rho = 1.225 \rm \ kg / m ^ 3 $ (standard sea-level atmosphere) and the acceleration due to gravity is $ g = 9.81 \rm \ m / s ^ 2 $. A regulation baseball has a mass of about $ m = 145 \rm \ g $ and a diameter of about $ D = 7.5 \rm \ cm $.

Did you know?

There is no well-measured record for longest baseball home run. It is claimed that Mickey Mantle hit a ball 643 feet (196 m), although this apparently included rolling on the ground. Other power hits by Mantle are reliably measured to be over 500 feet (152 m).