Capsizing ships

Background

The MV Golden Ray, a 656-foot long roll-on/roll-off vehicle carrier, collapsed on 8 September 2019 in between the Colonel's Island Terminal in the Port of Brunswick, Georgia, and Baltimore, Maryland.

The MV Golden Ray capsized on 8 September 2019 in St. Simons Sound near the Port of Brunswick in Georgia, United States. Image credit: U.S. Coast Guard District 7 PADE (CC PDM 1.0).

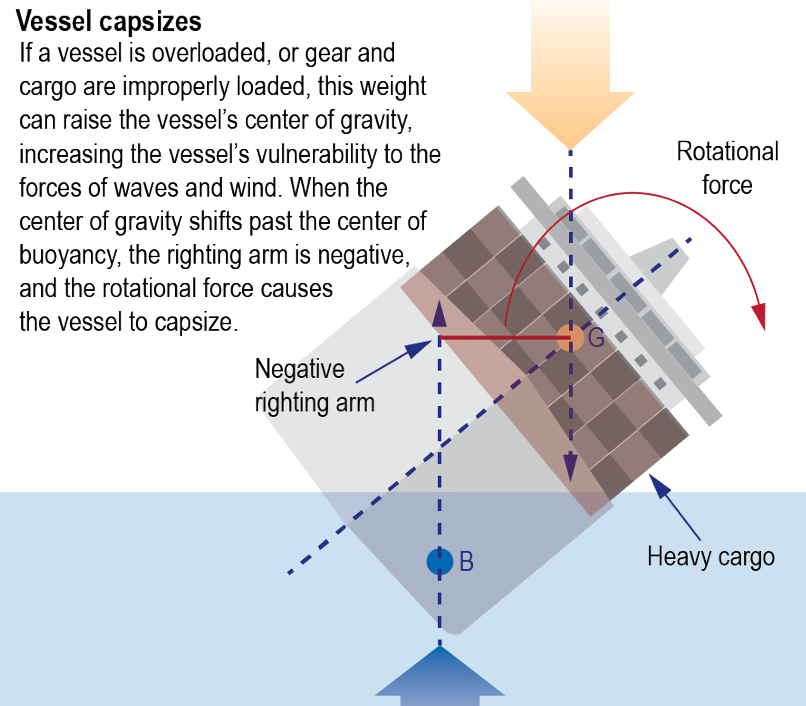
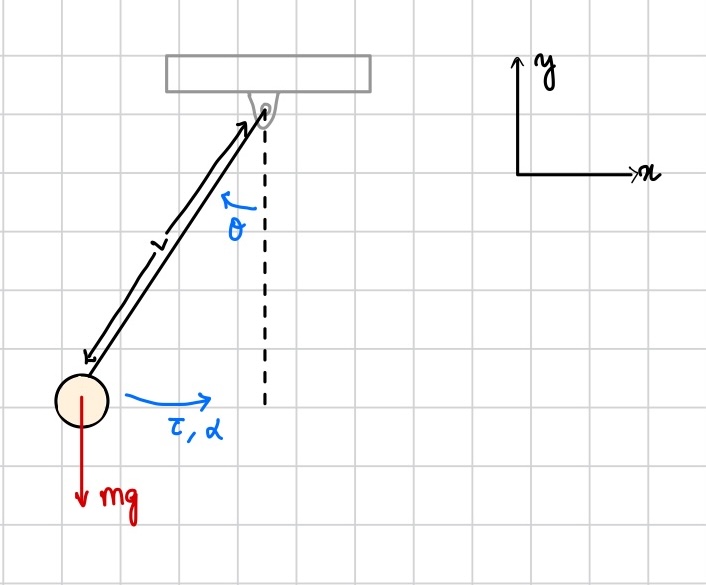
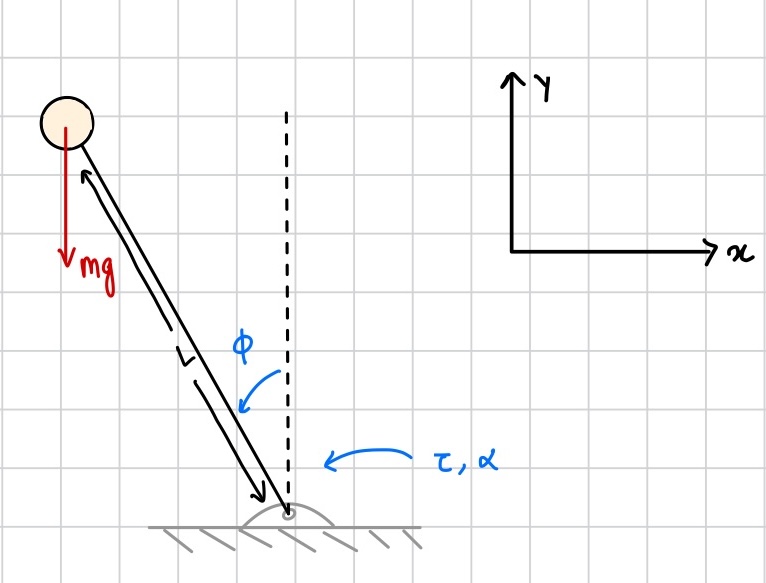
After an investigation by the National Transportation Safety Board (NTSB), it was found that the ship collapsed due to the use of erroneous ballast (cargo, weights, etc.) quantities in the stability calculation program, which produced incorrect stability conditions of the ship. In other words, a moment was generated from the location difference between the center of mass and the center of buoyancy. This moment arm produced an angular acceleration ($ \alpha $) opposite to the angular displacement ($ \theta $), meaning the ship was unstable. This failure to account for changes in ballast quantities meant the ships hull could not provide a counter moment to these forces, and the ship capsized.

Reference material.

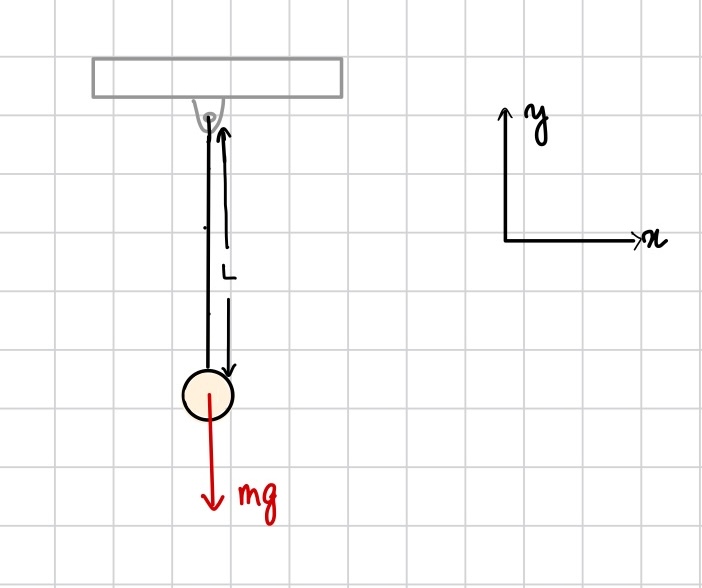
This application uses center of mass.

Extra!

Supplemental video:

Watch how boats can be engineered and tested to correct any capsizing movements.

Review?

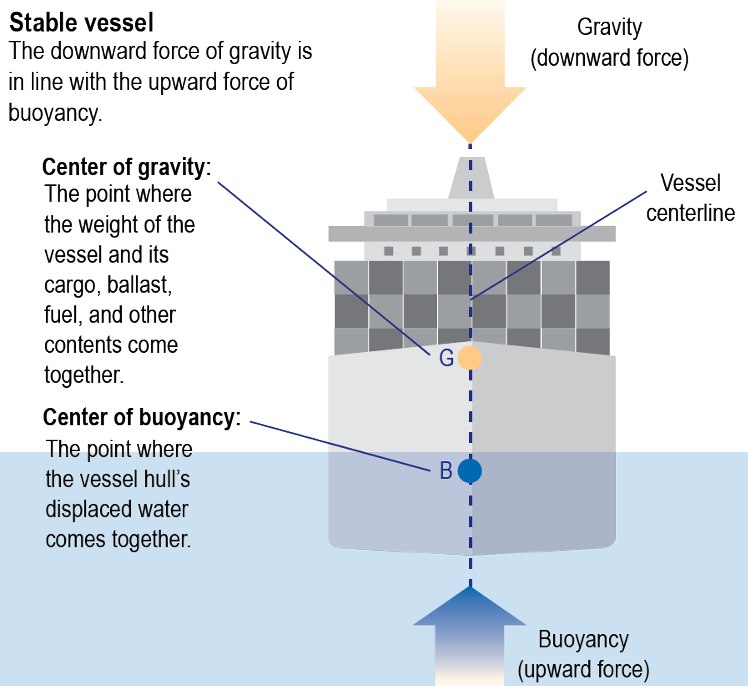
The center of buoyancy ($ B $) is the point where the total buoyant force on a submerged or floating object acts. You can think of it as the center of gravity of the volume of fluid displaced by the object. This term is crucial for understanding stability and equilibrium in hydrodynamics.

Principles of stability

< >

Image credit: National Transportation Safety Board

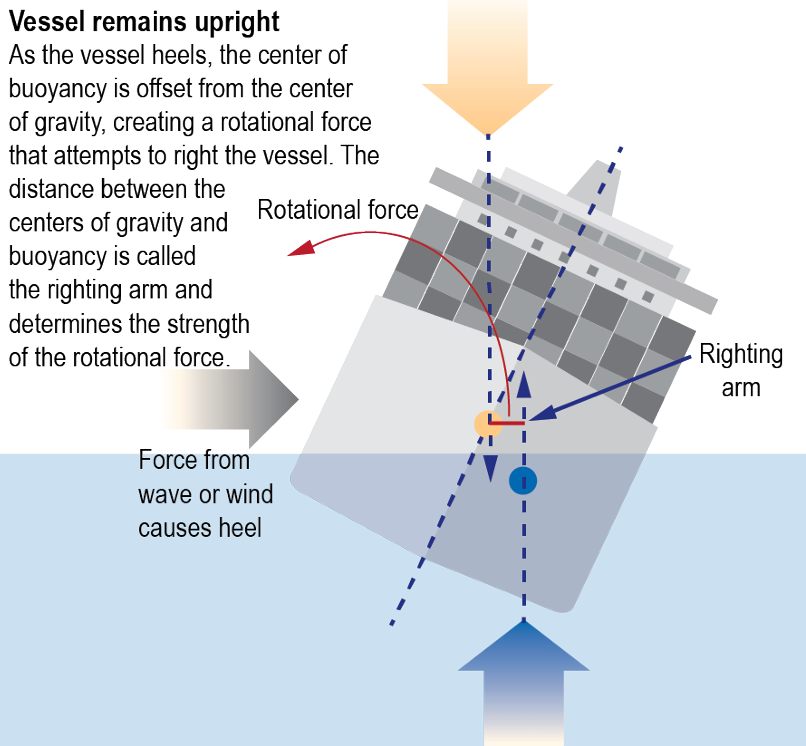
Ship stability reflects the relationship between buoyancy (the force pushing up on the ships center of buoyancy, $ B $) and gravity (the force pushing down on the ships center of gravity, $ G $). When a vessel is floating upright, the force of gravity and buoyancy are vertically aligned. Vessel stability is usually expressed as the heeling (tilting) moment magnitude necessary to capsize the ship at a specified heeling angle.

When a disturbing force, such as waves or wind, exerts an inclining moment on a ship, the ship's underwater volume shifts, causing the center of buoyancy to move. A ship's metacenter ($ M $) is the virtual intersection between the lines from (1) the original center of buoyancy and (2) the new, heeling center of buoyancy. The distance from a ship's center of gravity to its metacenter is known as the metacentric height ($ GM $), and is used to determine stability. A negative value indicates instability.

Unless the ballast is allowed to change, the center of gravity remains the same, causing the two force directions to become unalligned, risking this negative $ GM $ value. If ballast allows the restoring moment exertion to bring the ship to an even keel, the $ GM $ is positive and the moment is known as the righting moment arm.

Stability comparisons

Simple pendulum

A simple pendulum can be thought of as a mechanical analog of a ship. Simple pendulums experience a restoring torque when in an unstable position that brings it back to equilibrium, similar to the function of a righting moment in the example above. This corresponds to a ship having a low center of gravity.

< >

Characteristic equation of a pendulum. #eqn-pend

$$ \begin{aligned} \ddot \theta = - \frac{g}{l} \sin(\theta) \end{aligned} $$

For a simple pendulum, the rest, or vertical, position where the angular displacement at ($ \theta=0 $) is the position of marginally stable equilibrium. Equilibrium is only marginally stable because an oscillatory system, like a simple pendulum, has a limited output range but does not achieve steady state after an excitation. At $ \theta=0 $, its potential energy is lowest while the kinetic energy is maximized. However, at the two extrema on either side of the rest position, the $ \theta $ is maximum and the pendulum has the maximum potential energy. This configuration induces a restoring torque ($ \tau $) that produces an $ \alpha $, which is opposite to the direction of the angular displacement. The implication is that these extrema are unstable for the simple pendulum.

Inverted pendulum

However, in the case of an inverted pendulum, there is no stable equilibrium position. This corresponds to a ship having a high center of gravity.

< >

For an inverted pendulum, the rest position with $ \phi=0 $ is unstable since its potential energy is maximized. This is an unstable system since the output due to an excitation is unbounded, unlike a simple pendulum. When the pendulum is displaced by a value of $ \phi $, the torque induced is in the direction of the angular displacement (i.e., $ \alpha $ and $ \phi $ have the same signs). In the case of a ship, the high center of gravity means there is a high risk of capsizing.