Geometric properties
Center of mass (COM)
The total mass of a rigid body is as follows:
The mass of an infinitesimally small element of the rigid body \(dm\) assuming constant density is: \[ dm = \rho \, dV \] Therefore, integrating over the entire volume of the body gives us the expression above.
The center of mass of a rigid body can be calculated as follows:
\( \vec{r} \) is the vector from a reference origin \( O \) to \( dV \).
The integral term \( \iiint_{\mathcal{B}} \rho \vec{r} \, dV \) is known as the "first moment of mass".
The center of mass of a collection of particles is given by the finite sum:
Therefore, for a continuous mass distribution and infinite number of particles, the sum becomes an integral and the masses become the mass of an infinitesimally small element on the rigid body:
Where \( dm = \rho \, dV \) from the differential of #rcm-tm. Substituting in:
A solid uniform right-triangular plate with mass \( m \) has width \( w \), height \( h \). Where is the center of mass \( \vec{r}_C \)located?
In order to figure out where the center of mass is located, we will need to choose an origin. The origin chosen in this instant is where the base and height begin, as shown. Using the center of mass formula will allow us to calculate the vector shown below (i.e we are calculating \( \vec{r}_{OC} \)).
Using the formula #rcm-cm:
Where \( A \) represents the surface area of the plate, and \( t \) is the thickness. We will assume the thickness is 1, as we are only interested in the center of mass in the \( x \)-\( y \) plane. Our triple integral with \( dV \)instead becomes a double integral with \( dV = t dA \). We therefore have:
We will redraw the figure and show the \(dA\) element. We will also find the \(x\)-coordinate and \(y\)-coordinate ranges for the body.
Examining the figure above, we can see that the \( x \)-coordinate range is \( 0 \) to \( w \). Our \( y \)-coordinate range has a dependence on the \( x \)-value, and the equation of the hypotenuse is \( y = h - \frac{h}{w}x \), using the point-slope formula. Therefore, the \( y \)-coordinate range is \( 0 \) to \( h - \frac{h}{w}x \). As a result of this, we will have to integrate with respect to \( y \) first. All in all, our center of mass equation becomes:
where \( vec{r} \) is the distance to the \( dA \) element. We can see the coordinates of \( dA \) are \([x,y]\). Thus, \( \vec{r} = x\hat{\imath} + y\hat{\jmath} \). Therefore:
where \( \frac{\rho}{m} = \frac{1}{A} = \frac{1}{\frac{1}{2}wh} = \frac{2}{wh} \). Substituting that in yields:
Meaning the center of mass for a right-triangular plate is located at 1/3rd of the width, and 1/3rd of the height. This formula has been used to calculate the center of mass of different common shapes.
Finding the center of mass allows us to treat complex shapes as point-masses with all their mass at the center of mass.
To find the center of mass of a body made up of composite shapes, we simply do the weighted average of each body by using the fact above.
\( \vec{r}_i \) is the center of mass of the \(i\)th body. The whole body \( \mathcal{B} \) is composed of sub-bodies \( \mathcal{B}_1 \) and \( \mathcal{B}_2 \)
Finding the center of mass of the whole body follows directly from the fact that the integral over the whole body is the sum of the integrals over the sub-bodies. That is, for \( \mathcal{B} = \mathcal{B}_1 \cup \mathcal{B}_2 \) (and \( \mathcal{B}_1 \)not overlapping with \( \mathcal{B}_2 \), we have:
A solid uniform L-shaped plate has mass \(m\) and dimensions as shown. What is the location of the center of mass?
In order to figure out where the center of mass is located, we will need to choose an origin. The origin chosen here is the corner shown.
Then we must realize that the L-shape can be decomposed into four square plates, as shown. Each square plate has the same mass, so:
Using the addition formula #rcm-cb:
where:
Substituting in:
Thus, the center of mass of the L-shape plate:
And its location on the plate is shown below.
Recap
| Type of shape | Operation |
|---|---|
| Simple shapes | Symmetry tables |
| Combination of simple shapes | Find each c.o.m and then combine |
| Complex shapes | Integrate |
Basic shapes
The centers of mass listed below are all computed directly from the integral #rcm-cm. Note the center of mass provided is the vector from point \(O\) (the reference origin).
The total mass of the plate is \( m = \rho A = \rho \ell_x \ell_y \). Thus we have:
It is convenient to do a linear transformation from \(x\)-\(y\) plane to the \(u\)-\(v\) plane, to transform the triangle into a right-triangle with \(b = 1\), \(h = 1\):
Or solve the following system of equations:
We find that the linear transformation is:
The Jacobian of this coordinate transformation is:
Starting with the \(x\)-coordinate:
The total mass of the plate is \( m = ho A = rac{1}{2} ho x_P y_Q \), and with the chosen configuration \(y_P = 0\). Thus:
It is convenient to switch to cylindrical coordinates:
The Jacobian of this coordinate transformation is:
Therefore:
The total mass of the sector is \( m = \rho A = \frac{\theta}{2}\rho ab \). Thus:
Simplified shapes
The centers of mass listed below are all special cases of the basic shapes given in Section #rcm-bs. Other special cases can be easily obtained by similar methods, or directly computing the integral.
See example problem on how to derive it by directly computing the integrals.
The other perhaps simpler approach is to let \(x_Q = 0\) in #rcm-et, which forms a right triangle if the configuration is the same as the one shown in the figure. Thus:
See example problem on how to derive it by directly computing the integrals.
The other perhaps simpler approach is to let \(x_Q = 0\) in #rcm-et, which forms a right triangle if the configuration is the same as the one shown in the figure. Thus:
We could use the integral definition of the center of mass and compute it directly:
It is convenient to switch to cylindrical coordinates:
The Jacobian of this coordinate transformation is:
Therefore:
The total mass of the sector is \( m = \rho A = \frac{\theta}{2}\rho r^2 \). Thus:
Another way to reach this formula is to use #rcm-ee, and for a circular sector, let \(a = b = r\).
Using #rcm-ec, for a semi-circular sector, the angle \( \theta = \pi \). Therefore:
Moment of inertia
The moment of inertia of a body, written \( I_{P,\hat{a}} \), is measured about a rotation axis through point \(P\) in direction \( \hat{a} \). The moment of inertia expresses how hard it is to produce an angular acceleration of the body about this axis. That is, a body with high moment of inertia resists angular acceleration, so if it is not rotating then it is hard to start a rotation, while if it is already rotating then it is hard to stop.
The moment of inertia plays the same role for rotational motion as the mass does for translational motion (a high-mass body resists is hard to start moving and hard to stop again).
The distance \(r \) is the perpendicular distance to \( dV \) from the axis through \(P\) in direction \( \hat{a}. \)
Be advised that the "moment of inertia" encountered in Statics is not the same as the moment of inertia used in Dynamics. Strictly speaking, the "moment of inertia" from Statics shouldn't even be called "moment of inertia." What it really is is the "second moment of area." Below are the definitions of two such second moments of area:
In contrast, the moment of inertia (about the \(z\)-axis) is defined as stated above.
For example, a rectangle of base \(b\) and height \(h\) has the following moments about its centroid \(C\):
Notice that the dimensions of the two quantities are different. While the dimension of second moment of area is \( (\text{length})^{4} \), the dimension of moment of inertia is \( (\text{mass})(\text{length})^{2} \). When doing dynamics problems with moments of inertia, you should not use the formulas you remember for second moment of area instead. You will get the wrong answer!
Observe that the moment of inertia is proportional to the mass, so that doubling the mass of an object will also double its moment of inertia. In addition, the moment of inertia is proportional to the square of the size of the object, so that doubling every dimension of an object (height, width, etc) will cause it to have four times the moment of inertia.
The coordinates \((x,y,z)\) in the body are measured from point \(P\).
The distance\(r\) in the moment of inertia integral #rem-ei is the perpendicular distance from the axis of rotation to the infinitesimal volume \(dV \). If we are using rectangular coordinates \((x,y,z)\) measured from point \(P\), and the axis of rotation is one of the coordinate axes, then the perpendicular distance is very simple.
As an example, consider the case when the axis of rotation \( \hat{a} \) is the \( \hat{k} \) axis, as shown in the figure. Then the perpendicular distance \(r\) satisfies \(r^2 = x^2 + y^2\), giving the coordinate expression above. The other two coordinate axes are similar.
A solid square uniform plate has mass \(m\), side-length \( \ell \), and thickness \( h \). What is the moment of inertia about the \(z \)-axis through the center of mass \(C\)?
We will use the coordinate formula #rem-ec. To do this, we measure the position from the point \(C\) about which we are computing the moment of inertia, so the coordinate origin is at \(C\). The figure to the right shows the 3D configuration of the body, where we see that the \(x\)-coordinate range of the body is \(-\ell/2\) to \(\ell/2\), and the same for the \(y\)-coordinate, while the \(z\)-coordinate ranges from \(-h/2\) to \(h/2\).
Taking the density of the plate to be \(\rho\), we thus have:
Did you know?
We are always considering the moment of inertia to be a scalar value \( I \), which is valid for rotation about a fixed axis. For more complicated dynamics with tumbling motion about multiple axes simultaneously, it is necessary to consider the full 3 × 3 moment of inertia matrix:
The three scalar moments of inertia from #rem-ec appear on the diagonal. The off-diagonal terms are called the products of inertia and are given by
and similarly for the other terms. The angular momentum of a rigid body is given by \( \vec{H} = I \vec{\omega} \), which is the matrix product of the moment of inertia matrix with the angular velocity vector. This is important in advanced dynamics applications such as unbalanced rotating shafts and the precession of gyroscopes.
Parallel axis theorem
Here \( d \) is the perpendicular distance between the axes through \( P \) and \(C \) in direction \( \hat{a} \), so \( d = \| \operatorname*{Comp}(\vec{r}_{CP}, \hat{a})\| \).
To easily compute the moments of inertia relative to axes through \( P \) and \( C \) it is easiest to choose a coordinate system aligned with the rotation axis direction \( \hat{a} \). We will choose coordinates \( (x,y,z) \) measured from the center of mass \( C \) and with the \(z\)-axis \( \hat{k} \) in the direction of \( \hat{a} \), as shown in the figure.
As we integrate over the body with infinitesimal volume \( dV \) at position \( (x,y,z) \) from \( C \), we will write the distance from the axis through \( C \) as \( r_c \) and the distance from the axis through \( P \) as \( r_P \), as illustrated. The distance between the two rotation axes is \( d \). In the chosen coordinate system this means that:
where \( P \) has position \( (x_P, y_P, z_P) \) in these coordinates.
Computing the integral #rem-ec to find the moment of inertia about the axis through \( P \) in direction \( \hat{a} \) now gives:
The parallel axis theorem does not apply to any two parallel rotation axes. The rotation axis on the right-hand-side of the equation must be through the center of mass \( C \), although the other axis can be through any point \( P \).
The distance \( d \) in the parallel axis theorem is the perpendicular distance between the axes through points \( P \) and \( C \). This will normally not be the same as the distance \( r_{CP} \) between \( P \) and \( C \), except in 2D problems or if it happens that \( \vec{r}_{CP} \) is already perpendicular to the rotation axis \( \hat{a} \). The distance \( d \) can be computed by taking the orthogonal complement of \( \vec{r}_{CP} \) with respect to \( \hat{a} \), so \( d = \|\operatorname{Comp}(\vec{r}_{CP}, \hat{a})\| \).
In Example Problem #rem-xs we computed the moment of inertia of a square place about the center to be \( I_{C,z} = \frac{1}{6} m \ell^2 \). The parallel axis theorem #rem-el now gives:
To check our answer, we can compute the corner moment of inertia directly by integrating with formula #rem-ec. To do this, we put the coordinate origin at the point \( P \) about which we wish to find the moment of inertia, as shown in 3D to the right. From this we see that the \(x \)range is \(0\) to \( \ell \), the same for the \( y \) range, and the \(z\) range is \(-h/2\) to \(h/2\).
The integral formula now gives:
One consequence of the parallel axis theorem is that the moment of inertia can only increase as we move the rotation point \( P \) away from the center of mass \( C \). This means that the point with the lowest moment of inertia is always the center of mass itself.
A second consequence of the parallel axis theorem is that moving the point \( P \) along the direction \( \hat{a} \) doesn't change the moment of inertia, because the axis of rotation is not changing as the point moves along the axis itself.
Additive theorem
The whole body \( \mathcal{B} \) is composed of sub-bodies \( \mathcal{B}_1 \) and \( \mathcal{B}_2 \).
The addition of moments of inertia for sub-bodies to give the full moment of inertia follows directly from the fact that the integral over the whole body is the sum of the integrals over the sub-bodes. That is, for \( \mathcal{B} = \mathcal{B}_1 \cup \mathcal{B}_2 \) (and \( \mathcal{B}_1 \) not overlapping with \( \mathcal{B}_2 \)), we have:
It is only valid to add together moments of inertia for different sub-bodies if each moment of inertia is computed about the same axis of rotation. For example, consider \( I^{\mathcal{B}_1}_{C_1,z} \) and \( I^{\mathcal{B}_2}_{C_2,z} \), which are the moments of inertia of bodies \( \mathcal{B}_1 \) and \( \mathcal{B}_2 \) about each of their individual centers of mass \( C_1 \) and \( C_2 \) (with axis direction \( z \)). Now it is physically meaningless to form the sum \( I^{\mathcal{B}_1}_{C_1,z} + I^{\mathcal{B}_2}_{C_2,z} \), because each moment of inertia is about a different axis. We must first shift both moments of inertia to a common axis point \( P \) (perhaps by using the parallel axis theorem), and then we can meaningfully add them together.
A solid uniform L-shaped plate has mass \(m\) and dimensions as shown. What is the moment of inertia about the \(z\)-axis through the corner \(P\)?
Recall that in Example Problem #rem-xs we computed the moment of inertia of a square place about the center to be \( I_{C,z} = \frac{1}{6} m \ell^2 \).
To use this together with the parallel axis theorem #rem-el and the additive theorem #rem-ea, we must first realize that the L-shape can be decomposed into four square plates, as shown. Each small square body has the same mass and the same moment of inertia about its center, so:
Now individual moments of inertia about the corner \(P\) can be found using the parallel axis theorem:
Combining the individual moments of inertia now gives us the total:
Basic shapes
The moments of inertia listed below are all computed directly from the integrals #rem-ec.
The calculation for any of the axes is the same, so we will only write out the derivation of \( I_{C,z} \) here. We use #rem-ec, which gives:
The total mass of the plate is \( m=\rho\ell_x\ell_y\ell_z \), so we can write the moment of inertia as
To compute the integrals in #rem-ec it is convenient to switch to cylindrical coordinates:
The Jacobian of this coordinate transformation is:
Starting with the \( z \) axis, the moment of inertia is thus:
To compute the integrals in #rem-ec it is convenient to switch to spherical coordinates:
Simplified shapes
The moments of inertia listed below are all special cases of the basic shapes given in Section #rem-sb. Other special cases can be easily obtained by similar methods.
A rod is assumed to be a shape with infinitesimally small cross-section. We can use the formula #rem-ey for a cylinder with zero radii \( r_1 = r_2 = 0 \) . The coordinates here are set up so that \( z \) is orthogonal to the rod axis and \( x \) is along the axis, so #rem-ey gives:
To find the moment of inertia about the end point \( P \) we can use the parallel axis theorem #rem-el. This results is:
The moment of inertia \( I_{P,x} \) is still zero, because \( \vec{r}_{CP} \) is parallel to \( x \).
The solid cylinder expressions are simply the cylindrical thick shell formulas #rem-ey with the inner radius set to \( r_1 = 0 \) and the outer radius \( r_2 = r \) .
The hollow cylinder expressions can be found from cylindrical thick shell formulas #rem-ey by taking the same value for both inner and outer radii, so that \( r_1 = r_2 = r \) .
All axes through \( C \) have the same moment of inertia.
The solid ball moment of inertia can be directly obtained from the spherical thick shell expression #rem-es with inner radius \( r_1 = 0 \) and outer radius \( r_2 = r \) .
All axes through \( C \) have the same moment of inertia.
Instead we need to set \( r_2 = r \) and then to take the limit as \( r_1 \to r \) using l'Hôpital's rule:
Instantaneous center (M)
- For a rigid body moving in 2D (rotating and possibly translating)
- Instantaneous center “M” is the point on or off the rigid body that has zero velocity at that instant (i.e. no translation at this point)
- Point that the body rotates about (at that instant in time)
Graphical rules for finding M
(Assuming that figure is drawn to scale, including velocity vectors)
- Draw lines perpendicular to velocities
- If the lines intersect at a single point, that point is M
- If the lines are colinear:
- Draw 2 lines that connect the tips of velocity vectors
- If the lines intersect at a single point, that point is M
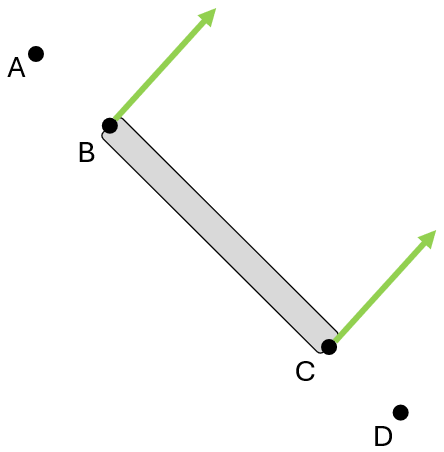
Find the instantaneous center (M) and the direction of \( \vec{v}_B \) of the beam.
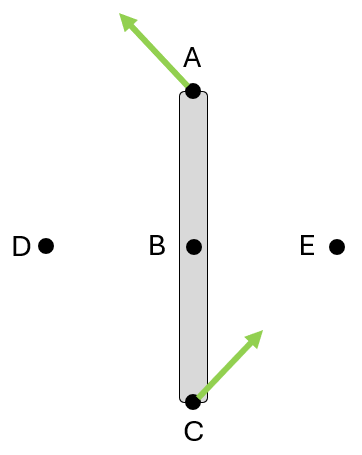
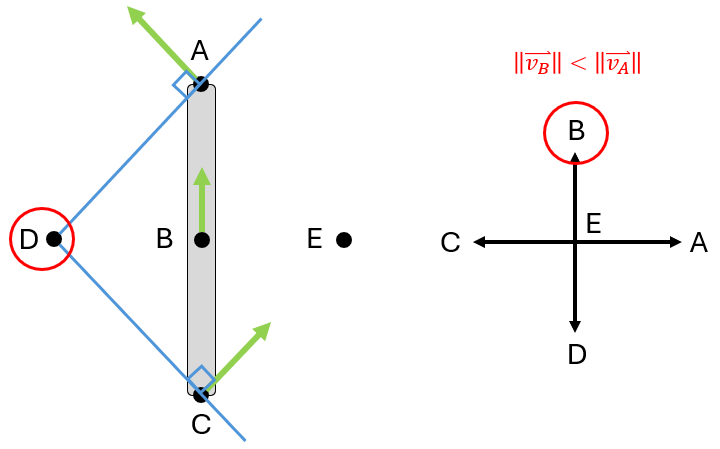
Find the instantaneous center (M) and the direction of \( \vec{v}_B \) of the beam.
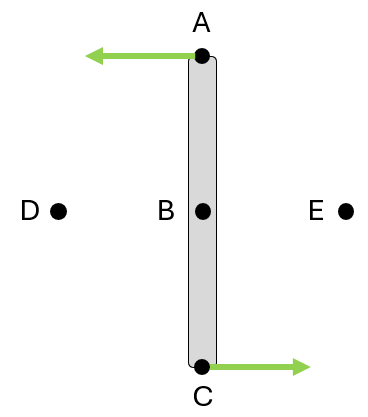
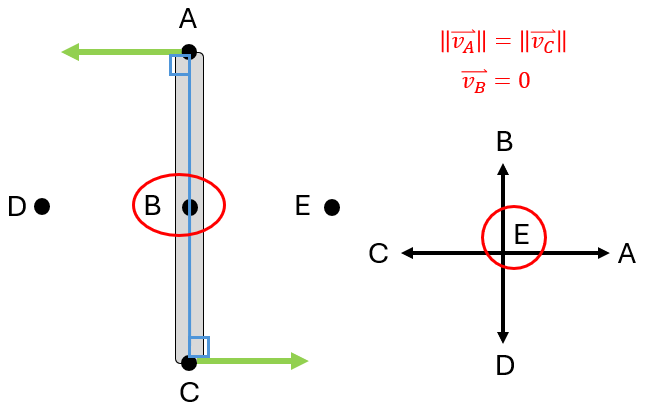
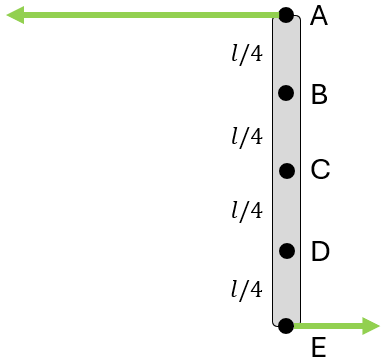
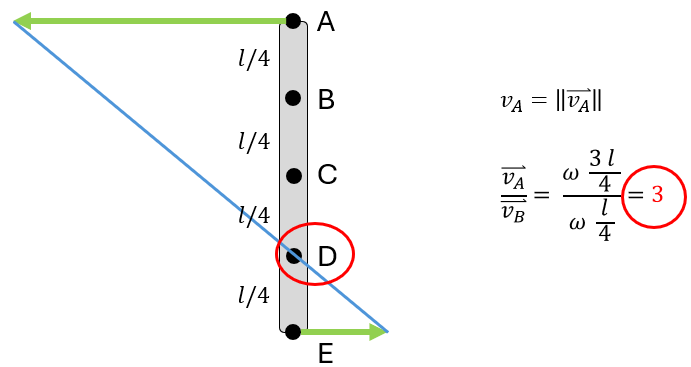
Find the instantaneous center (M) and the direction of \( v_A / v_B \) of the beam.
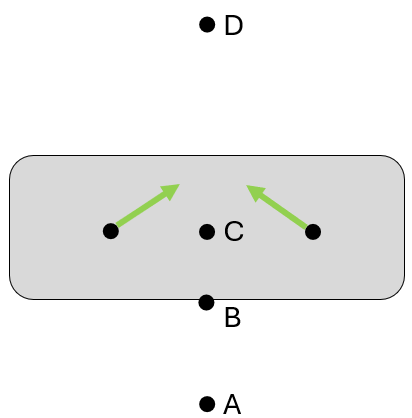
Find the instantaneous center (M).
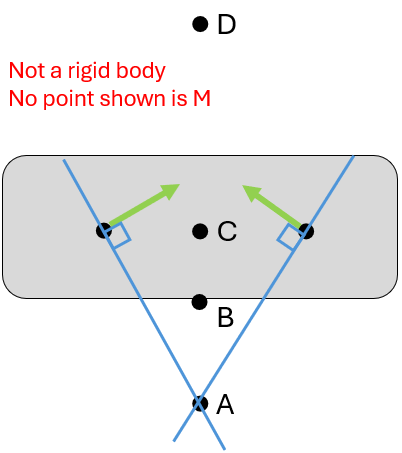
Find the instantaneous center (M).
The body is not rotating
- Consistent direction of rotation.
- Consistent speeds \( v = \omega \, r \).
- Body may not be rotating (pure translation).