Vectors and scalars
Vectors
A vector is an arrow with a length and a direction. Just like positions, vectors exist before we measure or describe them. Unlike positions, vectors can mean many different things, such as position vectors, velocities, etc. Vectors are not anchored to particular positions in space, so we can slide a vector around and locate it at any position.
Change:
Two vectors, which may or may not be the same vector. Moving a vector around does not change it: it is still the same vector.
Notation
Some textbooks differentiate between free vectors, which are free to slide around, and bound vectors, which are anchored in space. We will only use free vectors.
We will use the over-arrow notation \( \vec{a} \) for vector quantities. Other common notations include bold \( \boldsymbol{a} \) and under-bars \( \underline{a} \). For unit (length one) vectors we will use an over-hat \( \hat{a} \).
Scalars
While a vector represents magnitude and direction, a scalar is a number that represents a magnitude, but with no directional information. Some examples of scalar quantities can be mass, length, time, speed, or temperature.
Vector addition and subtraction
Vectors can be added or subtracted together, using the parallelogram law of addition or the head-to-tail rule.
Unit vectors
A unit vector is any vector with a length of one. We use the special over-hat notation \( \hat{a} \) to indicate when a vector is a unit vector. Any non-zero vector \( \vec{a} \) gives a unit vector \( \hat{a} \) that specifies the direction of \( \vec{a} \).
Any vector can be written as the product of its length and direction:
Three vectors and their decompositions into lengths and directional unit vectors.
Vector magnitude and direction
Vectors can be written as a magnitude (length) multiplied by the unit vector in the same direction as the original vector.
The length of a vector \( \vec{a} \) is written either \( \| \vec{a} \| \) or just plain \(a\). The length can be computed using Pythagorus’ theorem:
Computing the length of a vector using Pythagorus' theorem.
Some common integer vector lengths are \( \vec{a} = 4\hat\imath + 3\hat\jmath \) (length \(a = 5\)) and \( \vec{b} = 12\hat\imath + 5\hat\jmath \) (length \(b = 13\)).
The direction of a vector can be written as a unit vector by dividing the vector components by the vector magnitude.
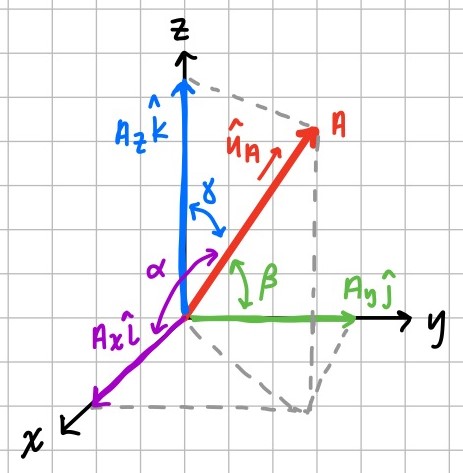
Directional cosines
Alternatively, the vector components can be determined geometrically via the angles of each component with respect to the Cartesian Axes.
Dot product
The dot product (also called the inner product or scalar product) is defined by
An alternative expression for the dot product can be given in terms of the lengths of the vectors and the angle between them:
The fact that we can write the dot product in terms of components as well as in terms of lengths and angle is very helpful for calculating the length and angles of vectors from the component representations.
If two vectors have zero dot product \( \vec{a} \cdot \vec{b} = 0 \) then they have an angle of \( \theta = 90^\circ = \frac{\pi}{2}\rm\ rad \) between them and we say that the vectors are perpendicular, orthogonal, or normal to each other.
Dot product identities
Cross product
The cross product can be defined in terms of components by:
It is sometimes more convenient to work with cross products of individual basis vectors, which are related as follows.
Rather than using components, the cross product can be defined by specifying the length and direction of the resulting vector. The direction of \( \vec{a} \times \vec{b} \) is orthogonal to both \( \vec{a} \) and \( \vec{b} \), with the direction given by the right-hand rule. The magnitude of the cross product is given by:
This second form of the cross product definition can also be related to the area of a parallelogram.
The area of a parallelogram is the length of the base multiplied by the perpendicular height, which is also the magnitude of the cross product of the side vectors.
A useful special case of the cross product occurs when vector \( \vec{a} \) is in the 2D \( \hat\imath,\hat\jmath \) plane and the other vector is in the orthogonal \( \hat{k} \) direction. In this case the cross product rotates \( \vec{a} \) by \( 90^\circ \) counterclockwise to give the perpendicular vector \( \vec{a}^\perp \), as follows.
Cross product identities
Calculating the cross product
The cross products of 3D vectors can be calculated by taking the determinant of specific components of the two vectors. It's best to start by writing a 3x3 matrix with the \( \hat{\imath} \), \( \hat{\jmath} \), and \( \hat{k} \) vectors in the first row and the two vectors you are taking the cross product of in the next two rows. See the example below of the cross product between \( \vec{A} \) and \( \vec{B} \):
Vector projection
The projection and complementary projection are:
Adding the projection and the complementary projection of a vector just give the same vector again, as we can see on the figure below.
Projection of \( \vec{a} \) onto \( \vec{b} \) and the complementary projection.
As we see in the diagram above, the complementary projection is orthogonal to the reference vector: