Shear force & bending moment diagrams
Internal forces of a member can be determined by creating an imaginary cut in a member, and then solving for the internal shear force, normal force, and bending moment (which, after the cut, become "external" forces that can be solved for).
To determine how the internal shear force and bending moment change throughout the member, shear force and bending moment diagrams are created. Shear force diagrams provide a graphical representation of the internal shear force within a member, and bending moment diagrams provide a graphical representation of the internal bending moment within a member.
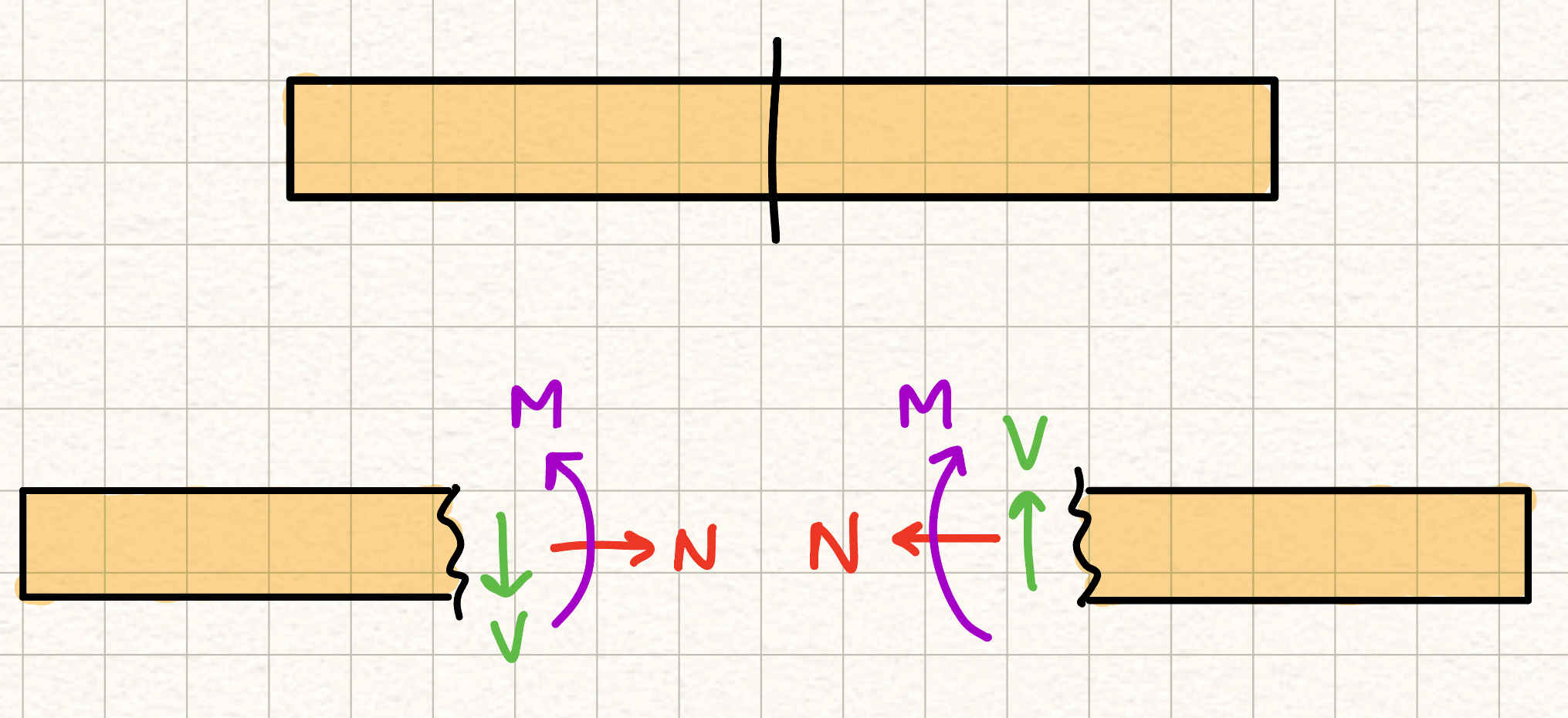
Sign conventions
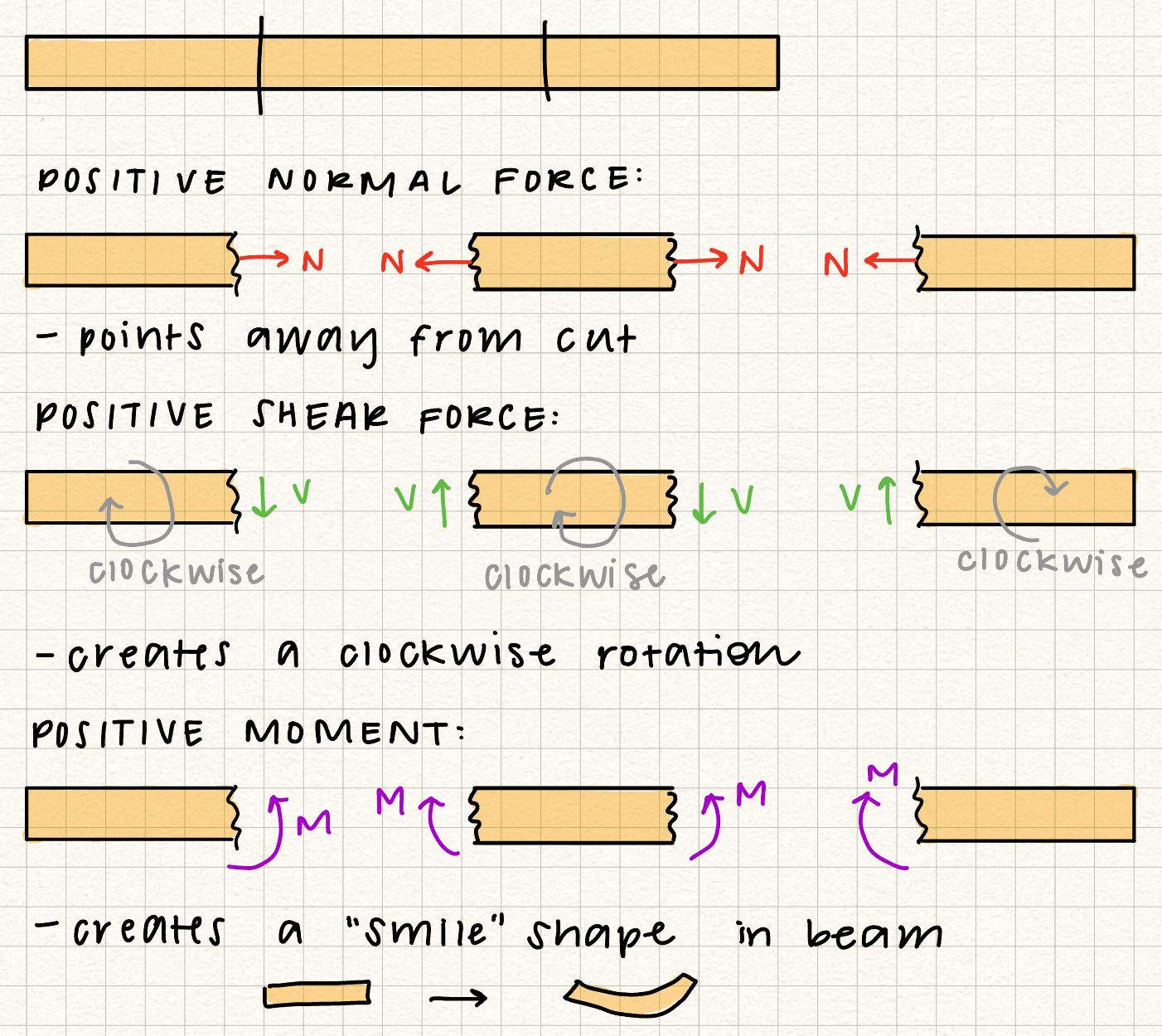
General procedure
Creating a shear force and bending moment diagram allows us to create a graphical representation of \( V \) and \( M \) as a function of the position along the beam, \( x \). Therefore when creating internal loading diagrams we are trying to write equations for \( V(x) \) and \( M(x) \).
The general procedures for creating shear / bending moment diagrams are:
- Find support reactions
- Specify the x-coordinates
- Divide the beam into regions: one region for every change in loading
- Analyze each region by cutting inside each region and analyzing the free body diagram of the left side of the cut
- Apply equations of equilibrium to solve for \(V\) and \(M\) as functions of x
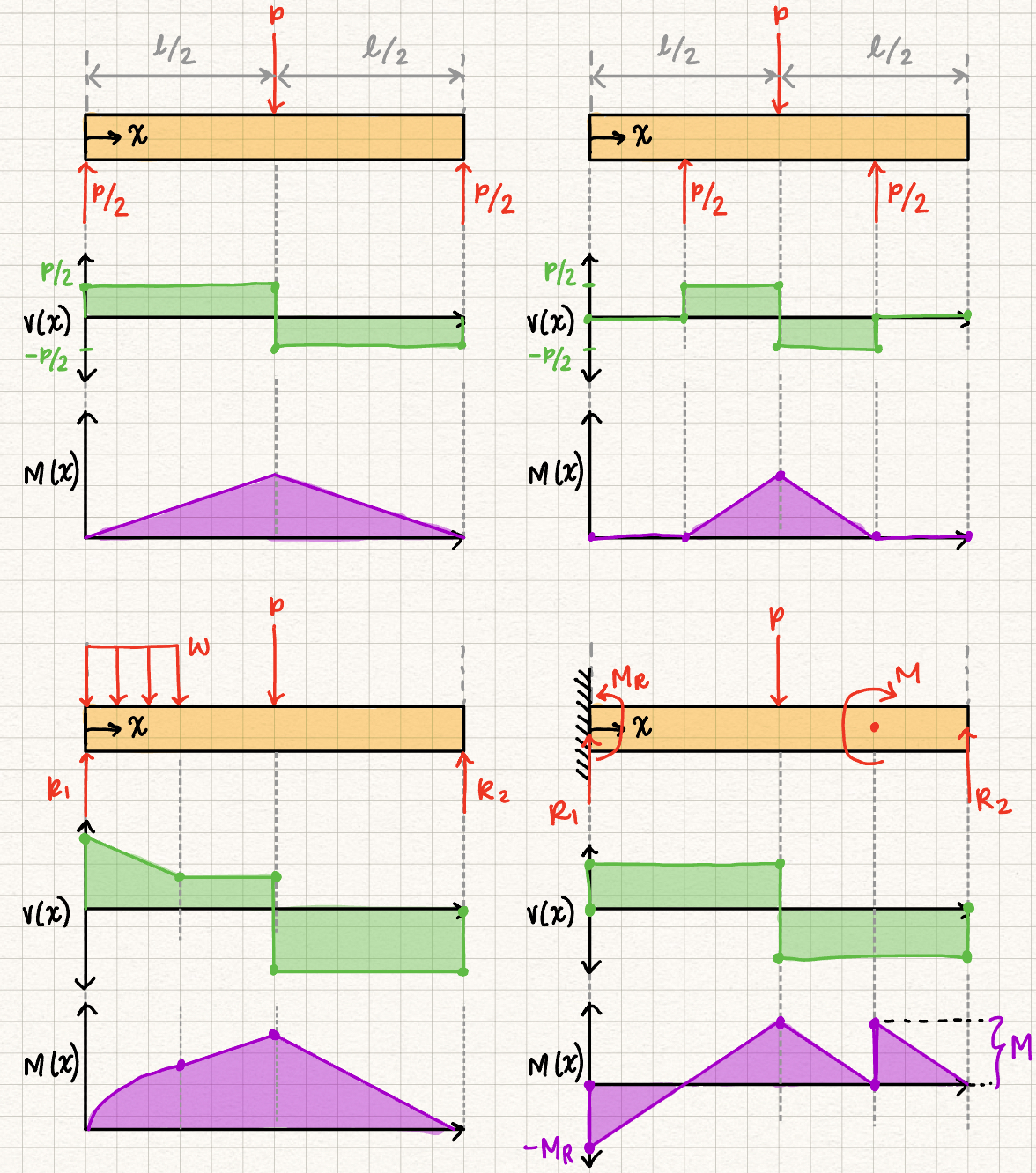
A note on concentrated moments
In our discussion on Equivalent Systems, we noted that you can move a couple moment anywhere on a rigid body with no external effect.
However, in this section we are concerned about the internal forces in a rigid body. When you move a concentrated moment, it changes the internal loading of the rigid body, so you have to leave the moment where it is to analyze the internal forces of a system.
General rules
- Concentrated external force or moment: there will be a "jump" in the shear force or bending moment diagram.
- Upward forces lead to an upward jump in \(V\) equal to the magnitude of the concentrated external force.
- Clockwise external moments result in a jump "up" in the graph of \(M\) equal to the magnitude of the concentrated external moment.
- Distributed external loads: \(w(x)\), \(V\), and \(M\) are related via the following relationship:
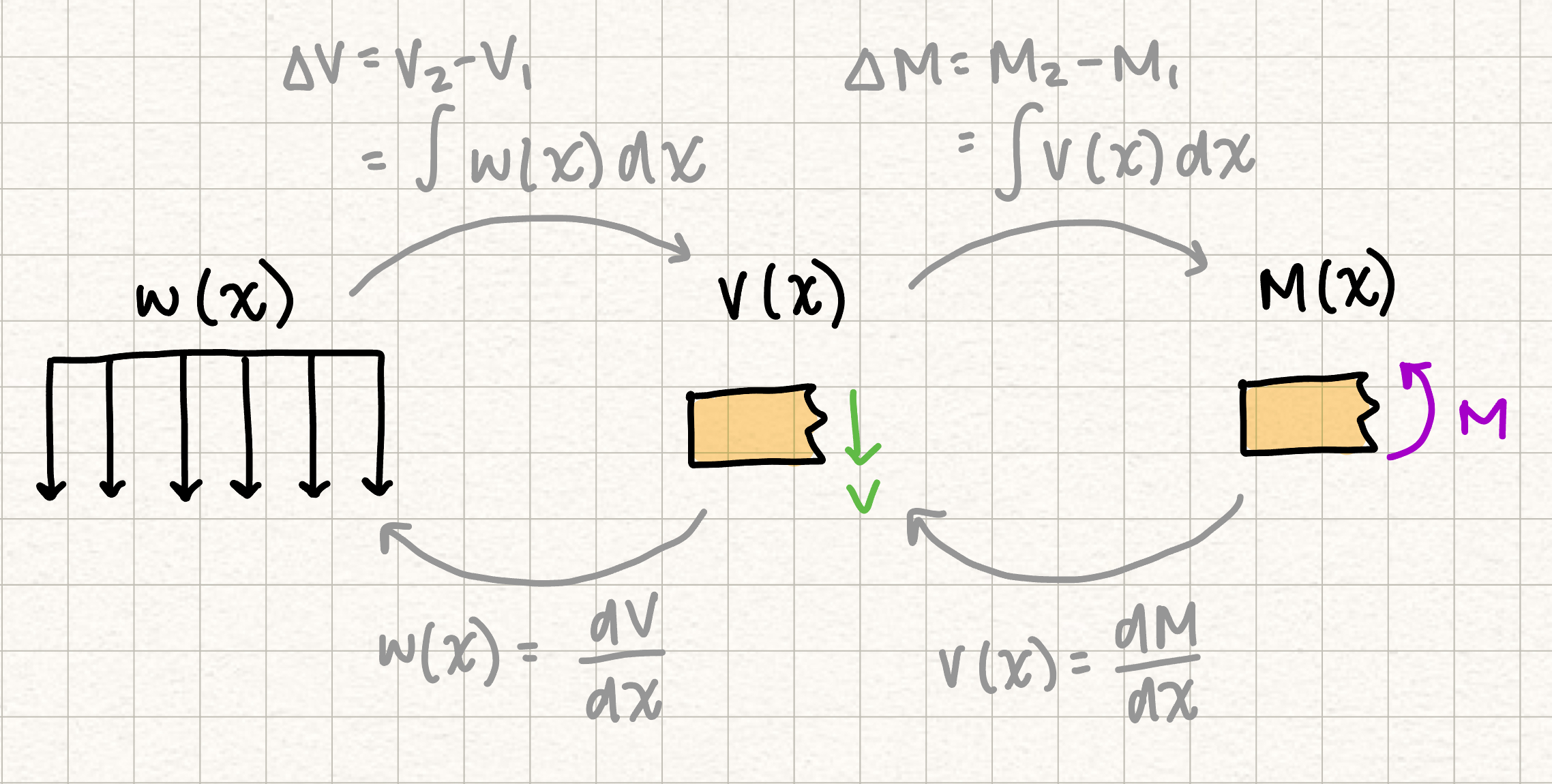
| Diagram | Jumps | Slope | Integral |
|---|---|---|---|
|
Internal shear force \( (V) \) |
(+) concentrated force \( \rightarrow \) (+) jump in internal shear force concentrated moment \( \rightarrow \) no effect | (-) internal shear slope | distributed load curve) |
|
Internal bending moment \( (M) \) |
(+, CCW) moment \( \rightarrow \) (-) jump in internal moment | (+) internal moment slope | shear force curve) |