Moment of inertia
Note: in statics we are using the second moment of area as our moment of inertia. In dynamics, a different moment of inertia is used (the mass moment of inertia). The differences between these two quantities are summarized in the following table.| Mass moment of inertia | Area moment of inertia (used in Statics!) | |
|---|---|---|
| Other names | Second moment of area | |
| Description | Determines the torque needed to produce a desired angular rotation about an axis of rotation (resistance to rotation) | Determines the moment needed to produce a desired curvature about an axis(resistance to bending) |
| Equations | | |
| Units | \( \mathrm{mass} \ \mathrm{length} ^ 2 \) | \( \mathrm{length} ^ 4 \) |
| Typical Equations | | |
| Courses | TAM 212 | TAM 210, TAM 251 |
Moment of inertia (second moment of area)
The moment of inertia used in statics is the "second moment of area". This is a mass property that determines the amount of torque that is needed to create an angular acceleration about a specific axis of rotation. The dimension of the area moment of inertia is \( \mathrm{length} ^ 4 \). Moment of inertia about the x-axis
Moment of inertia about the y-axis
Polar moment of inertia.
Parallel axis theorem
The parallel axis theorem is used to calculate the moment of inertia for an object around axes other than through the centroid.
Parallel axis theorem.
where \( I_{x'} \) and \( I_{y'} \) are the moments of inertia about the centroid, \( A \) is the total area of the shape, and \( d \) is the perpendicular distance from the centroid to the axes of interest in either the x or y directions.
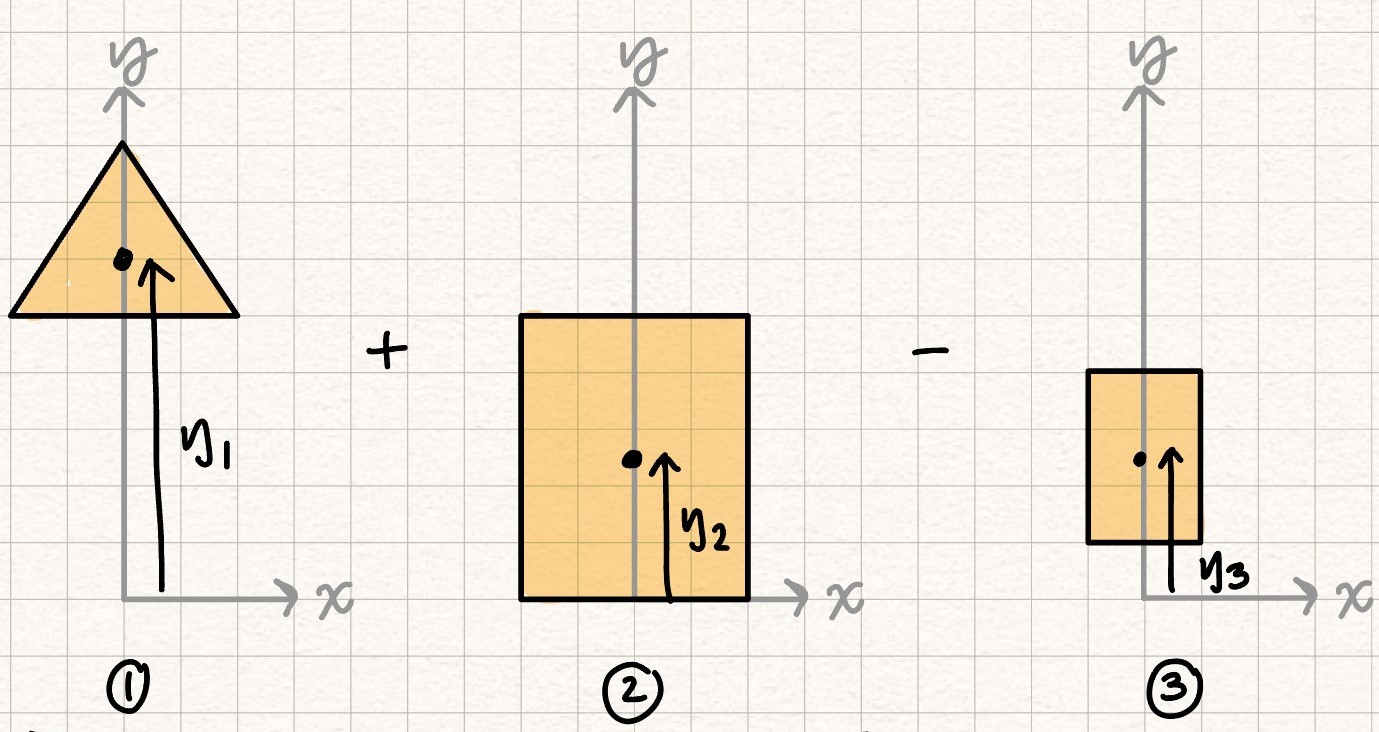
Combining moments of inertia
Moments of inertia of simple shapes can be combined to calculate the moments of inertia of more complex shapes using the parallel axis theorum.
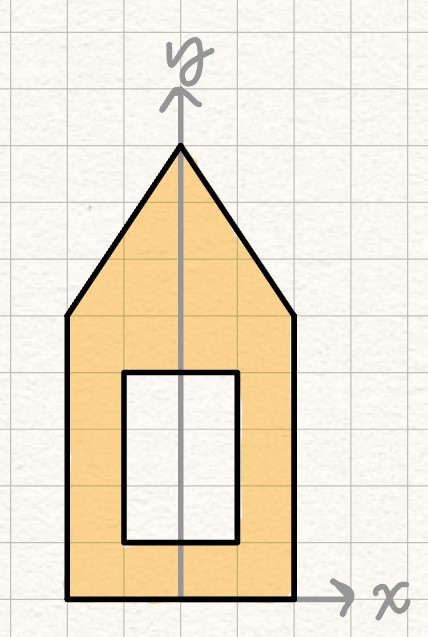
Example Problem: Find the moment of inertia of a composite shape. #blt-fst
Moment of inertia for typical shapes
| Shape | Diagram | MoI about the centroid (centroidal axis) | MoI about the origin |
|---|---|---|---|
| Rectangle | 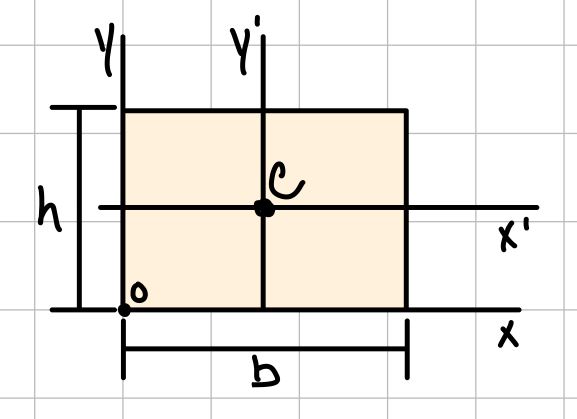 | \( \bar{I_{x'}} = \frac{1}{12}b h^3 \) \( \bar{I_{y'}} = \frac{1}{12}b^3 h \) \( J_c = \frac{1}{12}bh(b^2+h^2) \) | \( I_x = \frac{1}{3}b h^3 \) \( I_y = \frac{1}{3}b^3 h \) |
| Triangle | 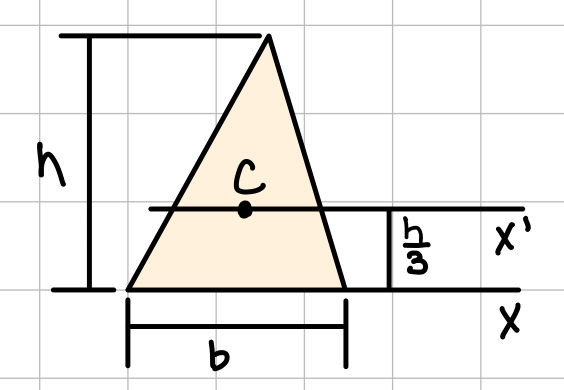 | \( \bar{I_{x'}} = \frac{1}{36}bh^3 \) | \( I_x = \frac{1}{12}bh^3 \) |
| Circle | 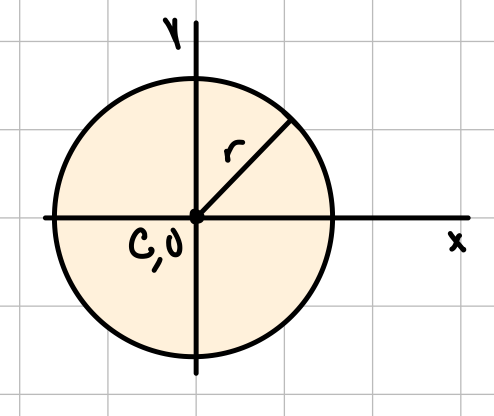 | \( \bar{I_{x'}} = \bar{I_{y'}} = \frac{1}{4} \pi r^4 \) | \( J_O= \frac{1}{2} \pi r^4 \) |
| Semicircle | 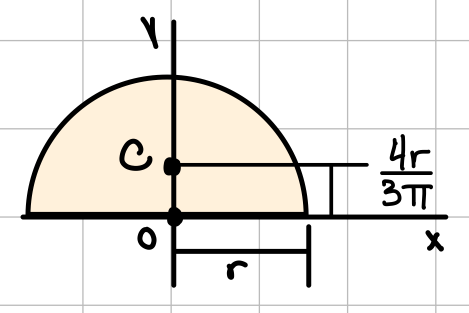 | \( \bar{I_{x'}} = (\frac{\pi}{8} - \frac{8}{9\pi}) r^4 \) \( \bar{I_{y'}} = \frac{\pi}{8}r^4 \) | \( I_x = I_y = \frac{1}{8} \pi r^4 \) \( J_O = \frac{1}{4} \pi r^4 \) |
| Quarter circle | 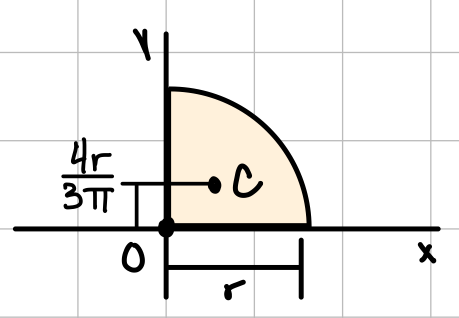 | \( \bar{I_{x'}} = \bar{I_{y'}} = \frac{1}{2}(\frac{\pi}{8} - \frac{8}{9\pi}) r^4 \) | \( I_x = I_y = \frac{1}{16} \pi r^4 \) \( J_O = \frac{1}{8} \pi r^4 \) |
| Ellipse | 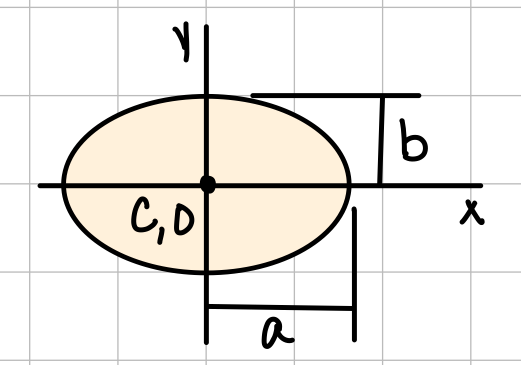 | \( \bar{I_{x'}} = \frac{1}{4} \pi a b^3 \) \( \bar{I_{y'}} = \frac{1}{4} \pi a^3 b \) | \( J_O = \frac{1}{4} \pi ab(a^2+b^2) \) |