Center of mass, gravity, and volume
The center of mass, center of gravity, and center of volume of an object are all very similar. In fact, they are all the same if the density of the object is constant and gravity is constant along an object.
The center of mass, center of gravity, and center of volume are all represented by a point \( (\bar{x},\bar{y}, \bar{z}) \).
| Center of Mass | Center of Gravity | Center of Volume (Centroid) | |
|---|---|---|---|
| Definition |
Average location of the mass of an object |
Average location of the weight of an object |
Geometric center of an object |
| Equation (Summation Form) | | | |
| Equation (Integral Form) | | | |
When are Centers of Gravity, Mass, and Volume the same? Deriving each will make this clearer.
Conclusion: the center of gravity, center of mass, and center of volume of an object are the same when that object has a constant density (is homogeneous) and gravity is constant along the object.
Centroid
The centroid denotes the geometric center of an object. When an object is made of a homogeneous material, the centroid and the center of mass are at the same point. If the object has an axis of symmetry, the centroid is on the axis of symmetry. In some cases, the centroid may not be on the object.
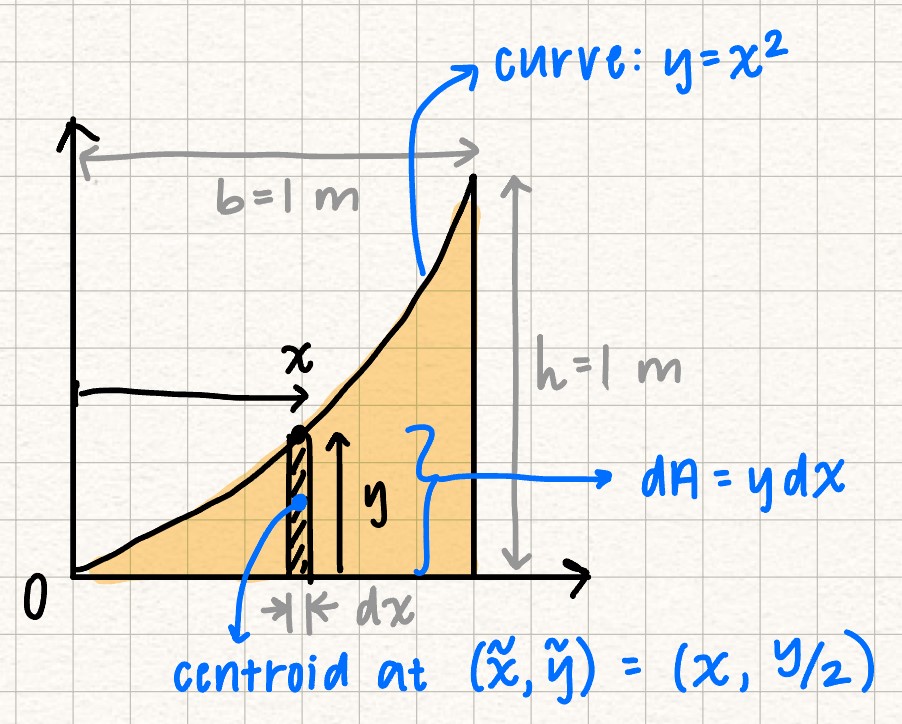
To solve for the centroid of an object:- Define your coordinate system
- Define the infinitesimally small element (usually \(dL\), \(dA\), or \(dV\))
- Express the element in terms of the coordinate system you defined
- Identify any symmetry
- Define the centroid \( (\tilde{x}, \tilde{y}) \)of the element
- Plug the equations from 3 and 5 into the equations for the centroid
The equation for the centroid of an object is:
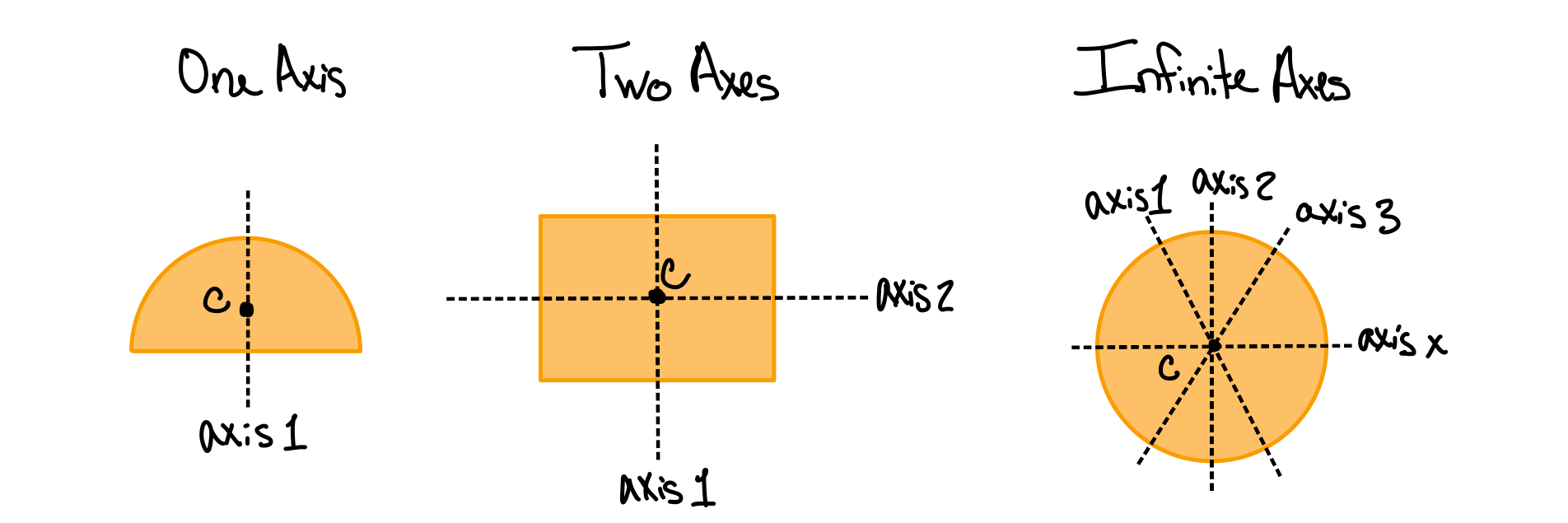
Axes of symmetry
Centroids of basic shapes
| Shape | Diagram | ||
|---|---|---|---|
| Rectangle | 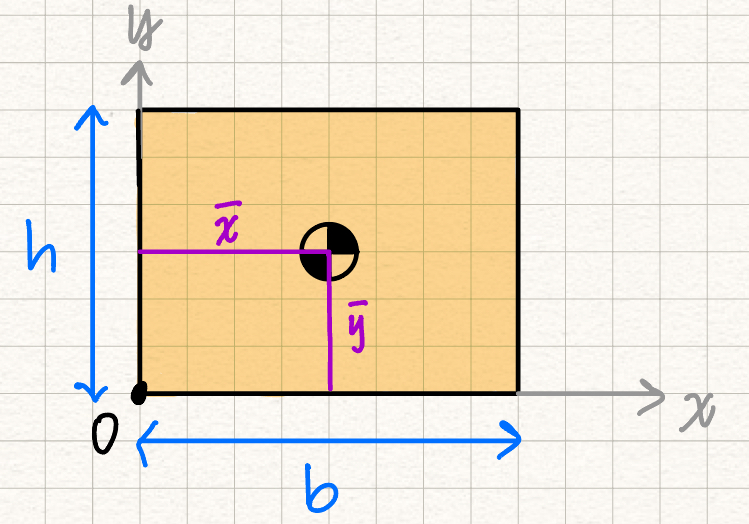 | ||
| Right Triangle | 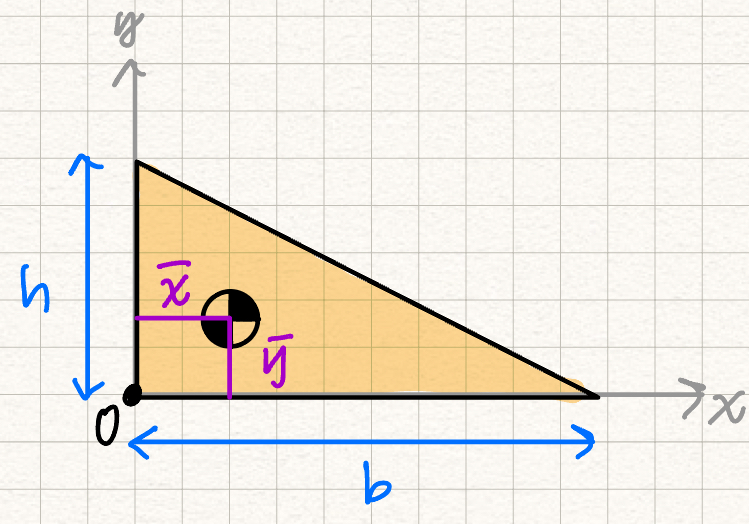 | ||
| Isoceles Triangle | 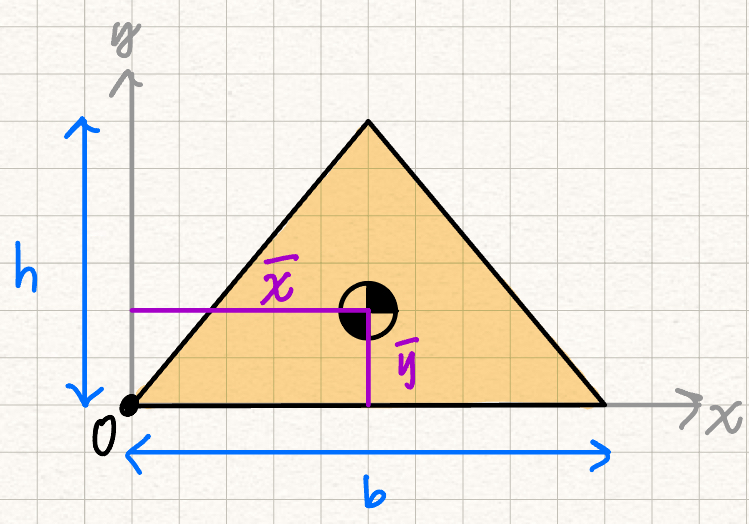 | ||
| Circle | 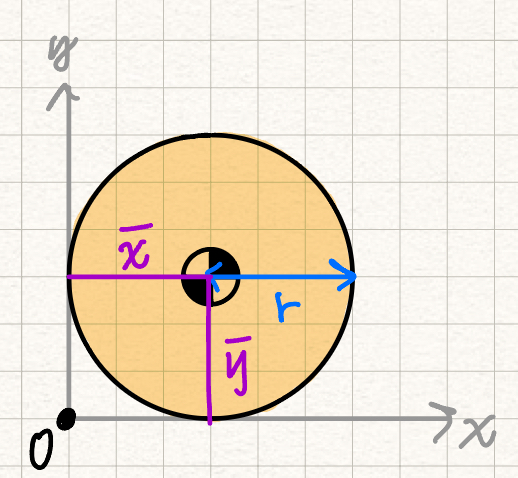 | ||
| Semicircle | 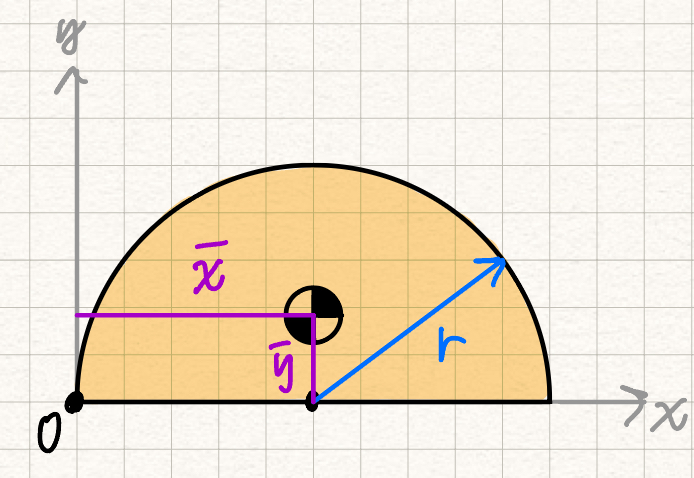 | ||
| Quarter Circle | 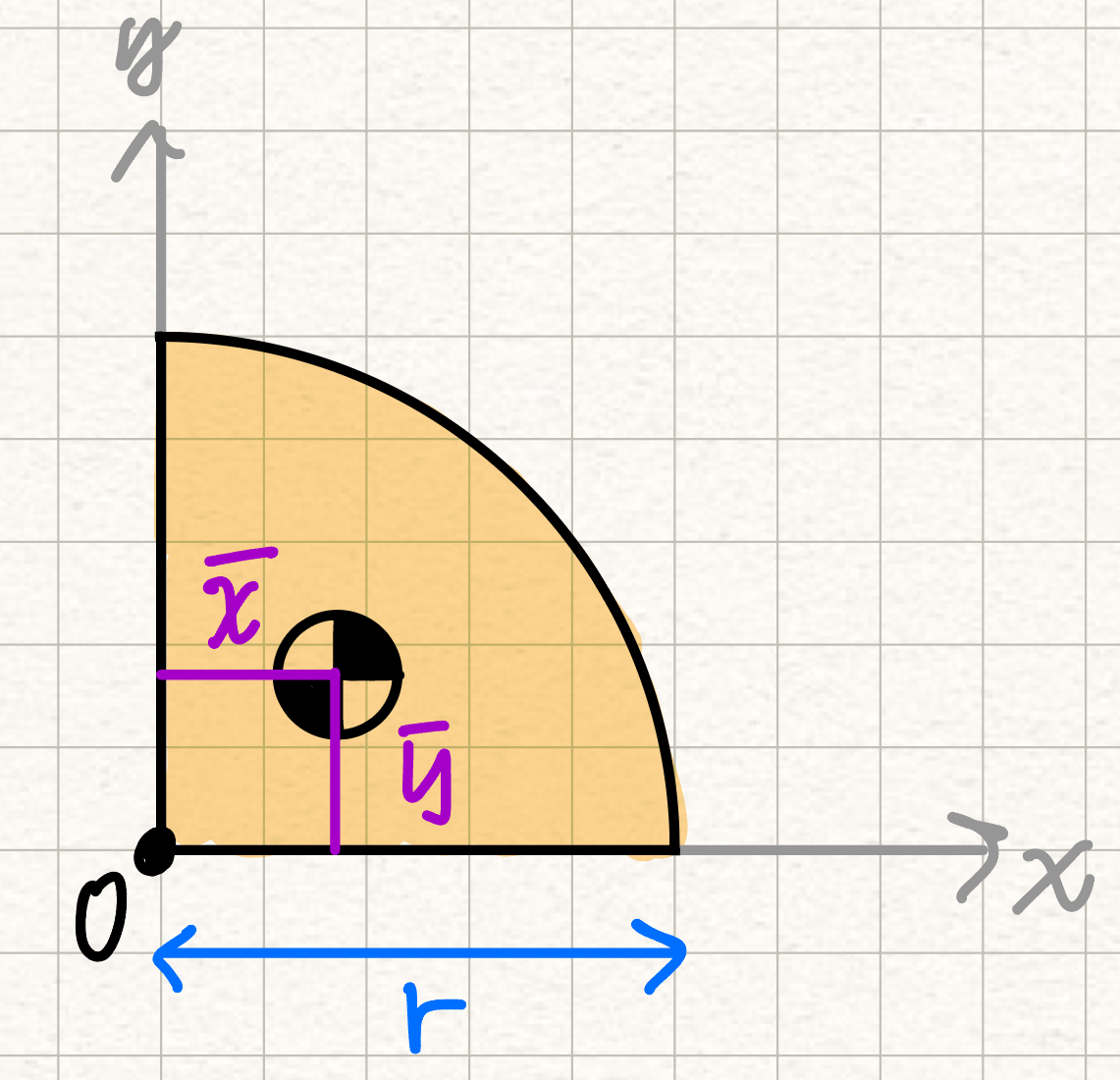 |
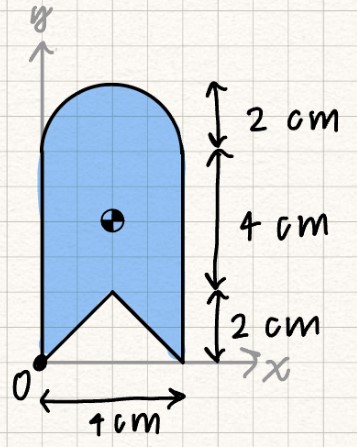
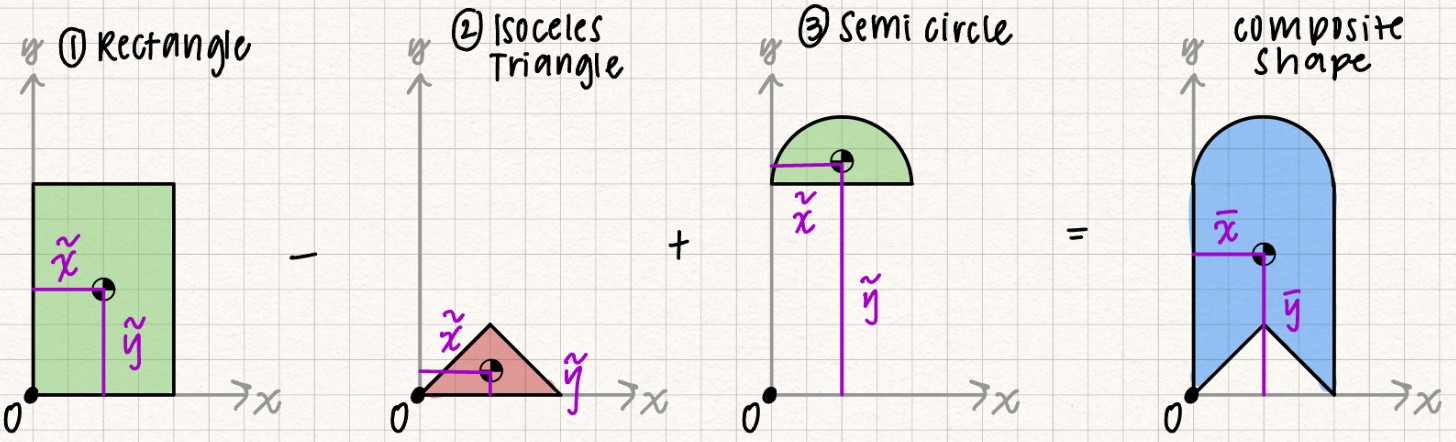
Finding centroids using composite shapes
We can find the centroid of more complicated shapes by breaking them up into simpler shapes and finding the centroids of those simpler shapes.
To solve for the centroid of our original shape \( (\bar{x}, \bar{y}) \), we take a weighted sum of each of the centroids of our smaller shapes. We will call the centroid locations of the smaller shapes \( \tilde{x} \) and \( \tilde{y} \).
For these equations, the weighted sum is dependent on the area of each individual shape. This is typically for 2D problems. You can also use length, weight, or mass as your weighing factor depending on what you're being asked to solve for.