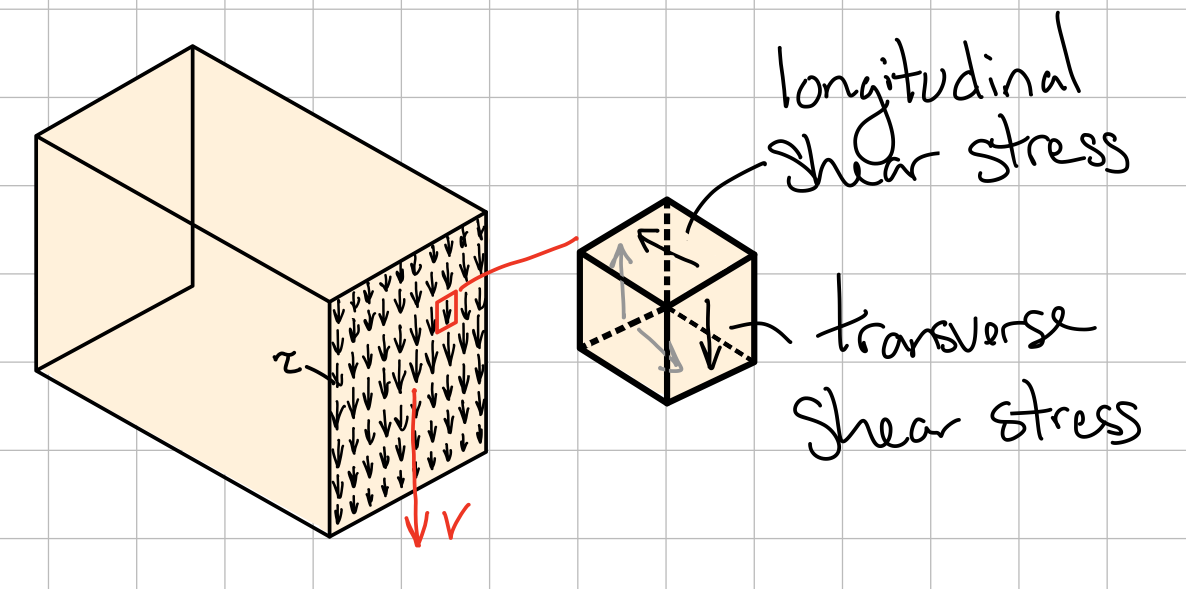
Transverse Shear
Shear Stress in Beams
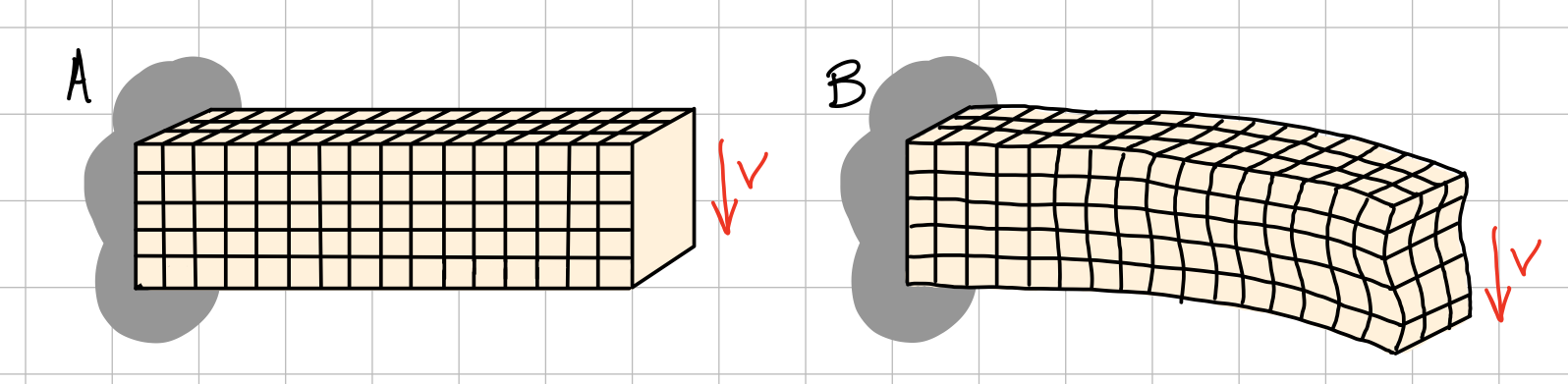
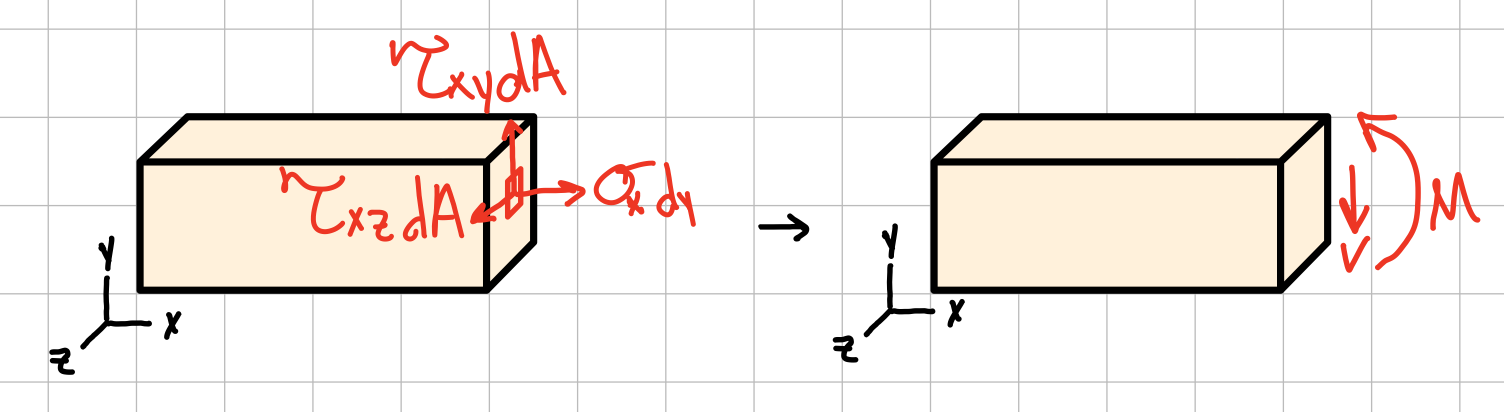
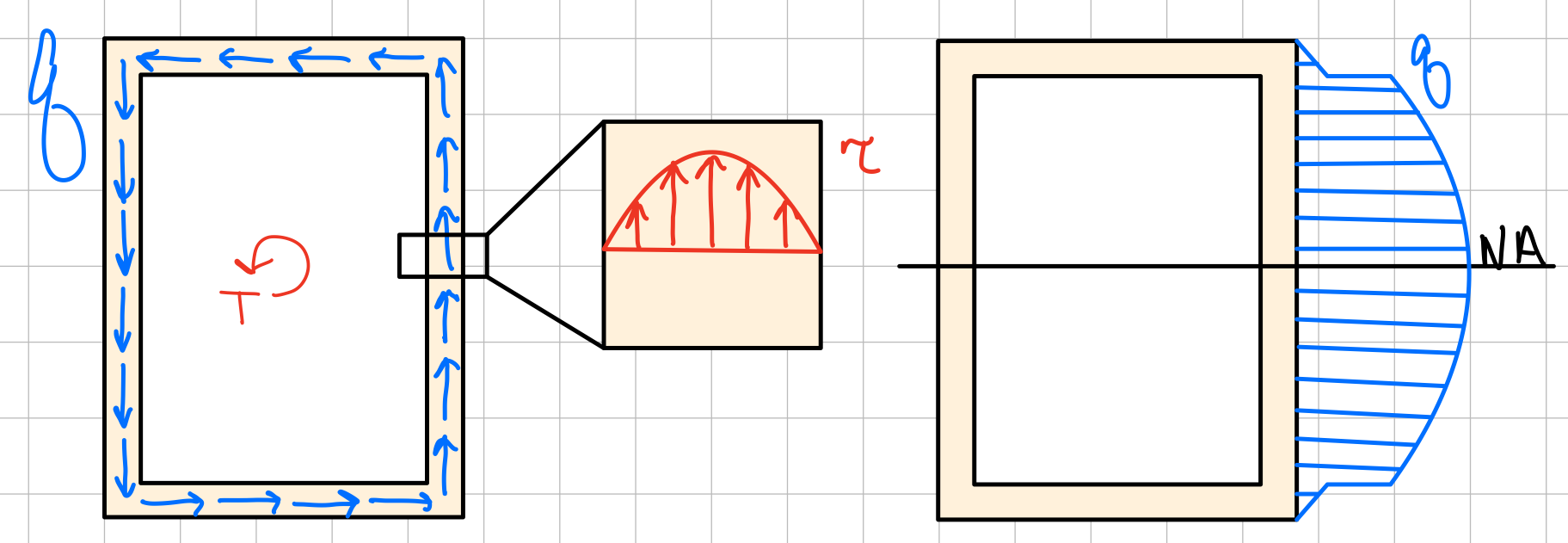
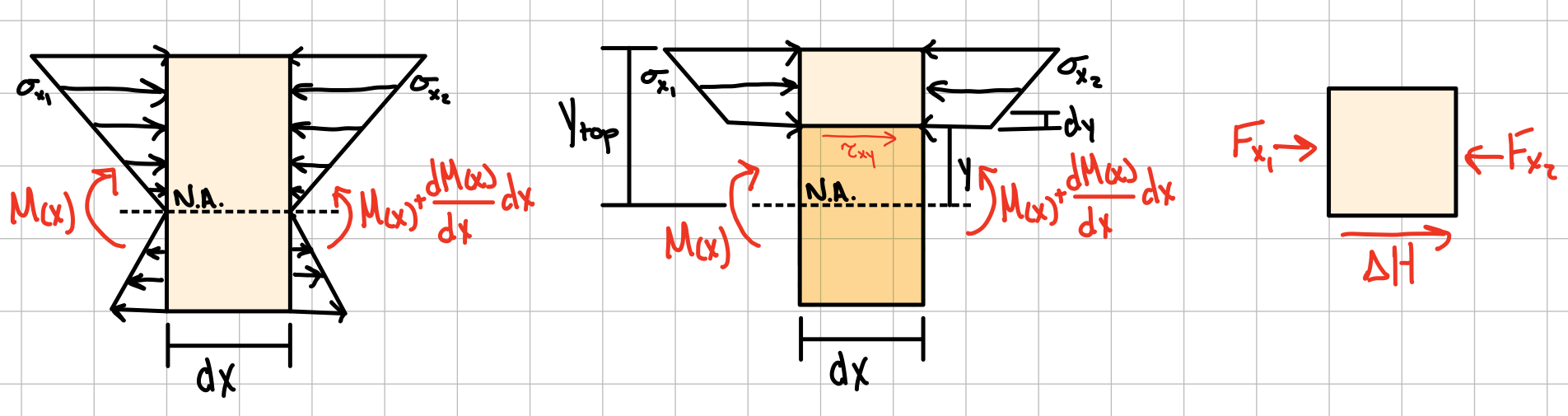
Equilibrium.
Symmetry of stress: transverse xy stress implies longitudinal yx stress.
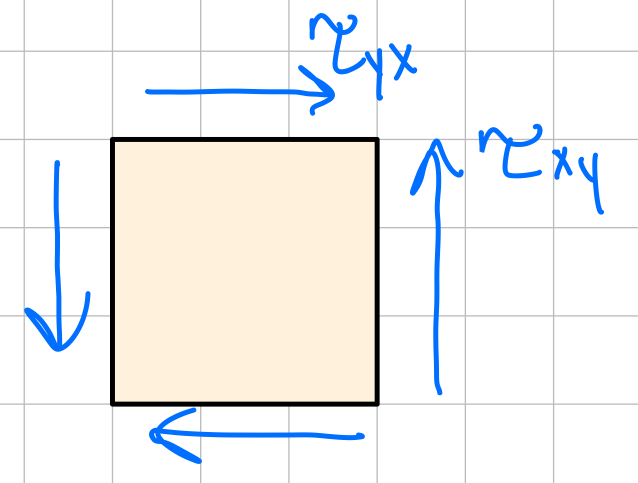
Symmetry.
Average Shear Stress
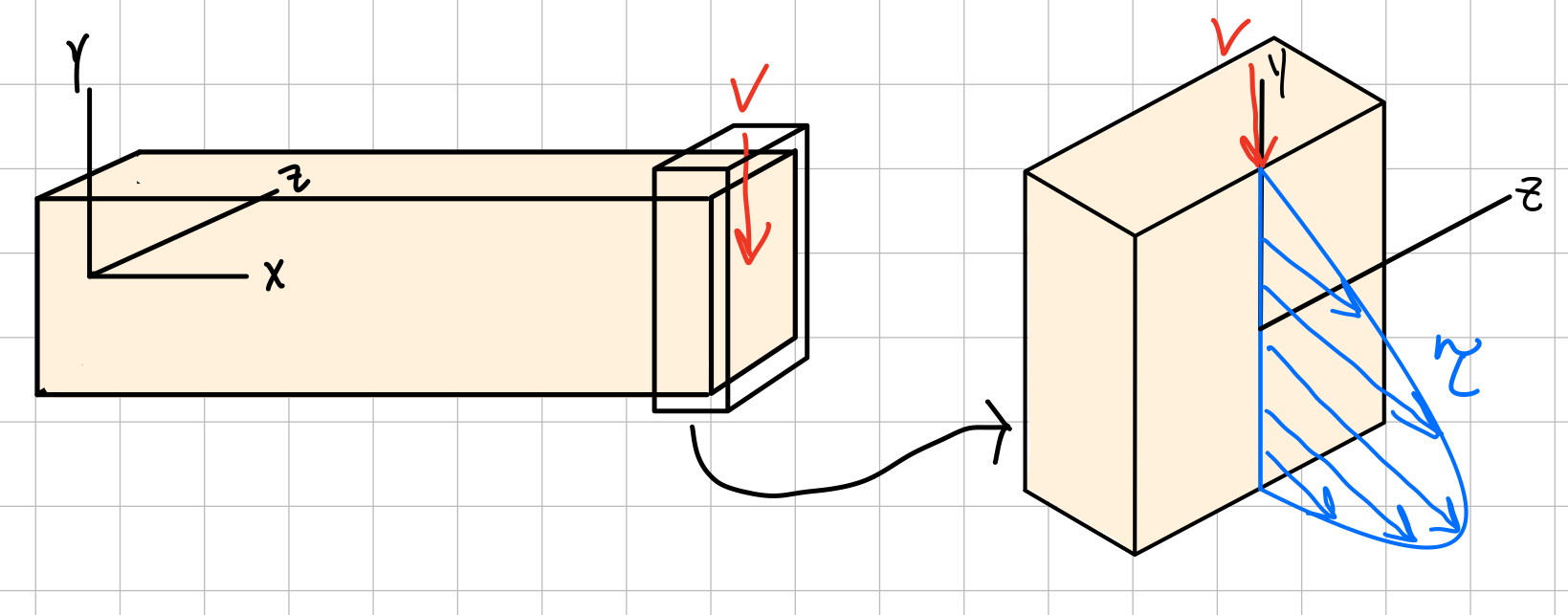
Avg. shear stress.
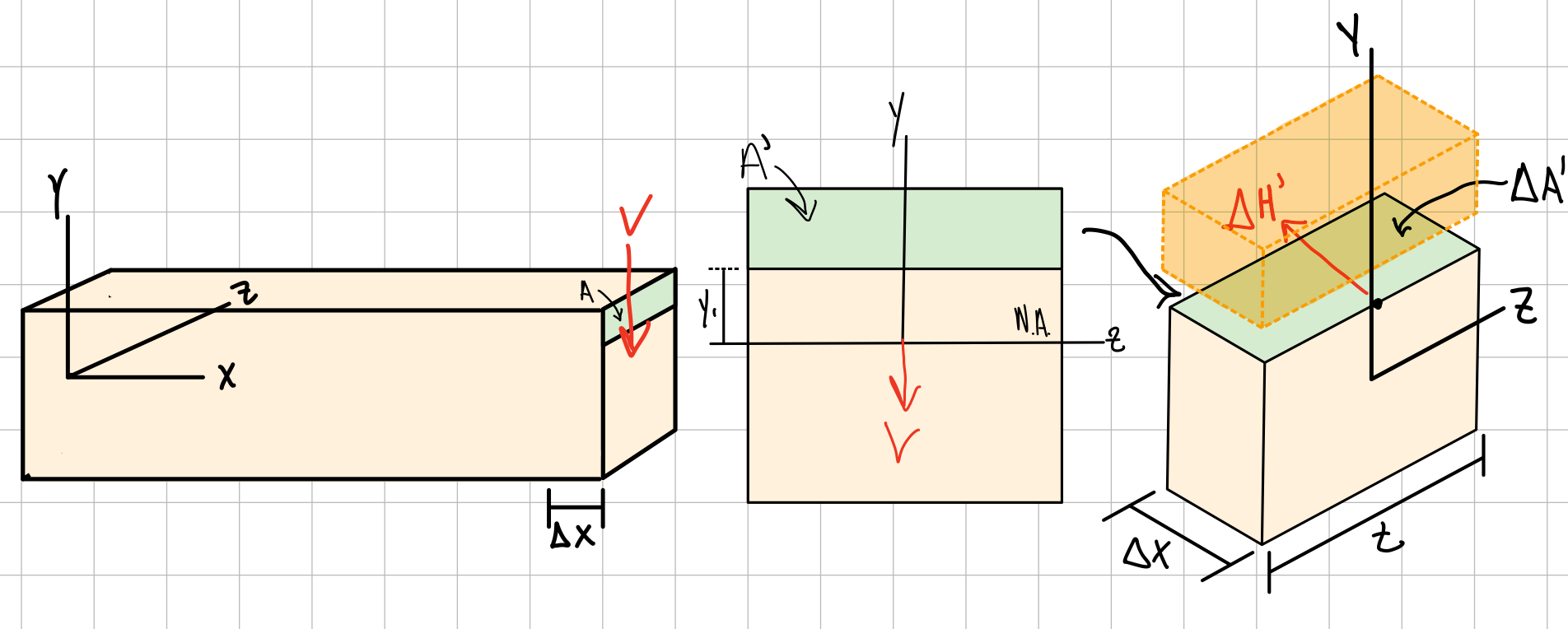
shear stress at a point. #shr-pts
- \( V \) : shear force
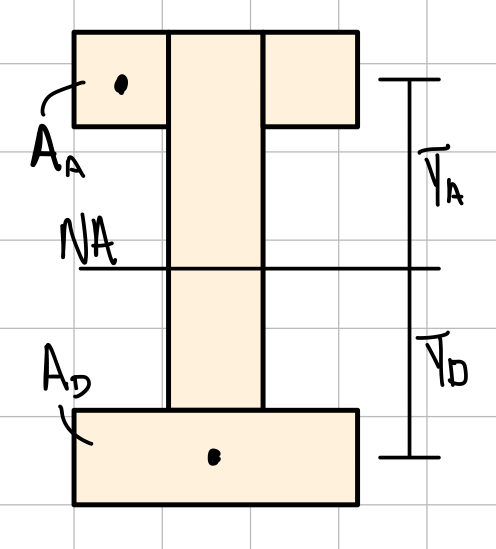
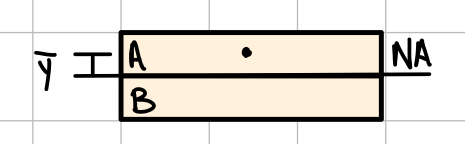
- \( Q \) : First area moment of inertia of cut section ( \( Q = \Sigma \bar{y}'A' \) )
- \( I \) : Second area moment of inertia of whole cross-sectional area
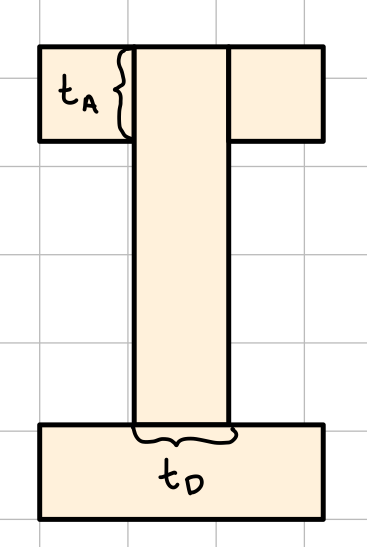
- \( t \) : beam thickness
Rectangular Beam Cross-Section
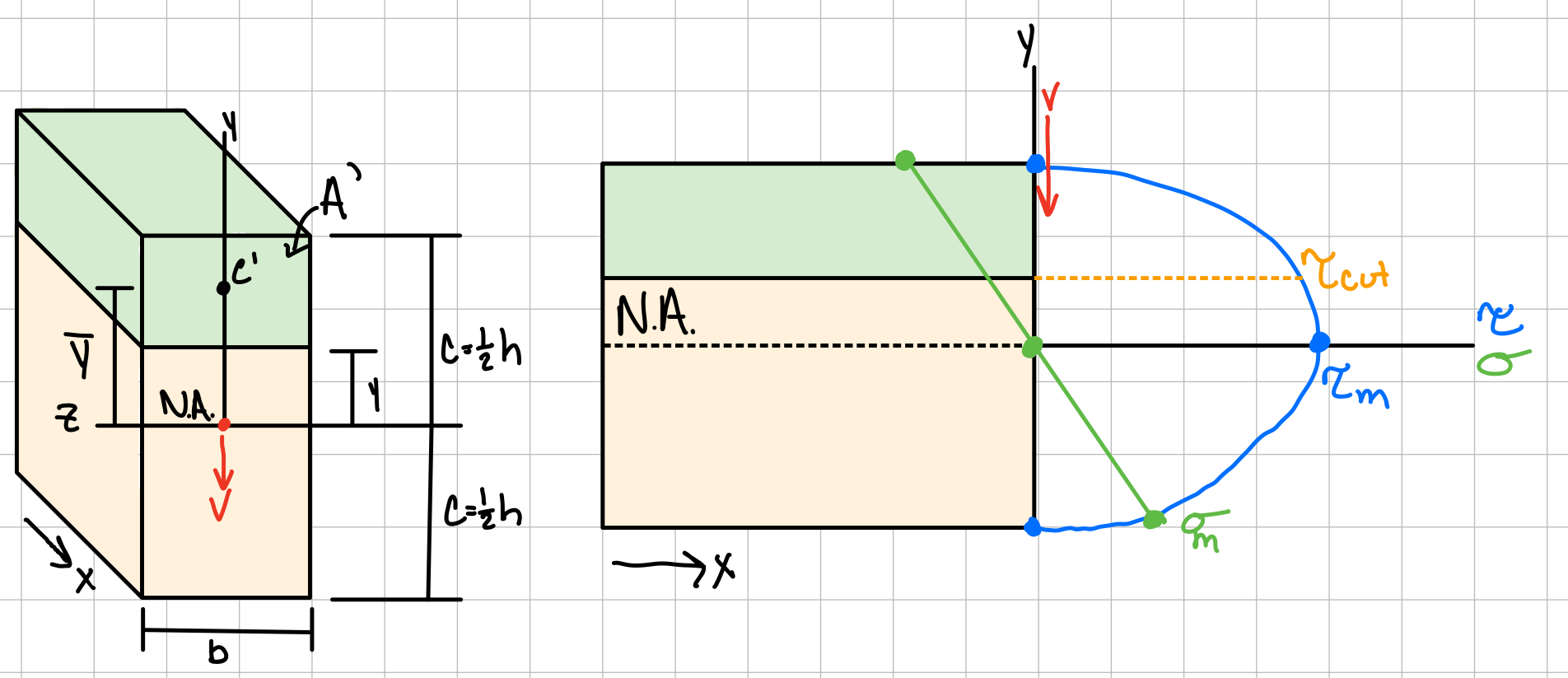
Shear stress at a given point (y) in a rectangular beam. #shr-rct
Max. shear stress in rectangular beam.
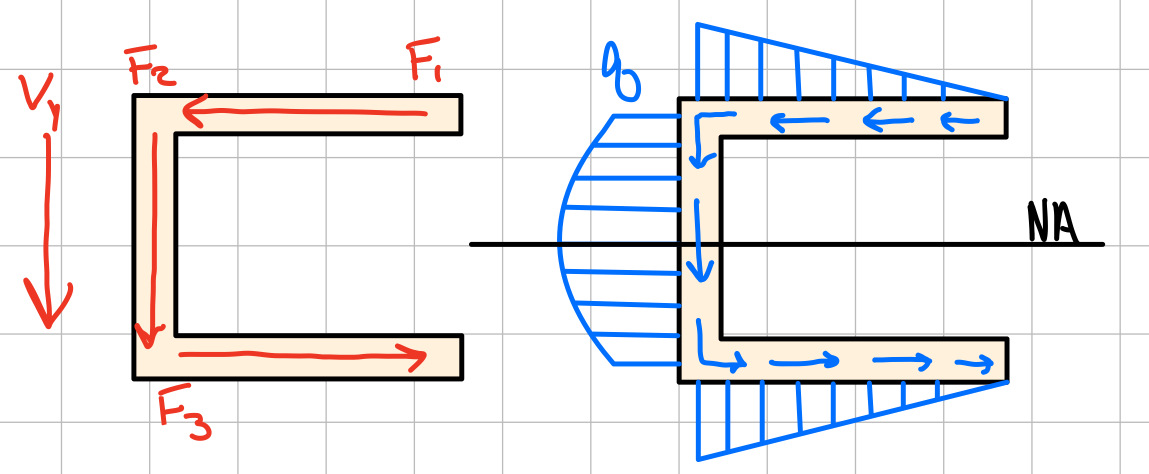
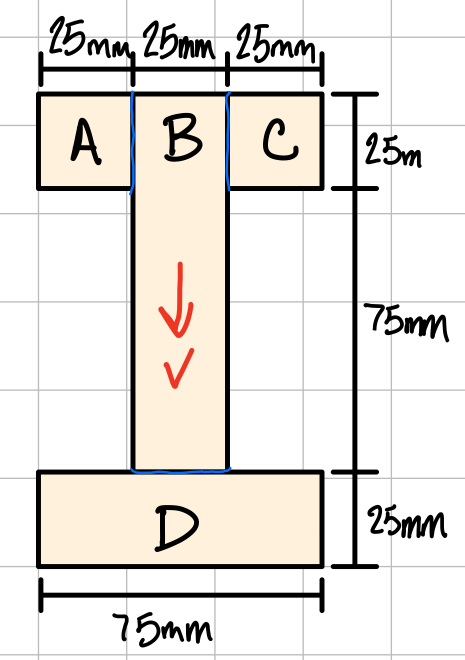
I-Shaped Beam Cross-Section
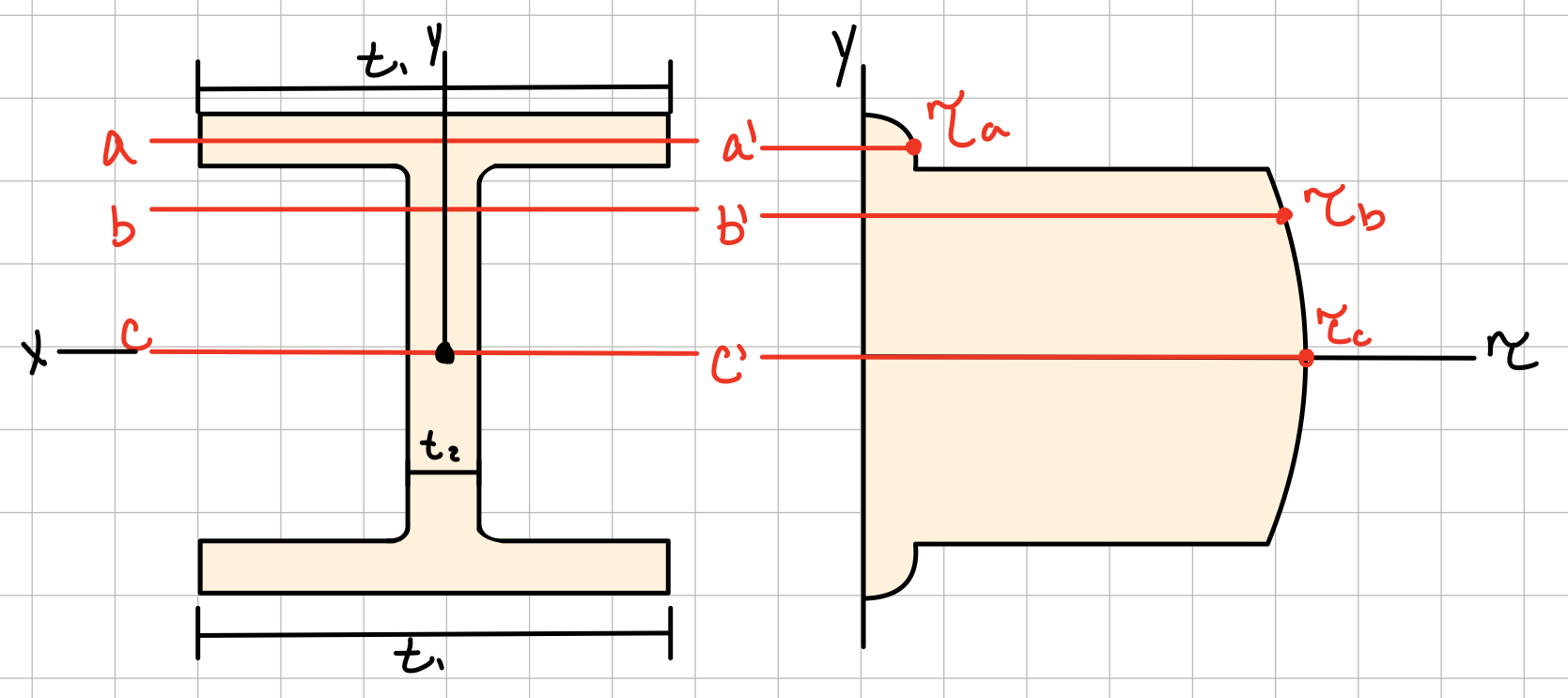
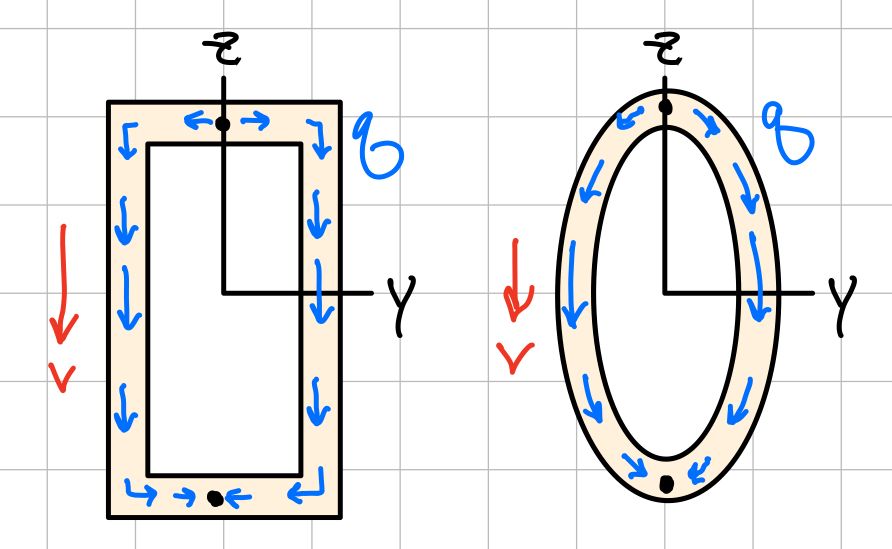
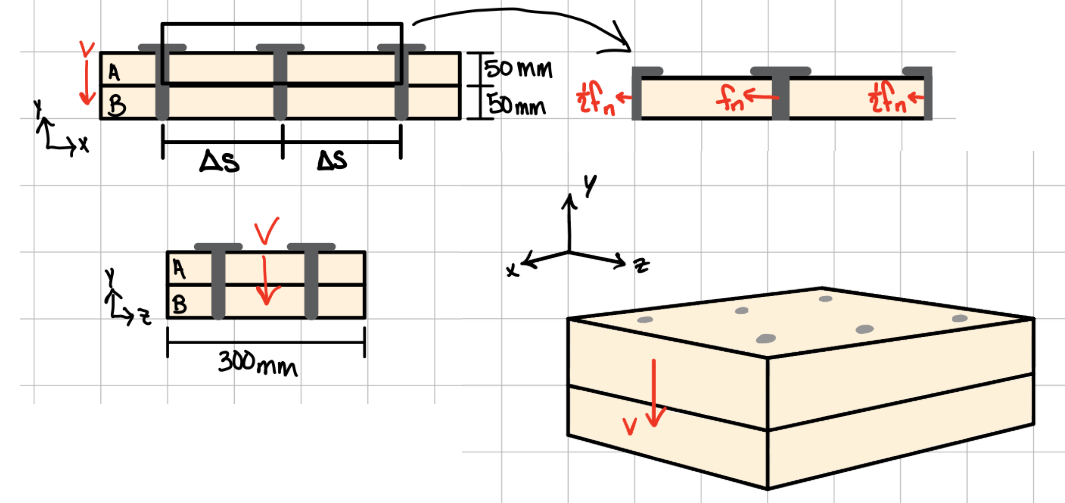
Built-up Members/Beams: Shear Flow
In some cases, it is more useful to look at shear flow (\( q \)) through a structure than internal shear stress.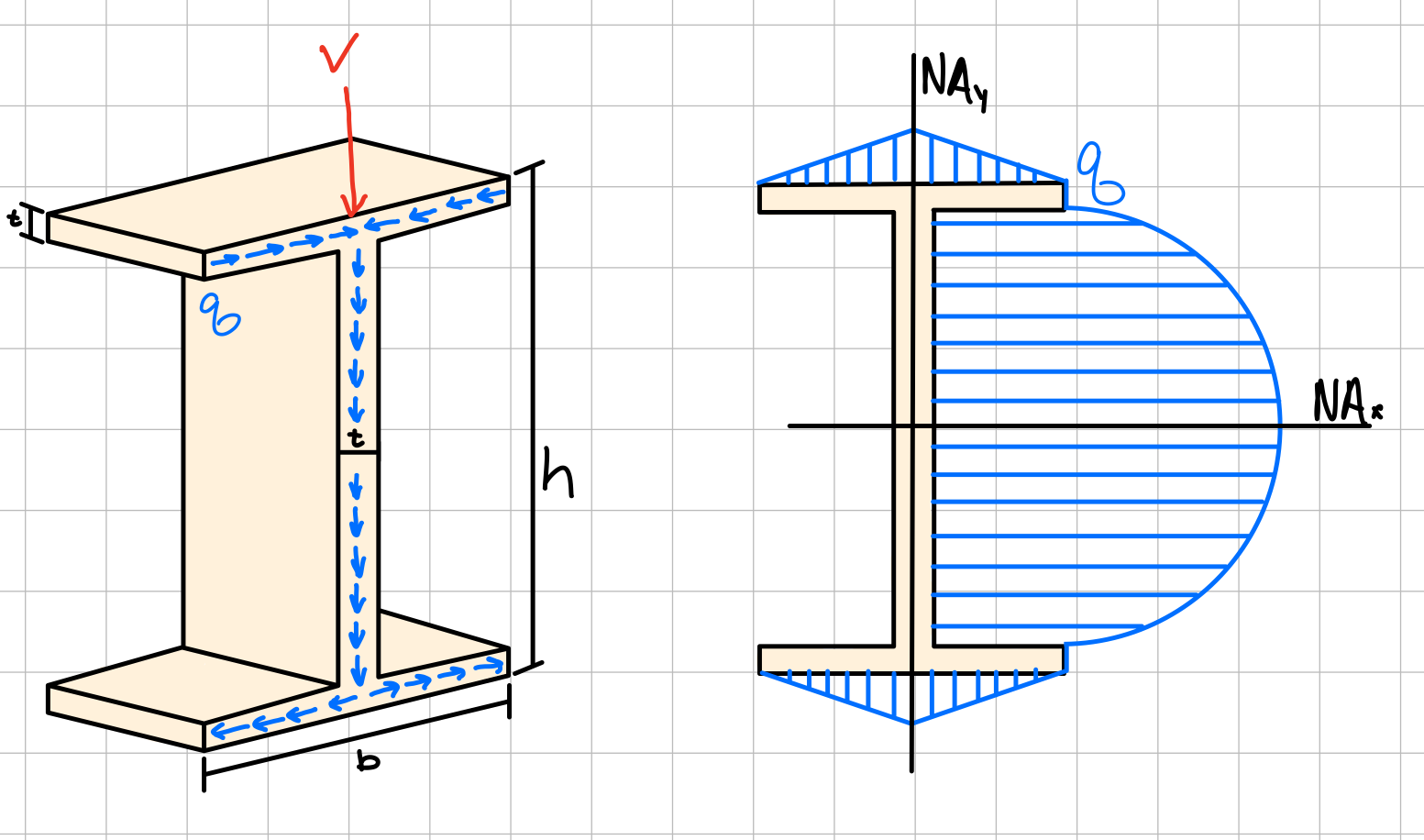
L: Shear flow direction. R: Shear flow magnitude
Shear flow (q). #shr-flw
Shear stress using shear flow.
For uniformly spaced fasteners:
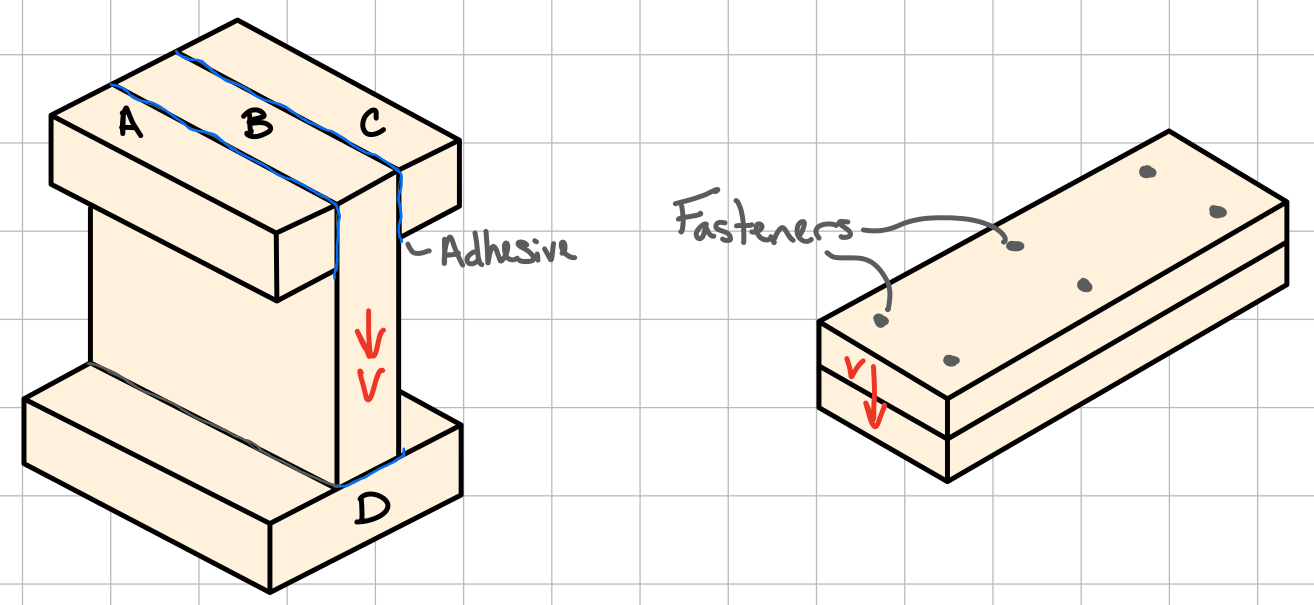
Adhesives supply resistance along the length of the contacting parts. Determine the minimum shear strength at these contacting/weak points using the shear stress equation.
Example Problem: The following I-beam is composed of 4 boards glued together #blt-adh
Fasteners supply resistance at fixed intervals. Use the shear flow formula to analyze the beam.
Example Problem: The following beam is composed of 2 boards connected by 6 nails. #blt-fst
Heads up!
shear stresses in thin-walled members builds on this content.