Reference Pages
Mechanical Engineering

    Scroll back to top

    Stress

    The internal forces and moments generally vary from point to point. Obtaining this distribution is of primary importance in mechanics of materials. The total force in a cross-section, divided by the cross-sectional area, is the stress. We use stress to normalize forces with respect to the size of the geometry.

    General stress tensor.
    $$ T= \begin{bmatrix} \sigma_{x} & \tau_{xy} & \tau_{xz} \\ \tau_{yx}& \sigma_{y} & \tau_{yz} \\ \tau_{zx}&\tau_{zy}&\sigma_{z} \end{bmatrix} \ $$
    Similarly to strain, all of the stress components acting on a point can be represented through a tensor.

    Stress under general loading conditions

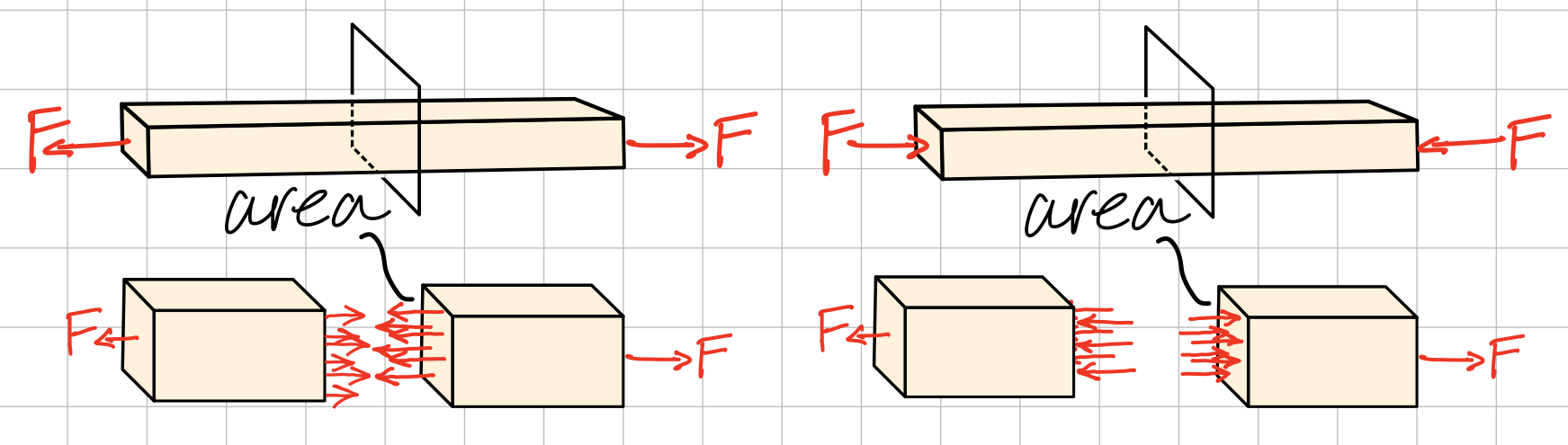
    We consider a homogeneous distribution of the internal force \( \Delta F \) over an infinitesimal area \( \Delta A \). The stress is defined by the infinitesimal force divided by the infinitesimal area.
    • Normal Stress: Defined by the intensity of the force acting NORMAL to \( \Delta A \)
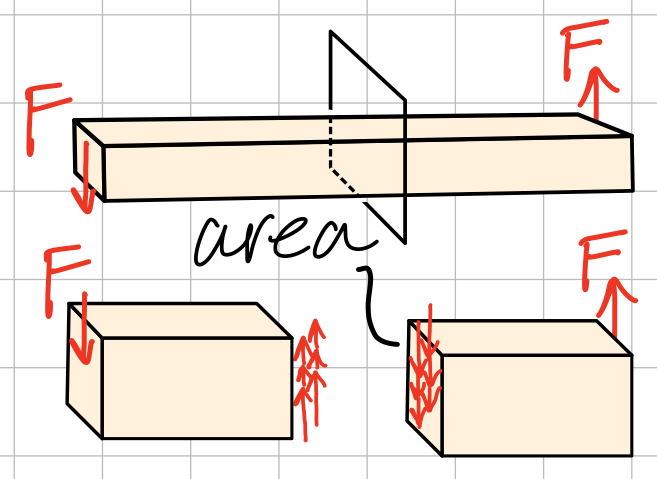
    • Shear Stress: Defined by the intensity of the force acting TANGENT to \( \Delta A \)

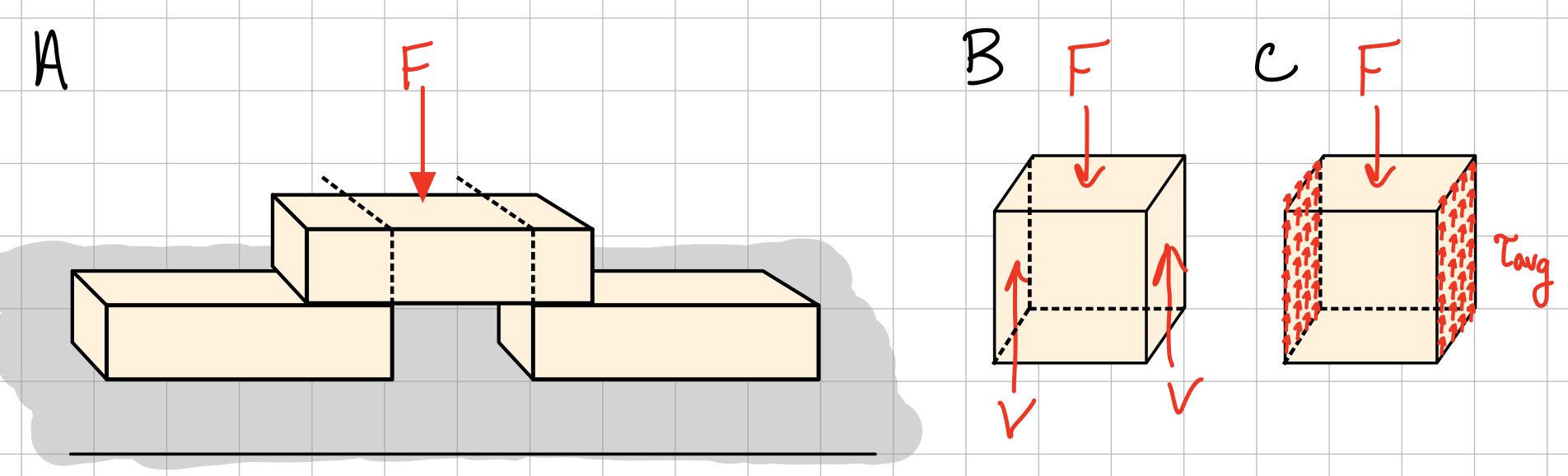
    Average Normal Stress - Axial Loading

    The normal stress components are represented by the values along the diagonal of the stress tensor.
    Normal stress tensor.
    $$ T= \begin{bmatrix} \sigma_{xx} & - & - \\ - & \sigma_{yy} & - \\ - & - & \sigma_{zz} \end{bmatrix} \ $$
    Normal stress
    Here we assume that the distribution of normal stresses in an axially loaded member is uniform. Stress is calculated away from the points of application of the concentrated loads. Uniform distribution of stress is possible only if the line of action of the concentrated load \( P \) passes through the centroid of the section considered
    Average normal stress. #avn-sts
    $$ \sigma_{ave} = \frac{F}{A}\ $$
    where \( F \) is the internal resultant normal force and \( A \) is the cross-sectional area of the bar where the normal stress \( \sigma_{ave} \) is calculated.
    Notation
    Around the point where the load is applied, the stress distribution is non-uniform. Cross-sections farther away from the point load gradually have a more uniform distribution. When the distance is greater than the widest dimension of the cross-section (\( l > b \)), the stress distribution is uniform.

    Average Shear Stress

    The shear stress components make up the rest of the tensor, consisting of all the components other than the ones on the diagonal.
    Shear stress tensor.
    $$ T= \begin{bmatrix} - & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & - & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & - \end{bmatrix} \ $$
    Shear stress
    Obtained when transverse forces are applied to a member. The distribution of shear stresses cannot be assumed uniform. Common in bolts, pins and rivets used to connect various structural members.
    Average shear stress
    Average shear stress. #avs-sts
    $$ \tau_{ave} = \frac{V}{A}\ $$
    where \( V \) is the internal resultant shear force and \( A \) is the cross-sectional area of the bar where the shear stress \( \tau_{ave} \) is calculated.
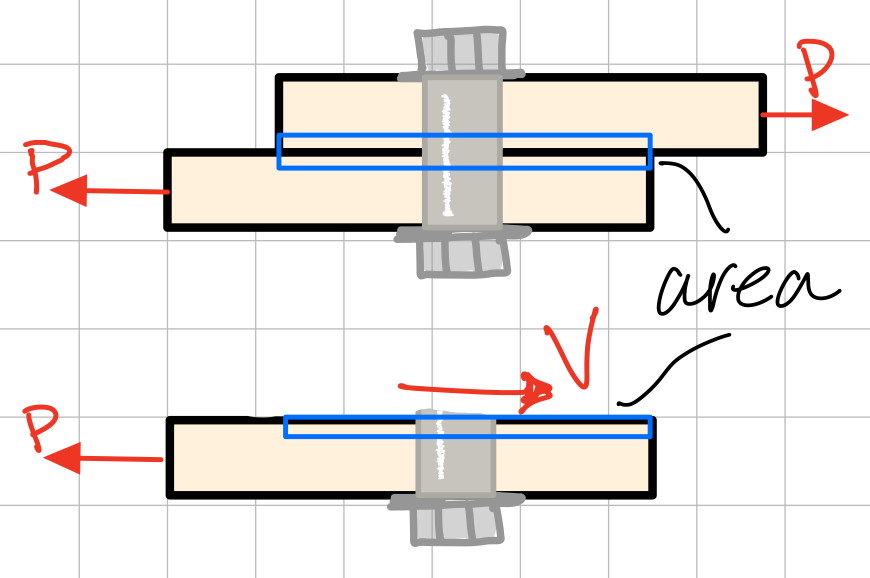
    Example Problem: Single shear: determine the shear stress in the bolt #sgl-shr

    Create the equilibrium equation and solve.

    $$ \Sigma F_y = V-P = 0\ $$
    $$ V = P\ $$
    $$ \tau_{ave} = \frac{P}{A}\ $$

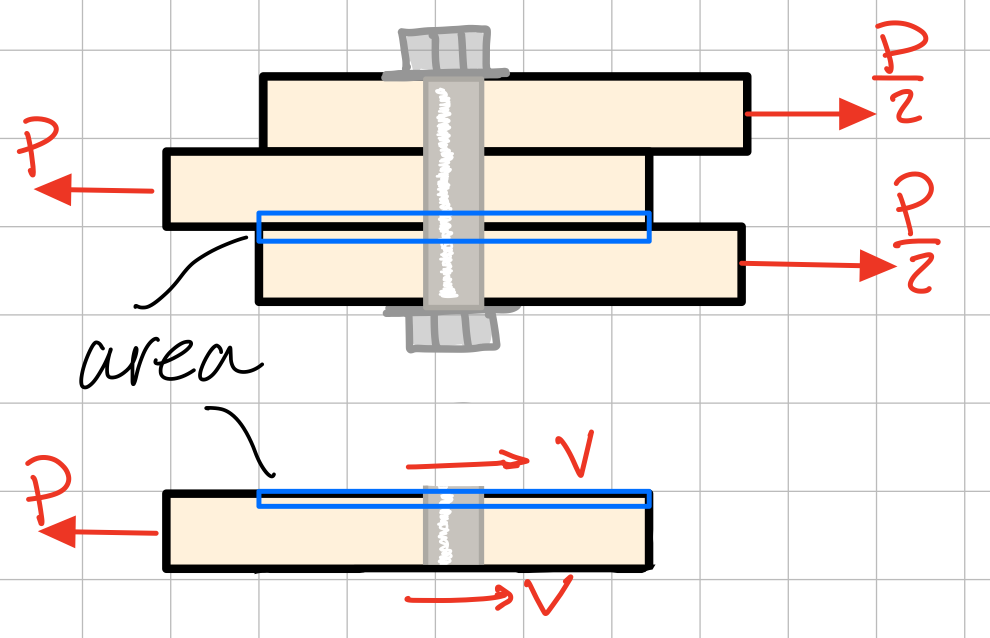
    Example Problem: Double shear: determine the shear stress in the bolt #dbl-shr

    Create the equilibrium equation and solve.

    $$ \Sigma F_y = 2V-P = 0\ $$
    $$ V = \frac{P}{2}\ $$
    $$ \tau_{ave} = \frac{P}{2A}\ $$

    Extra!

    Supplemental video:

    General State of Stress

    The general state of stress at a point is characterized by three independent normal stress components and three independent shear stress components, and is represented by the stress tensor. The combination of the state of stress for every point in the domain is called the stress field.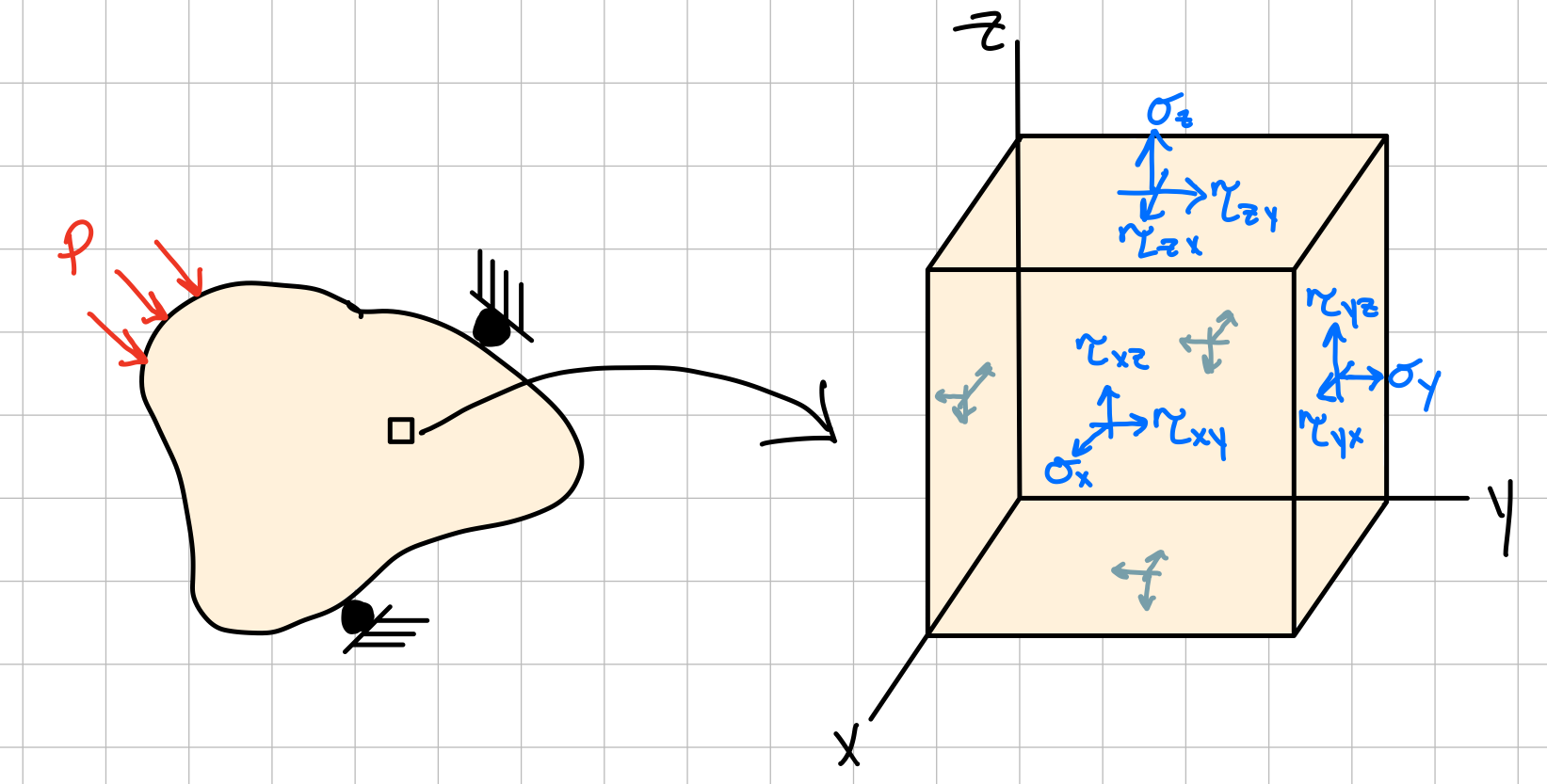
    Stress tensor.
    $$ T = \begin{bmatrix} \sigma_{x} & \tau_{xy} & \tau_{xz} \\ \tau_{xy} & \sigma_{y} & \tau_{yz} \\ \tau_{xz} & \tau_{yz} & \sigma_{z} \end{bmatrix} $$
    • Three normal stress components: \( \sigma_x, \sigma_y, \sigma_z \)
    • Six shear stress components: \( \tau_{xy} =\tau_{yx}, \tau_{xz}=\tau_{zx}, \tau_{yz}=\tau_{zy} \)
    The first subscript describes the surface orientation in the normal direction. The second subscript describes the direction of the stress.
    Warning: Stress is a physical quantity and as such, it is independent of the chosen coordinate system. #str-ind

    Heads up!

    Stress tensor builds on this content later in the course.

    Learn more about this topic on the Stress Transformation page.