Failure Theories
Failure of a material depends on (1) nature of loading and (2) type of material. There are theories that can predict material failure for complex states.Maximum Shear Stress (Tresca) Criterion
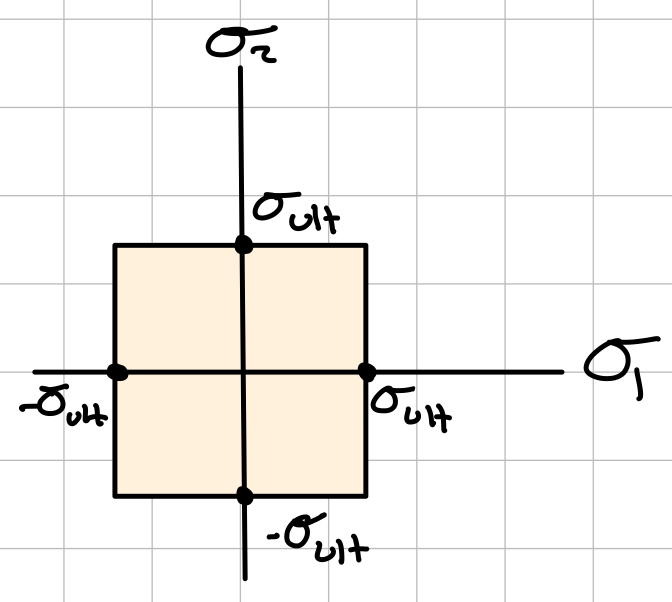
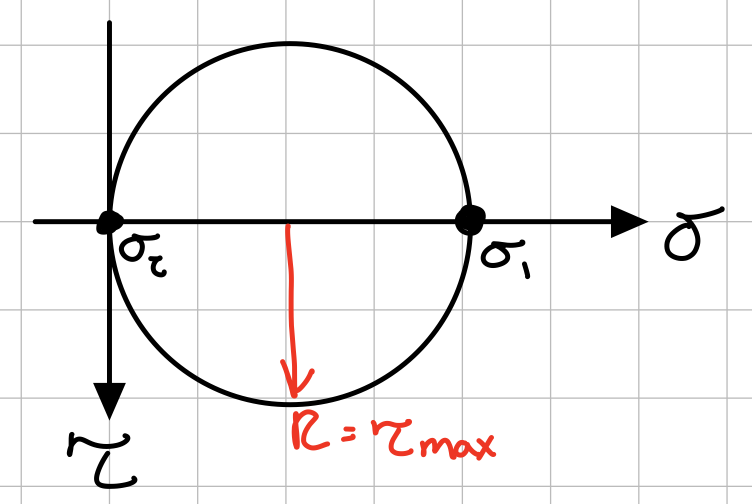
If a material is ductile, failure is defined by yield stress (\( \sigma_Y \)) and occurs at max shear stress (\( \tau_{max} \)).Uniaxial Tension
Tresca uniaxial tension.
Max shear.
General 2D Loading State
Plane stresses.
Tresca material failure.
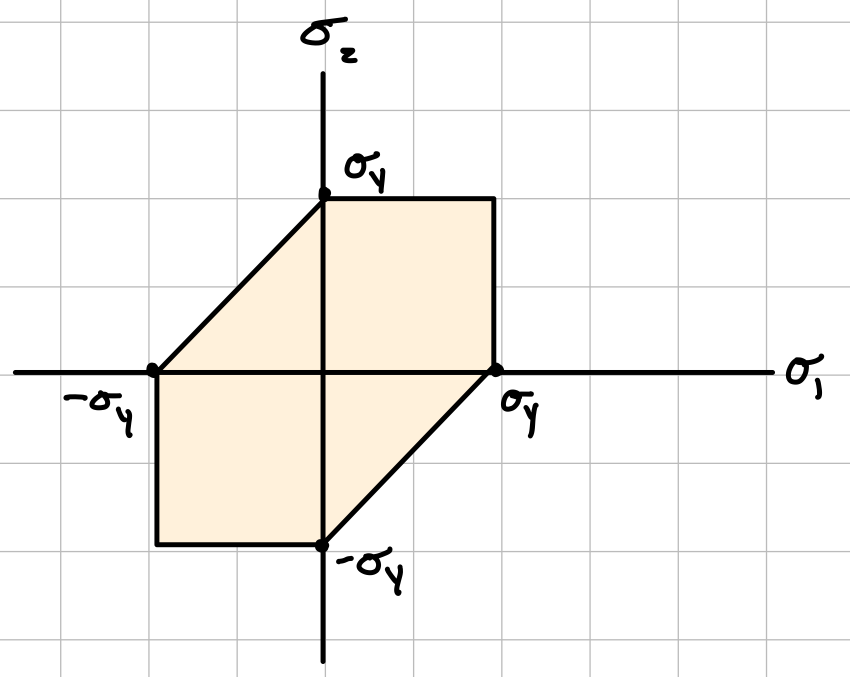
If \( \sigma_1 \) and \( \sigma_2 \) have the same signs:
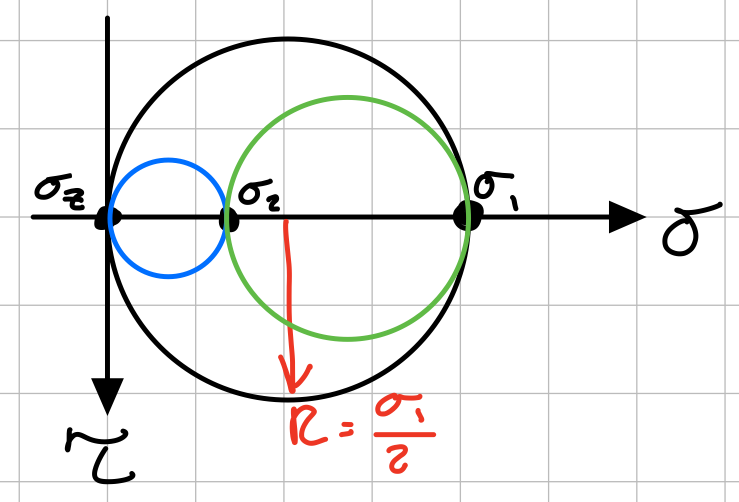
Tresca with same signs.
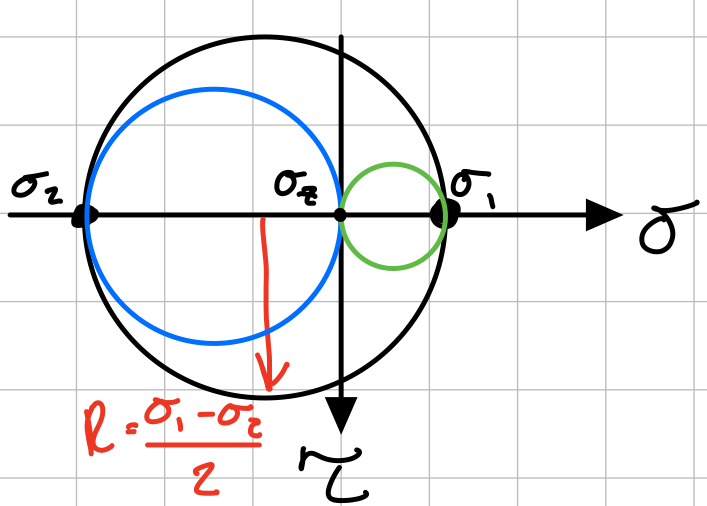
Tresca with opposite signs.
Maximum Distortion Energy (Von Mises) Criterion
Ductile materials likely do not fail due to stresses that only result in a volume change. It is hypothesized that failure is driven by distortion strain energy.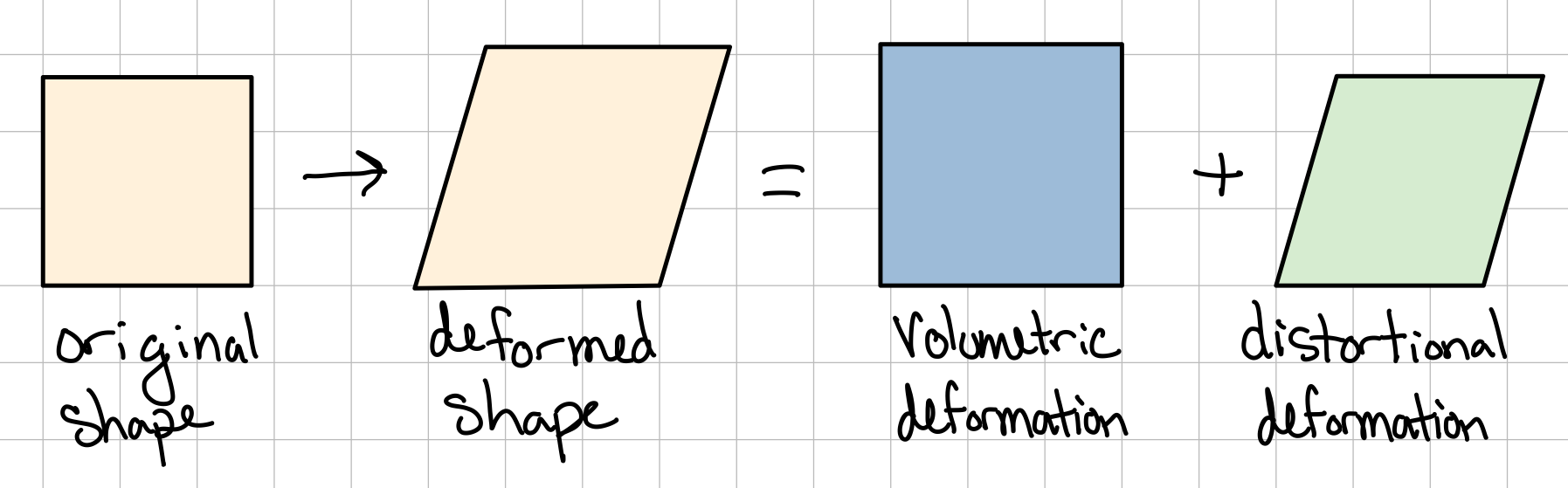
Von Mises material failure. #von-mis
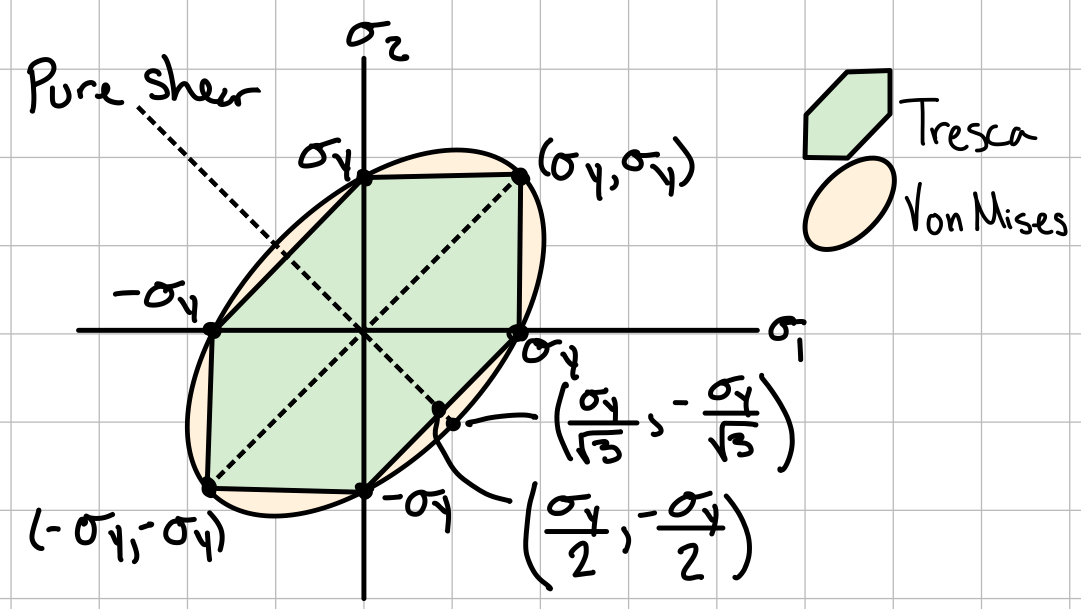
Interactive 3D Failure Surfaces
The following figure shows the failure surfaces of Tresca and von Mises criteria in term of the principal stresses in 3 dimensions. The 2D figure above can be found cenered around the origin in this plot. The shape of the 2D failure surface \( (\sigma_1,\sigma_2) \) remains the same, but moves location depending on \( \sigma_3 \). Just like in 2D, regions outside the surfaces are considered to have failed.
Loading...
Loading... Maximum Normal Stress Criterion
For brittle materials, failure is caused by the maximum tensile stress and NOT compressive stress. Maximum normal stress criterion material failure.