Buckling
Buckling is the sudden change in shape of a structural component under a compressive load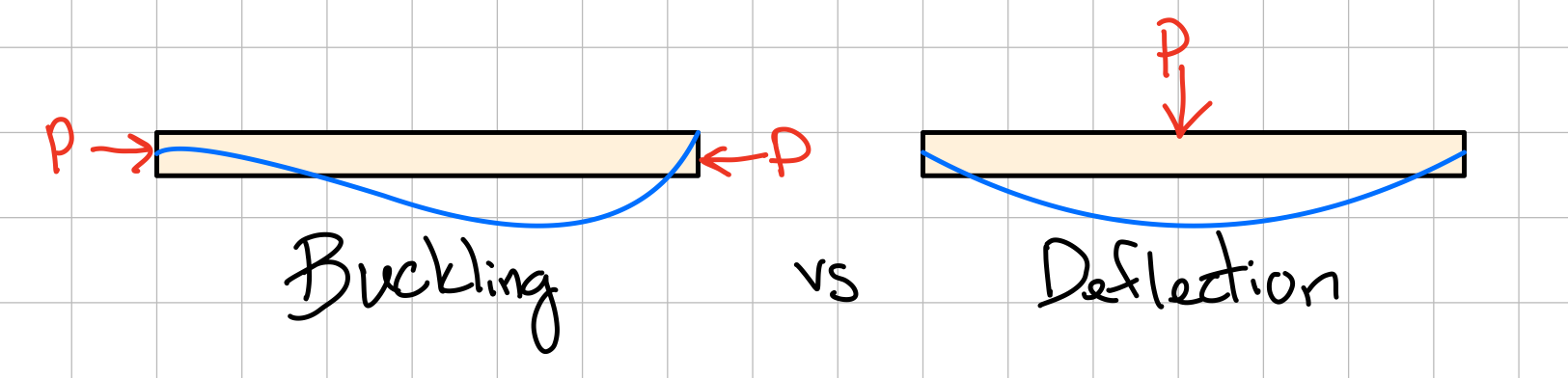
Single Column
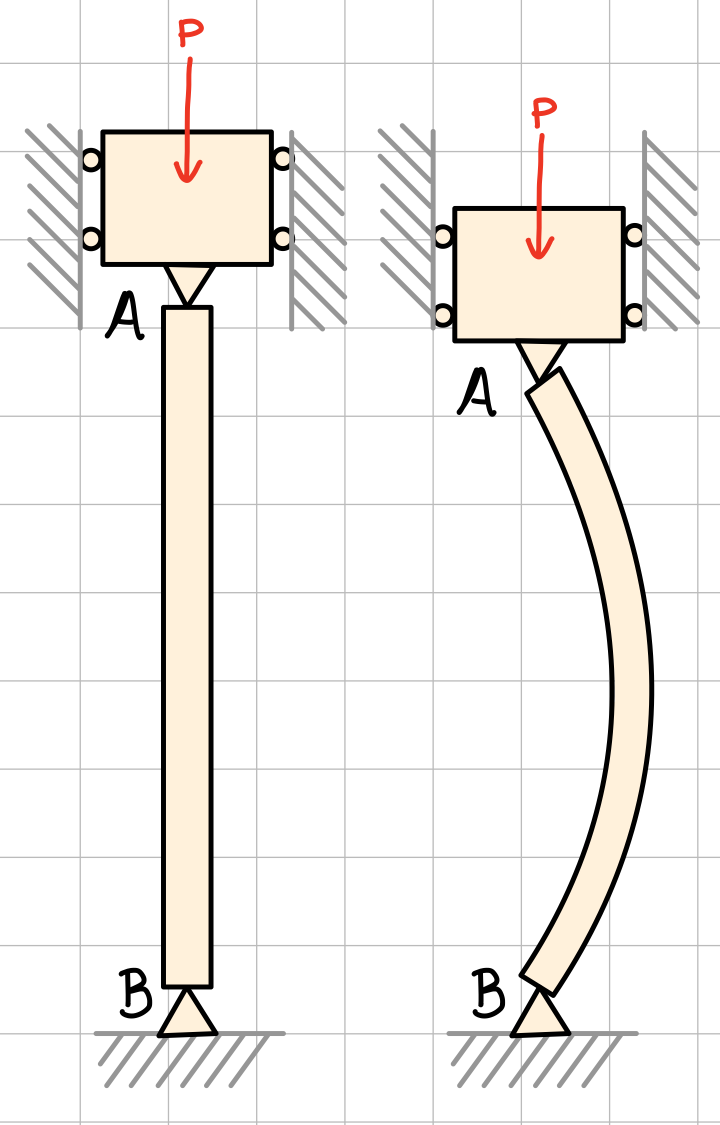
Uniaxial compressive load on single column.
Two Rods and a Torsional Spring
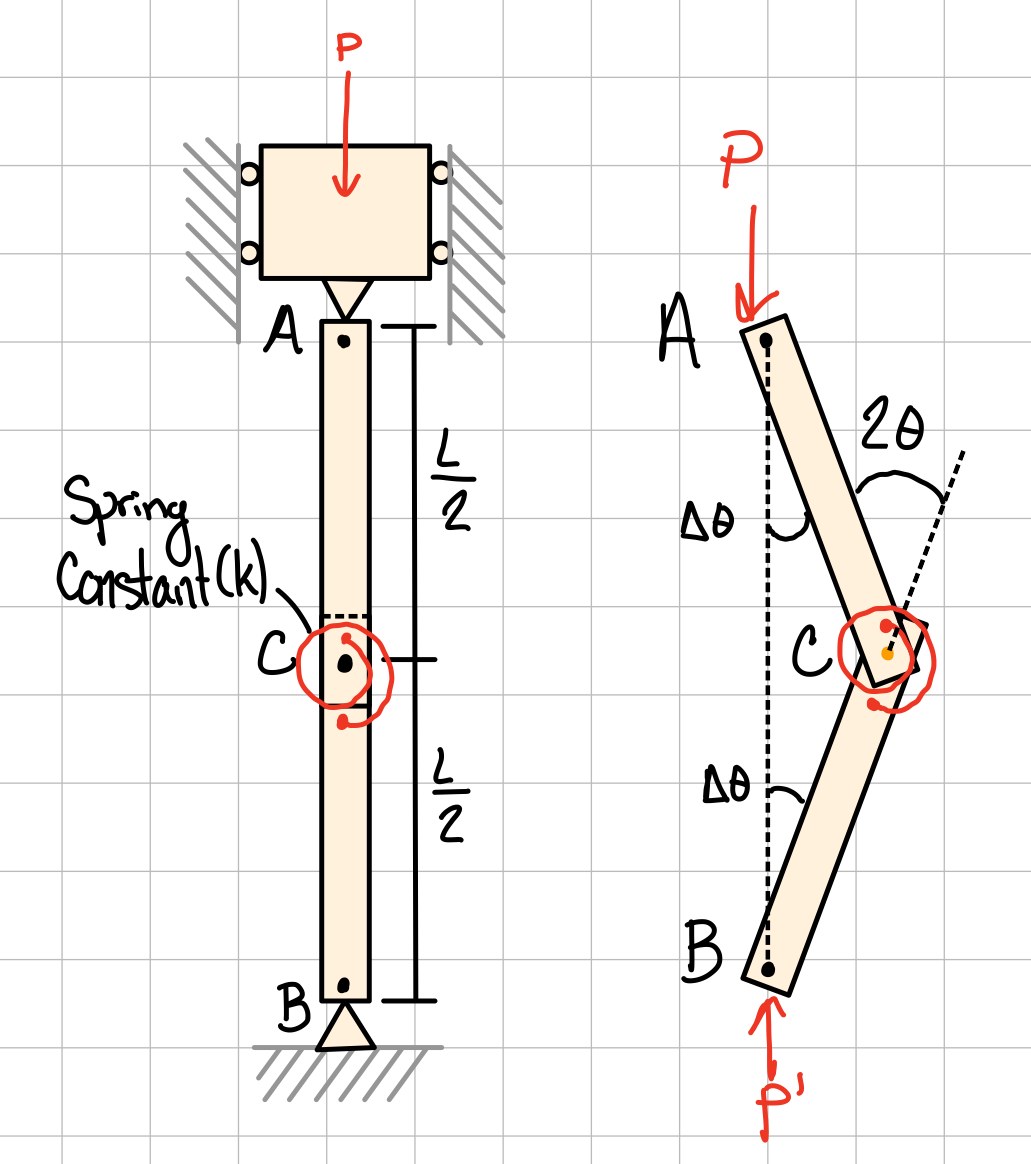
- If \( C \) returns to the original position, then the system is stable
- If \( C \) moves farther away from the original position, then the system is unstable
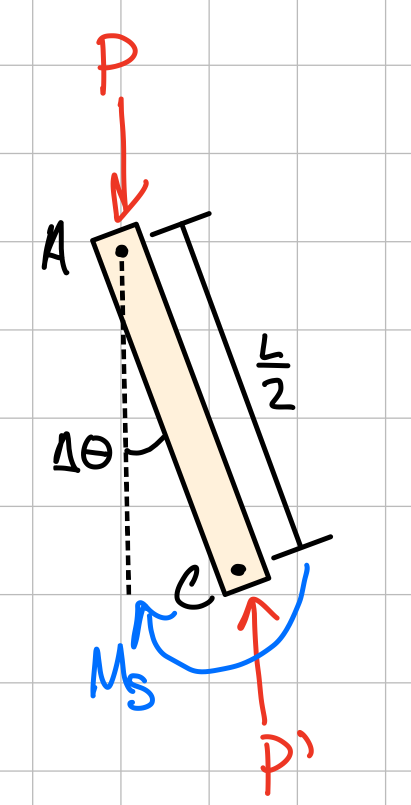
Spring restoring moment.
Sprind destabilizing moment.
- Stable system: \( M > M_{load} \)
- Unstable system: \( M< M_{load} \)
- Equilibrium position gives:\( M=M_{load} \)
Critical load. #crt-lod
Euler's Formula
Euler's formula can be used to solve for the critical load of a uniaxially loaded column.Pinned-end Columns
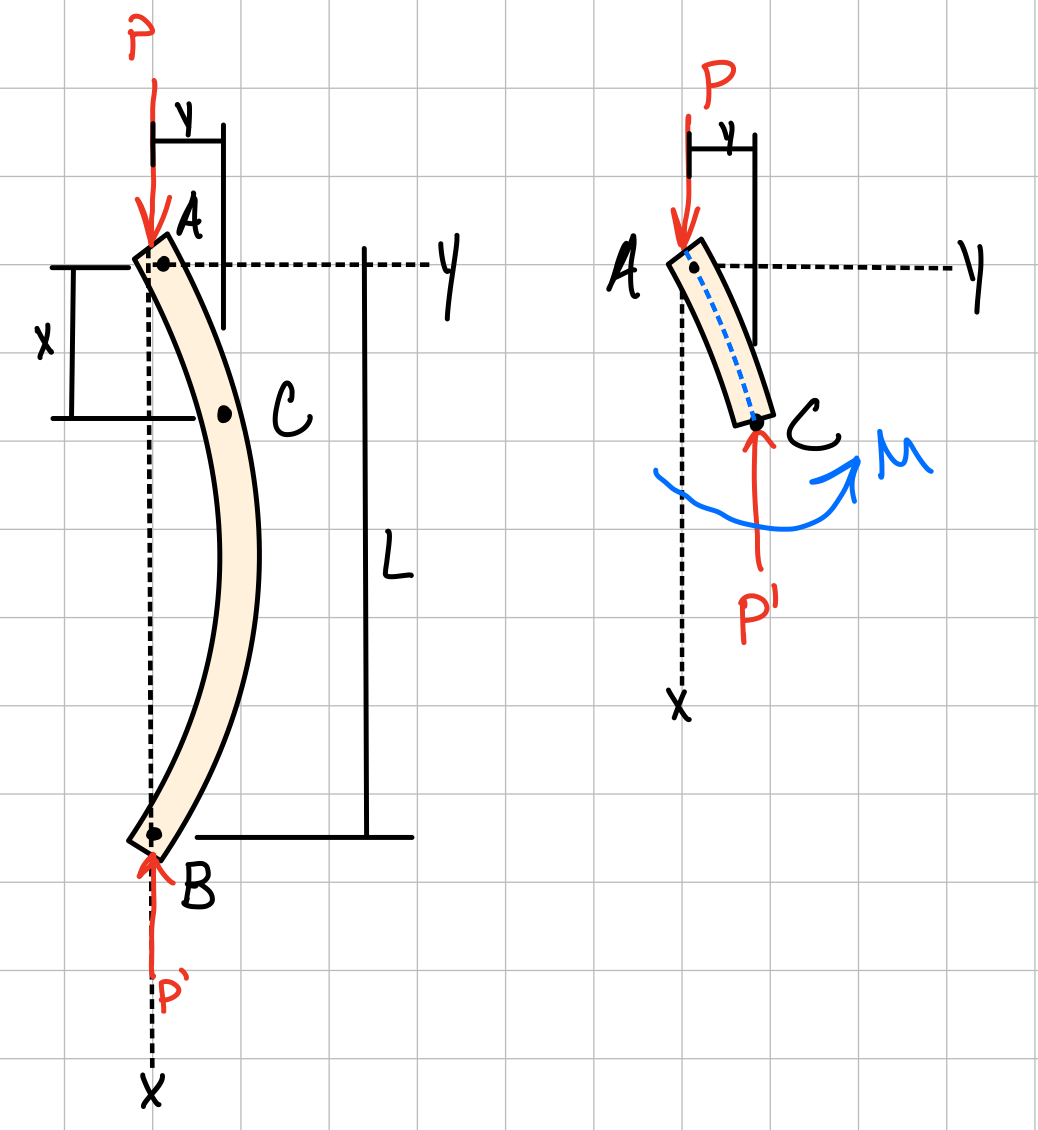
Pinned-end equilibrium. #pin-end
General solution.
Boundary conditions.
Euler's formula for buckling. #axl-fdr
Other Boundary Conditions
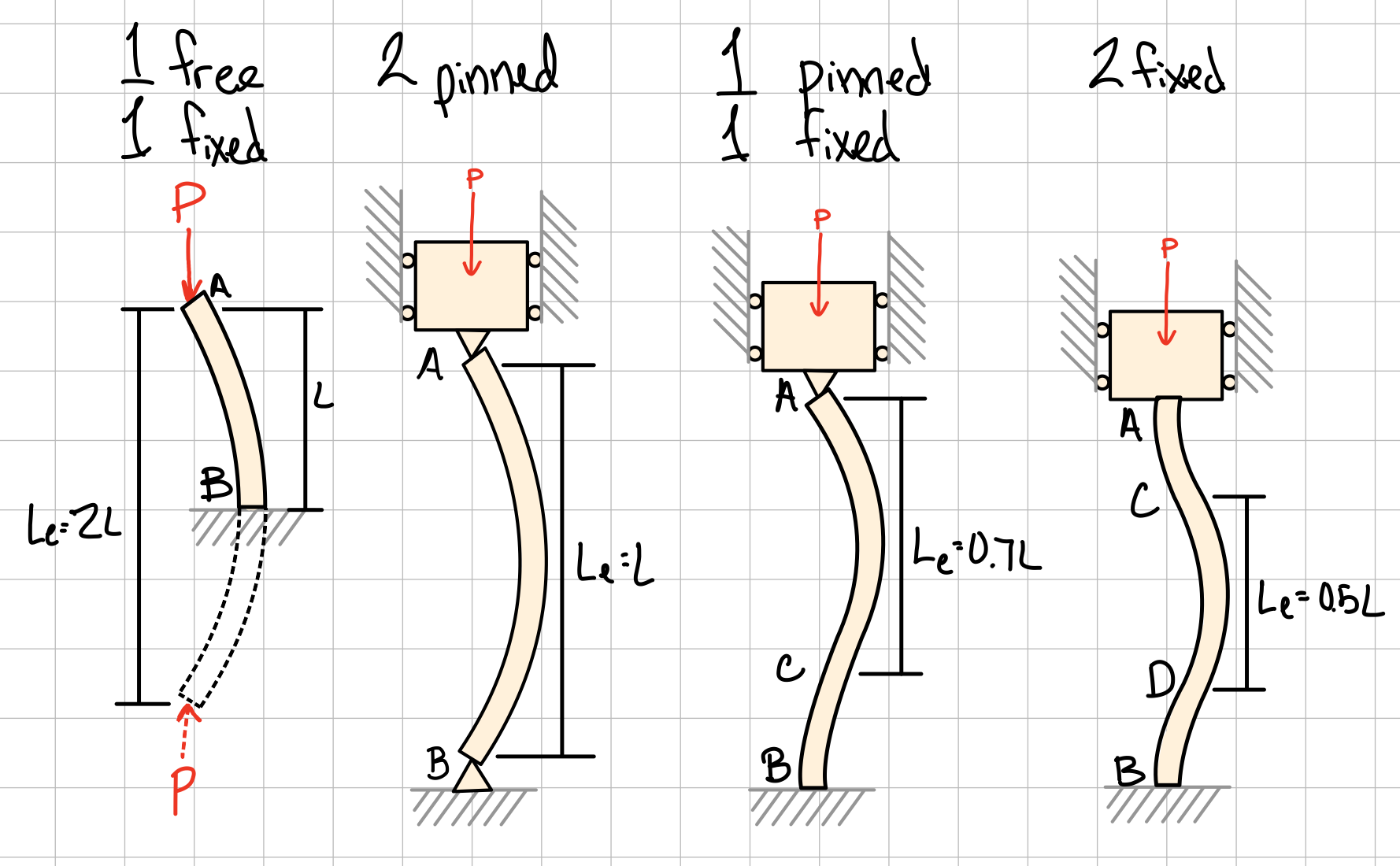
General critical load formula.