Beam Deflection
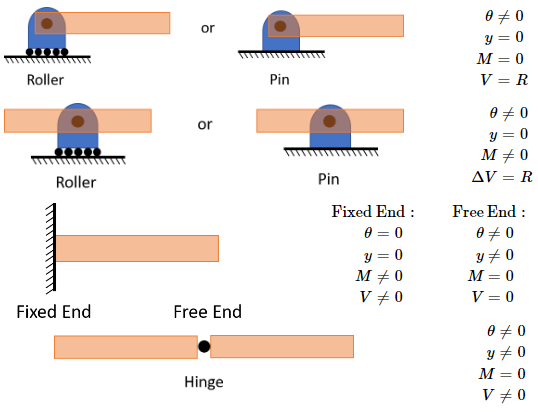
Goal: Determine the deflection and slope at specified points of beams and shafts.Solve statically indeterminate beams: where the number of reactions at the supports exceeds the number of equilibrium equations available.
Maximum deflection of the beam: Design specifications of a beam will generally include a maximum allowable value for its deflection.
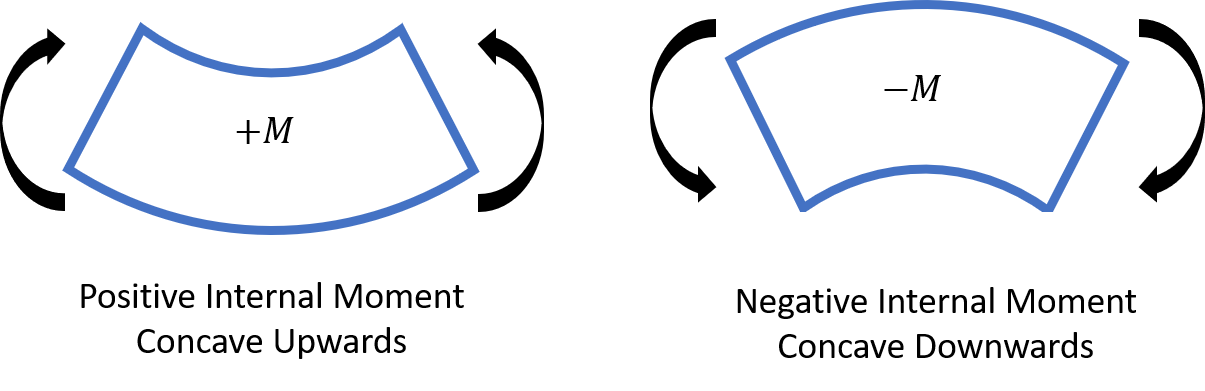
Moment-Curvature Equation
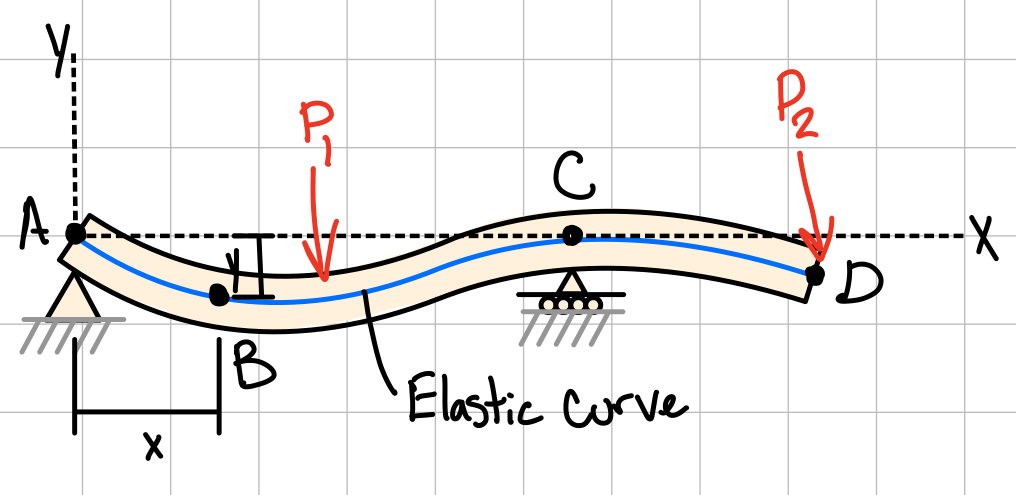
Moment-curve equation. #els-crv
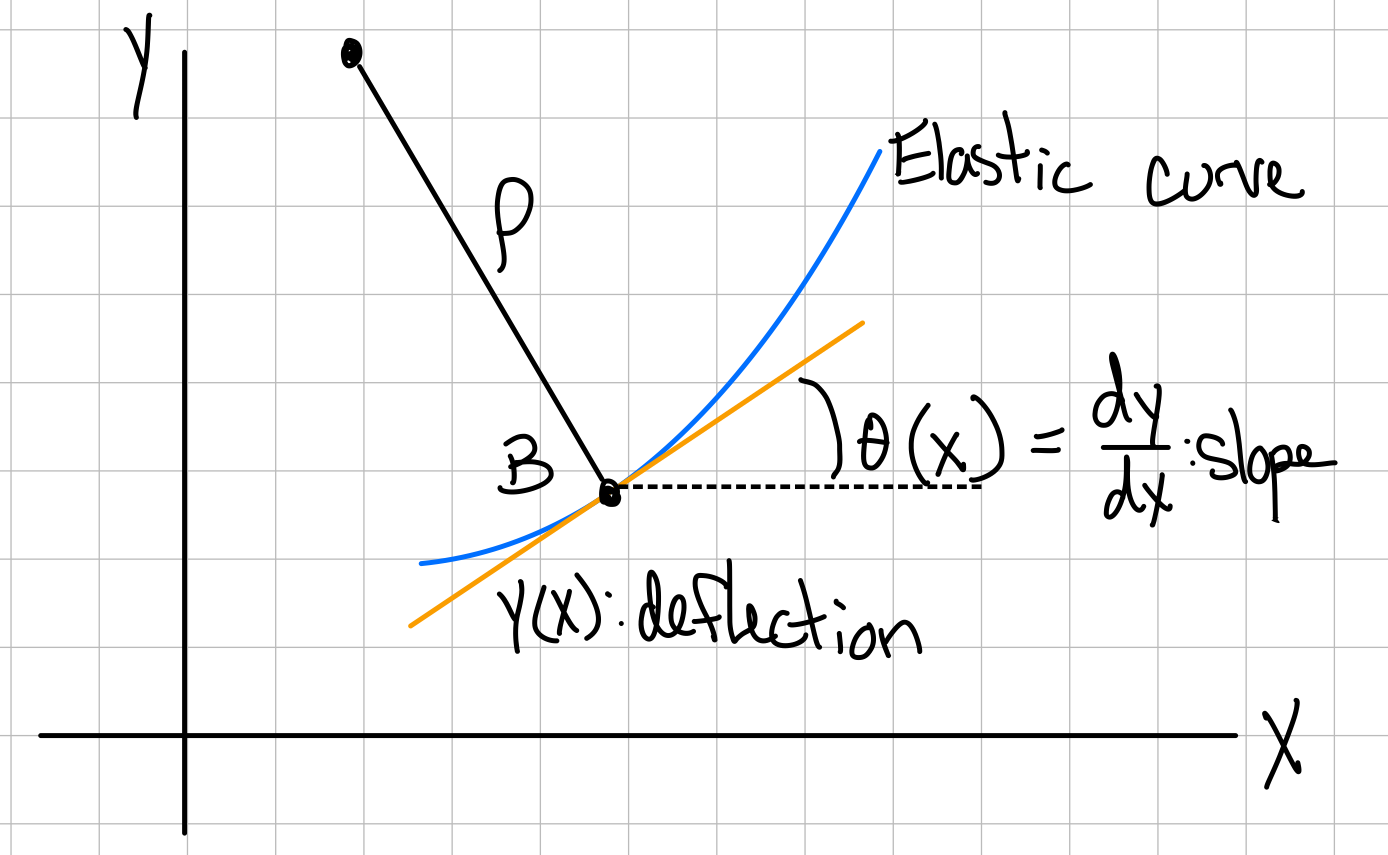
Elastic curve governing equation.
- Find the bending moment \( M(x) \).
- Integrate both sides of the governing equation twice.
- Solve for \( y(x) \).
Assumptions
- \( y(x) \) is the vertical direction
- Bending only: we will neglect effects of transverse shear
- Small deflection angles
Differentiation
Elastic curve equation for constant E and I.
Differentiating the elastic curve equation.
Differentiating the elastic curve equation a second time.
- \( EIy''(x): \) bending moment
- \( EIy '''(x): \) shear force
- \( EIy''''(x): \) distributed load
Integration
Shear force.
Internal bending moment.
Slope of the tangent line.
Deflection.
- \( y(x): \) deflection
- \( y'(x): \) slope
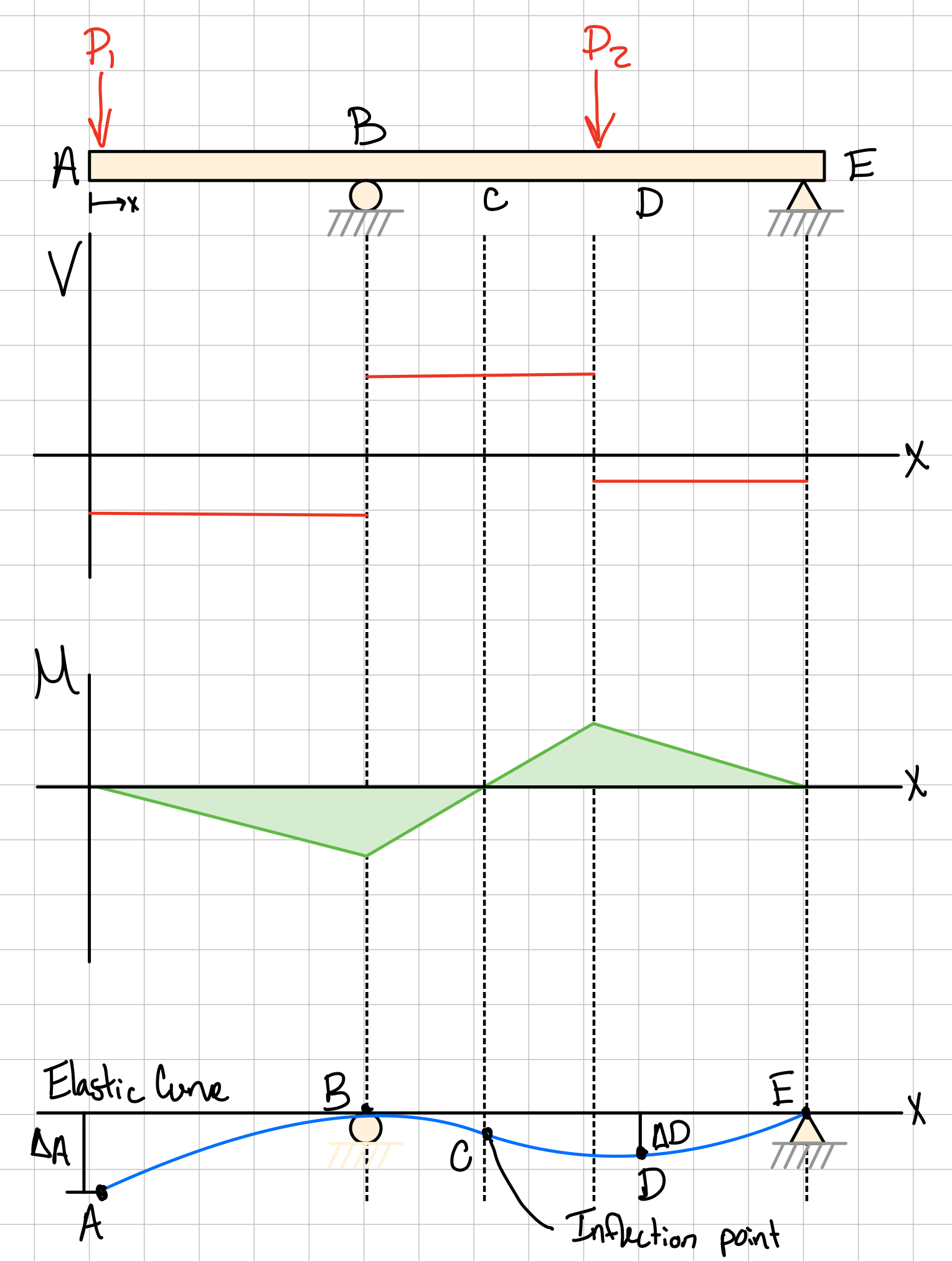
Example: Overhanging beam. #ovr-hng
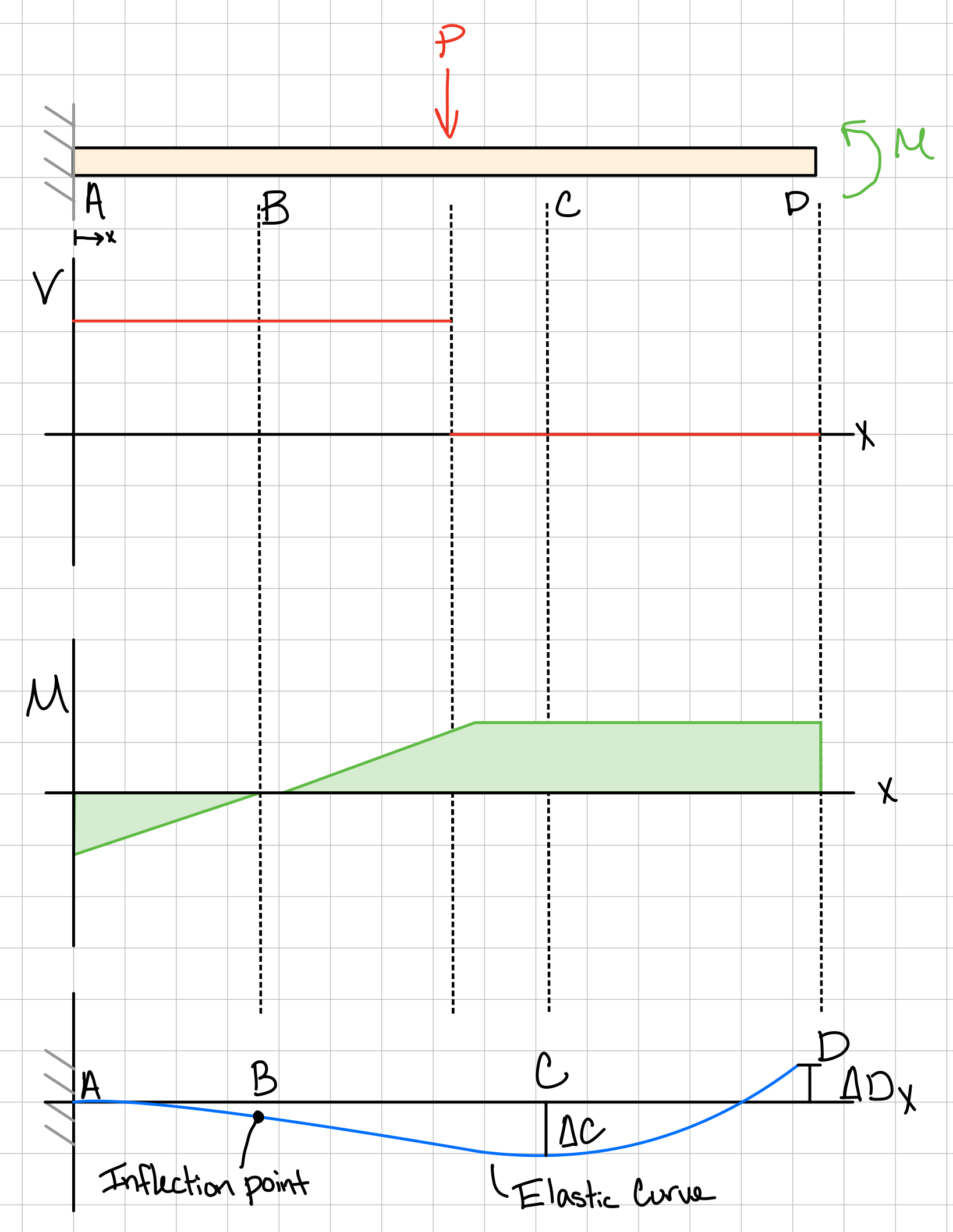
Example: Cantilever beam. #can-tlv
Beam Solutions
Common beam deflection solutions have been worked out.| Diagram | Max. deflection
\( y_{max} \) | Slope at end
\( \theta \) | Elastic curve
\( y(x) \) |
|---|---|---|---|
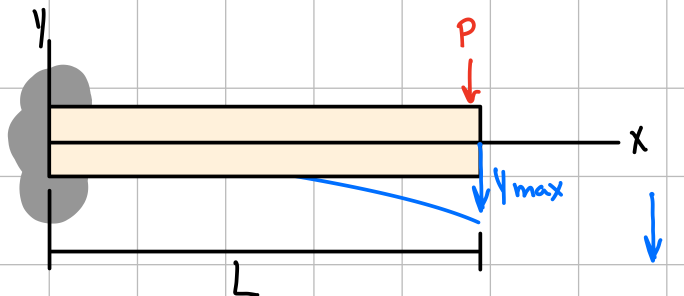 | \( -\frac{PL^3}{3EI} \) | \( -\frac{PL^2}{2EI} \) | \( \frac{P}{6EI}(x^3-3Lx^2) \) |
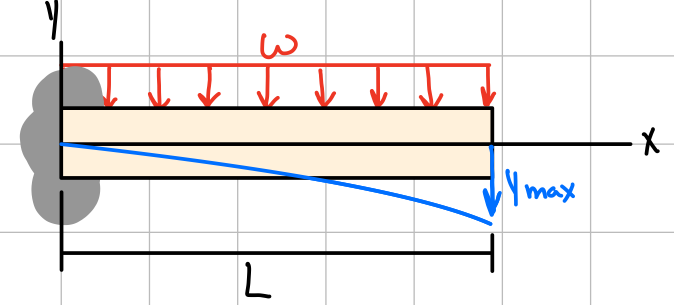 | \( -\frac{wL^4}{8EI} \) | \( -\frac{wL^3}{6EI} \) | \( -\frac{w}{24EI}(x^4-4Lx^3+6L^2x^2) \) |
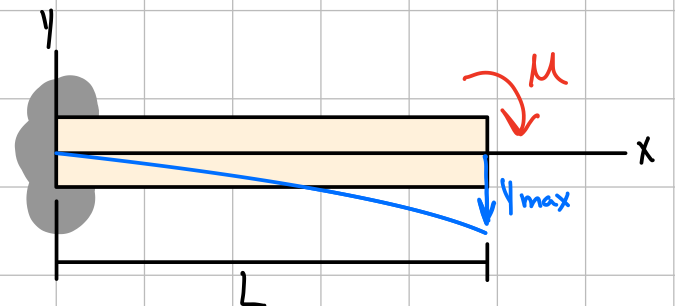 | \( -\frac{ML^2}{2EI} \) | \( -\frac{ML}{EI} \) | \( -\frac{M}{2EI}x^2 \) |
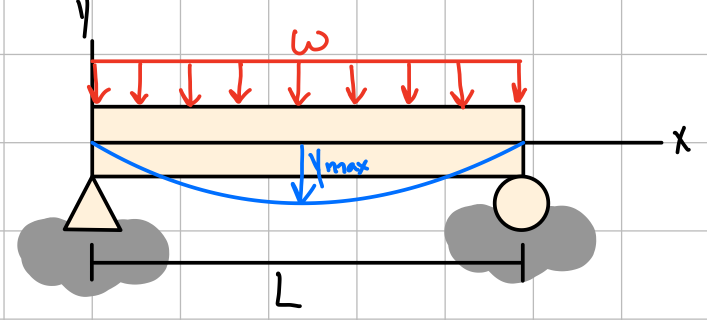 | \( -\frac{5wL^4}{384EI} \) | \( \pm\frac{wL^3}{24EI} \) | \( -\frac{w}{24EI}(x^4-2Lx^3+L^3x) \) |
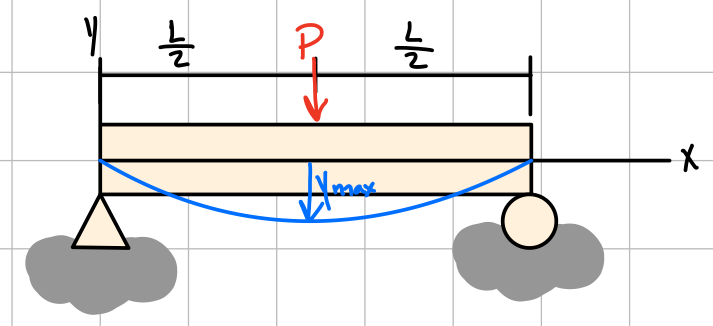 | \( -\frac{PL^3}{48EI} \) | \( \pm\frac{PL^2}{16EI} \) | For \( 0 \le x \le \frac{L}{2}: \) \( \frac{P}{48EI}(4x^3-3L^2x) \) |
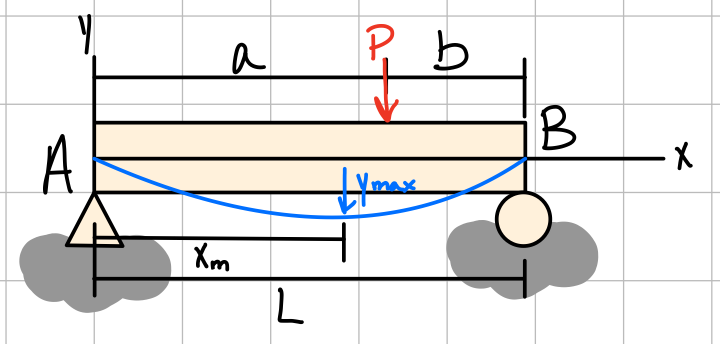 | For \( a>b: \) \( -\frac{Pb(L^2-b^2)^{\frac{3}{2}}}{9\sqrt{3}EIL} \)\( x_m = \sqrt{\frac{L^2-b^2}{3}} \) | \( B: -\frac{Pb(L^2-b^2)}{6EIL} \) \( A: +\frac{Pa(L^2-a^2)}{6EIL} \) | For \( x<a: \) \( \frac{Pb}{6EIL}(x^3-x(L^2-b^2)) \)For \( x=a: \) \( -\frac{Pa^2 b^2}{3EIL} \) |
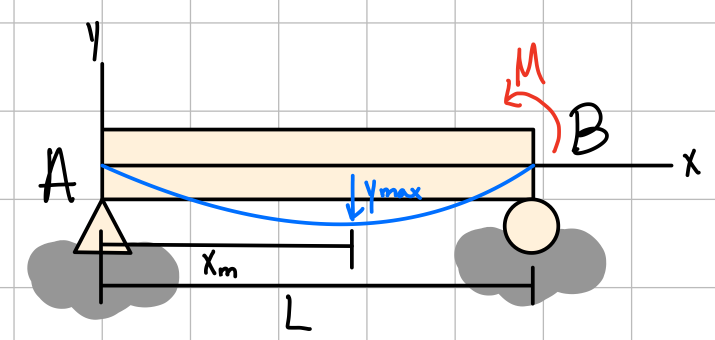 | \( -\frac{ML^2}{9\sqrt{3}EI} \) \( x_m = \frac{L}{\sqrt{3}} \) | \( A: -\frac{ML}{6EI} \) \( B: +\frac{ML}{3EI} \) | \( \frac{M}{6EIL}(x^3-L^2x) \) |
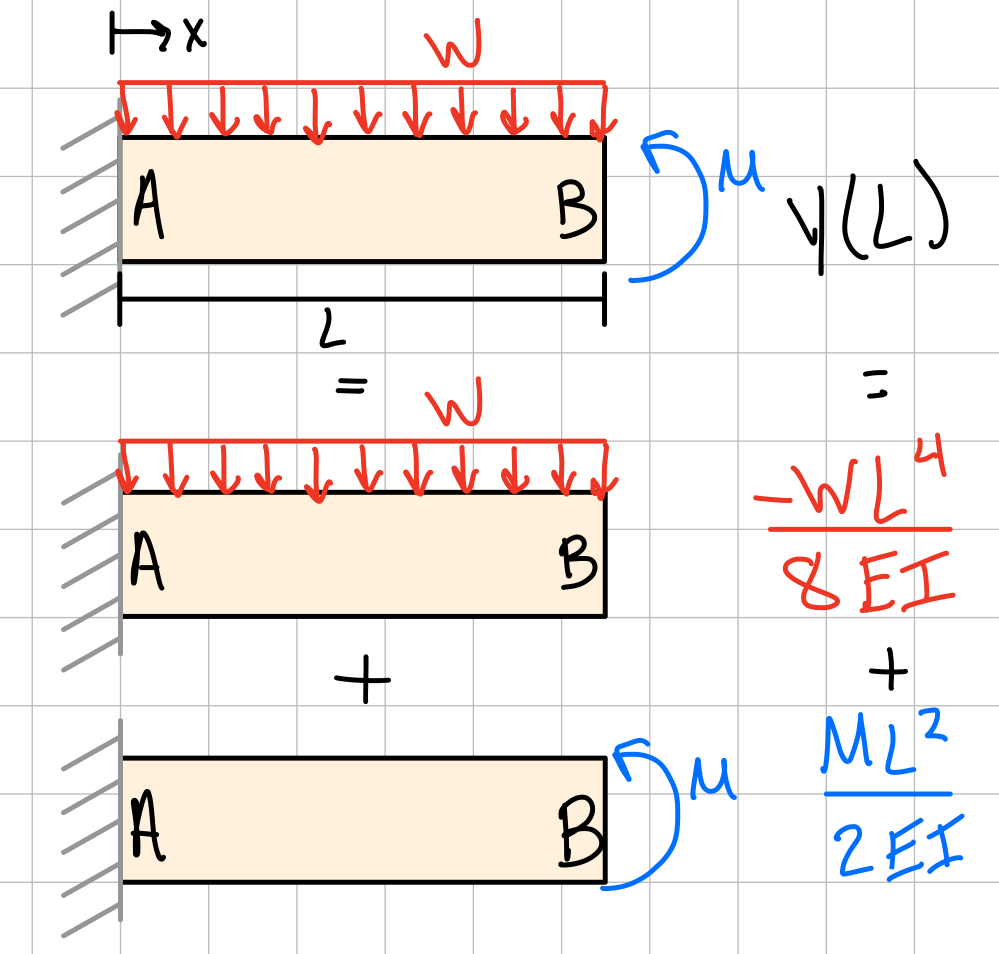
Example: Deflection from a moment and distributed load using superpositon. #dfl-spp