Rigid bodies

A rigid body is an extended area of material that includes all the points inside it, and which moves so that the distances and angles between all its points remain constant. The location of a rigid body can be described by the position of one point $P$ inside it, together with the rotation angle of the body (one angle in 2D, three angles in 3D).

	location description	velocity description
point mass	position vector $ \vec{r}_P $	velocity vector $ \vec{v}_P $
rigid body in 2D	position vector $ \vec{r}_P $ angle $\theta$	velocity vector $ \vec{v}_P $ angular velocity $ \omega $
rigid body in 3D	position vector $ \vec{r}_P $ angles $ \theta,\phi,\psi $	velocity vector $ \vec{v}_P $ angular velocity vector $ \vec{\omega} $

Neither point masses nor rigid bodies can physically exist, as no body can really be a single point with no extent, and no extended body can be exactly rigid. Despite this, these are very useful models for mechanics and dynamics.

Rotating rigid bodies

All points on a rigid body have the same angular rotation angles, as we can see on the figure below. Because the angular velocity is the derivative of the rotation angles, this means that every point on a rigid body has the same angular velocity $ \vec{\omega} $, and also the same angular acceleration $ \vec{\alpha} $.

In 2D the angle $ \theta $ of a rigid body the angle of rotation from a fixed reference (typically the $ \hat\imath $ direction), measured positive counter-clockwise. The angular velocity is $ \omega = \dot\theta $ and the angular acceleration is $ \alpha = \dot\omega = \ddot\theta $. The vector versions of these are $ \vec\omega = \omega \, \hat{k} $ and $ \vec\alpha = \alpha\,\hat{k} $, where $ \hat{k} $ is the out-of-plane direction.

Show:

All points on a rigid body rotate at the same rate. Body $ \mathcal{B}_1 $ is rotated by angle $\theta_1$, so its angular velocity is $ \omega_1 = \dot{\theta}_1 $, and similarly for the second body.

Warning: Labeling angular quantities on rigid bodies. #rkg-ww

Angular quantities ($ \theta , \omega , \alpha $)for rigid bodies should not be labeled with points. If P and Q are points on a rigid body, we do not write $ \omega_P $ or $ \omega_Q $ for the angular velocity about these points.

Instead, we label angular quantities according to the body. If we have two rigid bodies $ B_1 $ and $ B_2 $, then $ \omega_1 $ is the angular velocity of the first body (and all points on it) and $ \omega_2 $ is the angular velocity of the second body.

Did you know?

Rotations in 3D are significantly more complicated than rotations in 2D. Unlike positions, velocities, etc, which simply go from 2D vectors to 3D vectors, rotational quantities go from scalars in 2D to full 3D vectors in 3D. Angular velocity and angular acceleration are somewhat straightforward, so equations #rkg-er hold in both 2D and 3D, but understanding the rotations themselves is significantly more complicated. There are three main ways that 3D rotations can be represented:

Detailed study of rotations in 3D is necessary for a full understanding of topics ranging from satellite attitude control to articulated robot construction, and is usually covered in advanced dynamics courses.

Points on rigid bodies

If we know how one point $P$ on a rigid body is moving and we also know how the body is rotating, then we can calculate the movement of any other point $Q$ on the same body. The formulas for this are given below.

Rigid body point relations. #rkg-er

$$ \begin{aligned}\vec{r}_Q &= \vec{r}_P + \vec{r}_{PQ} \\\vec{v}_Q &= \vec{v}_P+ \vec{\omega} \times \vec{r}_{PQ} \\\vec{a}_Q &= \vec{a}_P+ \vec{\alpha} \times \vec{r}_{PQ}+ \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ})\end{aligned} $$

Points $P$ and $Q$ are two locations on a rigid body. Vectors $ \vec{\omega} $ and $ \vec{\alpha} $ are the angular velocity and angular acceleration of the rigid body.

The first equation is simply the definition of the offset vector $ \vec{r}_{PQ} $. Differentiating the first equation gives

$$ \begin{aligned} \vec{r}_Q &= \vec{r}_P + \vec{r}_{PQ} \\ \dot{\vec{r}}_Q &= \dot{\vec{r}}_P + \dot{\vec{r}}_{PQ} \\ \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ}, \end{aligned} $$

where the derivative of $ \vec{r}_{PQ} $ comes from the rotation formula, given that this offset vector is simply rotating with the rigid body.

If we differentiate again then we obtain

$$ \begin{aligned} \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ} \\ \dot{\vec{v}}_Q &= \dot{\vec{v}}_P + \dot{\vec{\omega}} \times \vec{r}_{PQ} + \vec{\omega} \times \dot{\vec{r}}_{PQ} \\ \vec{a}_Q &= \vec{a}_P + \vec{\alpha} \times \vec{r}_{PQ} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}), \end{aligned} $$

where we use the fact that $ \vec{\alpha} = \dot{\vec{\omega}} $.

Warning: Cross product order #rkg-wc

Because cross products are not associative, it is very important to compute the centripetal acceleration term with the parentheses as shown. That is, we must not compute $ (\vec{\omega} \times \vec{\omega}) \times \vec{r}_{PQ} $, as this is always zero.

The term $ \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}) $ in the acceleration equation above is called the centripetal (center-seeking) term, as it is always in the direction $ -\vec{r}_{PQ} $ and so acts from $Q$ towards the “center” $P$.

Show: none position velocity acceleration

Two points $P$ and $Q$ on a moving and accelerating rigid body.

Example Problem: Points on a rigid body #rkg-xp

A rectangular block is sliding along the ground so that the contact point $P$ is moving at a constant speed of $3\rm\ m/s$ to the left. The block is rotating clockwise and just before point $Q$ hits the ground the angular velocity is $2\rm\ rad/s$ clockwise and the angular acceleration is $3\rm\ rad/s^2$ clockwise. What is the velocity and acceleration of $Q$ just before impact?

Using the regular $ \hat\imath,\hat\jmath $ basis, the known information just before impact is

$$ \vec{r}_{PQ} = 2\,\hat\imath \qquad \vec{v}_P = -3\,\hat\imath \qquad \vec{a}_P = 0 \qquad \vec\omega = -2\,\hat{k} \qquad \vec\alpha = -3\,\hat{k}. $$

The velocity and acceleration of $Q$ are given by

$$ \begin{aligned} \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ} \\ &= -3\,\hat\imath - 2\,\hat{k} \times 2\,\hat\imath \\ &= -3\,\hat\imath - 4\,\hat\jmath \\ \vec{a}_Q &= \vec{a}_P + \vec{\alpha} \times \vec{r}_{PQ} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}) \\ &= 0 - 3\,\hat{k} \times 2\,\hat\imath - 2\,\hat{k} \times (-2\,\hat{k} \times 2\,\hat\imath) \\ &= -6\,\hat\jmath - 2\,\hat{k} \times (-4\,\hat\jmath) \\ &= -8\,\hat\imath - 6\,\hat\jmath. \end{aligned} $$

Example Problem: Coupled rigid bodies #rkg-xc

Three rigid bodies (two rods and a block) are coupled by pins at $O$, $P$, and $Q$ as shown. Body $ \mathcal{B}_3 $ cannot rotate and must slide horizontally along the ground. The rod lengths are $ OP = 3\sqrt{2}\rm\ m $ and $ PQ = 5\rm\ m $, and points $O$ and $Q$ are the same height above the ground.

At the instant shown, $ \theta_1 = 45^\circ $, $ \omega_1 = 4\rm\ rad/s $ . What are $ \omega_2 $ and $ \vec{v}_Q $ at this instant?

Taking a regular $ \hat\imath,\hat\jmath $ basis at $O$, we can use the rod lengths and angles to find the relative position vectors:

$$ \begin{aligned} \vec{r}_{OP} &= 3\hat\imath + 3\hat\jmath\rm\ m \\ \vec{r}_{PQ} &= 4\hat\imath - 3\hat\jmath\rm\ m. \end{aligned} $$

Using the vector angular velocities $ \vec{\omega}_1 = \omega_1\,\hat{k} $ and $ \vec{\omega}_2 = \omega_2\,\hat{k} $, we can now use #rkg-er to find first $ \vec{v}_P $ and then $ \vec{v}_Q $ in terms of the unknown angular velocity $\omega_2$:

$$ \begin{aligned} \vec{v}_{P} &= \vec{v}_O + \vec{\omega}_1 \times \vec{r}_{OP} \\ &= 4\hat{k} \times (3\hat\imath + 3\hat\jmath) \\ &= -12\hat\imath + 12\hat\jmath{\rm\ m/s} \\ \vec{v}_{Q} &= \vec{v}_P + \vec{\omega}_2 \times \vec{r}_{PQ} \\ &= (-12\hat\imath + 12\hat\jmath{\rm\ m/s}) + \omega_2\,\hat{k} \times (4\hat\imath - 3\hat\jmath) \\ &= (-12 + 3\omega_2)\,\hat\imath + (12 + 4\omega_2)\,\hat\jmath{\rm\ m/s}. \end{aligned} $$

The last piece of information that we need to use is the constraint on the motion of $ \mathcal{B}_3 $, namely that it can only slide horizontally. This can be expressed by saying that the vertical component of $ \vec{v}_Q $ is zero, or more generally that the component in the normal direction $ \hat{e}_n = \hat\jmath $ is zero. That is:

$$ \begin{aligned} 0 &= \vec{v}_Q \cdot \hat{e}_n \\ &= \Big((-12 + 3\omega_2)\,\hat\imath + (12 + 4\omega_2)\,\hat\jmath\Big) \cdot \hat\jmath \\ &= 12 + 4\omega_2 \\ \omega_2 &= -3{\rm\ rad/s}. \end{aligned} $$

Substituting this back into the expression above for $ \vec{v}_Q $ gives:

$$ \vec{v}_Q = -21\hat\imath{\rm\ m/s}, $$

which does indeed have no vertical component, as expected.

Warning: Rigid body points may be accelerating even if $\vec{a}_P = 0$ and $\alpha = 0$. #rkg-wa

If $ \vec{\alpha} = 0 $ and $ \vec{a}_P = 0 $ for a rigid body then we would normally say that the body itself is not accelerating. This does not mean, however, that the points on the bodies are not accelerating. If the body is rotating (so $ \vec{\omega} \ne 0 $) then the centripetal acceleration means that in fact most points on the body are accelerating at any time.

Constrained motion

One of the most common type of motion is constrained motion, where an object is restricted to move in a certain way.

Generally, a point constrained to move in a specific direction obeys the following equation:

Constraint equation for a point $P$. #rkc-pc

$$ \vec{v}_P \cdot \hat{n}_P = 0 $$

where $ \hat{n}_P $ is the normal vector to the motion of point $P$.

The above equation is difficult to apply to a system with a collection of points or particles. It is not the only way to derive constraint equations. For example, rigid body kinematics equations (also known as relative motion equations) are derived using the definition of a rigid body. Namely, the distance and angles between all points remain constant. See rigid body relations. It is often best to look at examples of constrained motion to see how constraint equations are differentiated to obtain velocity and acceleration.

We can visualize the motion of several constrained systems, shown on the figure below.

System:

rod-circular

slider-crank

rod-circular

slider-crank

Example Problem: Sliding rod #rkc-xcl

A uniform rod leaning against a wall has a fixed length of $\ell = 10 \rm\ m$. The bottom of the rod at point $P$ is $8 \rm\ m$ from the wall. Point $P$ is moving away from the wall at a speed of $6 \rm\ m/s$. The rod maintains contact with the wall and ground at all times. What is $ \vec{v}_Q $ of point $Q$, the point at the top of the rod?

To solve this, note the question states that the rod's length is fixed, and is not permitted to lose contact with the wall and ground. Therefore, the constraint equation is given by the Pythagorean theorem:

$$ \begin{aligned} x_P^2 + y_Q^2 = \ell^2 \end{aligned} $$

This becomes a related rates problem from calculus 1.

Differentiating with respect to time, keeping in mind the chain rule:

$$ \begin{aligned} 2x_P\dot{x}_P + 2y_Q\dot{y}_Q = 0 \end{aligned} $$

The quantity we're interested in is $ \dot{y}_Q $ , or $ v_Q $, and $ y_Q = \sqrt{\ell^2 - x_P^2} $ .

Solving yields $ \vec{v}_Q = -8\hat{\jmath} \rm\ m/s $ .

Another way to solve this is using the rigid body relations, knowing that the distance and angles from the top to the bottom of the rod remains constant, which is a rigid body by definition. Using rigid body relations:

$$ \begin{aligned} \vec{v}_Q &= \vec{v}_P + \vec\omega \times \vec{r}_{PQ} \\ &= \vec{v}_P + \omega_z \vec{r}_{PQ}^{\perp} \end{aligned} $$

where we have two unknowns:$ \vec{v}_Q $ , and $\vec\omega$, and $ \vec{r}_{PQ} = -\ell \cos\theta \hat{\imath} + \ell \sin\theta \hat{\jmath} \rm\ m $, where $ \theta = \cos^{-1}\left(\frac{x_P}{\ell}\right) $.

Therefore, $ \vec{r}_{PQ}^{\perp} = -\ell \sin\theta \hat{\imath} - \ell \cos\theta \hat{\jmath} \rm\ m $ .

Expanding the vector equation into its two scalar equations yields:

$$ \begin{aligned} v_{Qx} &= v_{Px} - \omega_z \ell \sin\theta \\ v_{Qy} &= v_{Py} - \omega_z \ell \cos\theta \end{aligned} $$

Since the top of the rod can only move vertically, $ v_{Qx} = 0, and \omega_z = \frac{v_{Px}}{\ell \sin\theta} \rm\ rad/s $

Since the bottom of the rod can only move horizontally, $ v_{Py} = 0, and v_{Qy} = -\omega_z \ell \cos\theta \rm\ m/s $

Plugging in $\omega_z$ expression:

$$ v_{Qy} = -\frac{v_{Px}}{\ell \sin\theta} \ell \cos\theta = -v_{Px}\cot\theta \rm\ m/s $$

Plugging in the numbers yields the same result of $ \vec{v}_{Q} = -8\hat{\jmath} \rm\ m/s $ .

Note in the rigid body relations method, we implicitly used the constraint equation for a point. Namely, we know that the top of the rod can only move vertically, so $ \vec{v}_Q \cdot \hat{n}_Q = 0 $ , where $ \hat{n}_Q = \hat{\imath} $ and $ \vec{v}_P \cdot \hat{n}_P = 0 $ , where $ \hat{n}_P = \hat{\jmath} $.

In general, the steps involved in analyzing systems with constrained motions are as follows:

Solution procedure for constrained motion. #rkc-cp

$$ \begin{aligned}&\text{1. Write down constraint equation in terms of distances/positions.} \\&\text{2. Differentiate once or twice with respect to time to obtain} \\& \quad \vec{v} \quad \text{and} \ \vec{a} \ \text{relationships.} \\&\text{3. Solve for the desired quantity.}\end{aligned} $$

Example Problem: Compound pulley system #rkc-xcp

Consider the compound pulley system shown, consisting of two massless pulleys $A, B$. Pulley $A$ is free to move vertically, and pulley $B$ is fixed to the top. The two pulleys are connected by an inextensible, massless rope. One block of mass $m_1$ is connected to pulley $A$ by a string, and another block of mass $m_2$ is hanging from the rope connecting the two pulleys. Assume the pulleys' radii are negligbile. If $m_2$ moves downwards at a velocity $v_2 = 6 \rm\ m/s$ and acceleration $a_2 = 2 \rm\ m/s^2$, what are the velocity and acceleration of $m_1$?

We will begin by underlining important information given in the question. Namely:

The rope is inextensible, meaning the total length of the rope remains constant. This is our constraint.
The pulleys are massless, meaning we do not need to consider any rotational motion they may exhibit.
The pulleys radii' are negligbile, meaning we do not need to consider their radii as a part of the total length of the rope.

Using the solution procedure highlighted in #rkc-cp:

1. Write down constraint equation in terms of distances/positions. If the rope's length remains constant, we need to choose a reference line to relate the distances of the masses to that reference line and set it equal to the rope's length. The following figure shows the reference line, as well as the masses' distances from that line.

Note that $y_1$ is only extended to pulley $A$. Since the pulleys are massless, they will not rotate, and therefore $m_1$ and pulley $A$ will translate vertically together at the same rate.

Now, we can write the total length of the rope in terms of those two distances. The total length of the rope,$L$ will be:

$$ 2y_1 + y_2 = L $$

2. Differentiate once or twice with respect to time to obtain $ \vec{v} $ and $ \vec{a} $ relationships. Now, we can take two derivatives with respect to time to obtain the relationship between the speeds $ v_1, v_2 $ , and the accelerations $ a_1, a_2 $ .

$$ \begin{aligned} 2v_1 + v_2 &= 0 \\ 2a_1 + a_2 &= 0 \end{aligned} $$

Notice that the length of the rope does not matter ultimately. This makes sense, as the length of the rope is constant, and therefore does not change with time.

3. Solve for the desired quantity. We are interested in both the velocity and acceleration of $m_1$.
Solving for $ \vec{v}_1 = \frac{-\vec{v}_2}{2} = 3\hat{\jmath}\rm\ m/s $ and $ \vec{a}_1 = \frac{-\vec{a}_2}{2} = \hat{\jmath}\rm\ m/s^2 $

Reflecting on the result obtained, it makes sense. The distance $m_1$ has to travel up the rope is two times more than the length $m_2$ has to travel. We can also draw a free-body diagram to understand this result further. We will return to this example further down when constraint forces are covered.

Reference material

Calculus and vectors
Rigid bodies
Kinetics of point masses
Kinetics of rigid bodies
Free body diagrams
Energy and work

Applications

Four-bar linkages

Constraint forces

If an object is constrained to move in a specific direction, by Newton's second law, there must be forces or moments preventing the movement of the object in that direction. Those are called constraint forces.

The approach to solving for constraint forces is the same approach to solve for any forces/moments that are not constraint forces. Namely, drawing a free body diagram, and applying Newton's equations. See the solution procedure with Newton's equations.

Let's return to our example of the rod leaning against a wall.

Example Problem: Constraint forces on a sliding rod. #rkc-xcf

A uniform rod of mass $m$ and length $\ell$ is leaning against a frictionless wall at an angle $\phi$ as shown. The rod starts sliding along a frictionless ground under the influence of gravity $ \vec{g} $. What are the expressions of the constraint forces $ \vec{F}_P, \vec{F}_Q $ that ensure the rod maintains contact with the wall and ground at all times?

We will begin by drawing a free body diagram on the rod.

Note that due to the constraint placed on the rod, point $P$ can only slide along the ground and therefore by #rkc-pc, $ \vec{F}_P $ acts vertically. Similarly for point $Q$, $ \vec{F}_Q $ acts horizontally.

Applying Newton's second law:

$$ \sum \vec{F}_{ext} = m\vec{a}_C $$

Breaking it up into the scalar equations. Note we will use $ \ddot{x}_C, \ddot{y}_C $ to denote the acceleration of the center of mass $C$ in each direction.

$$ \begin{aligned} F_Q &= m\ddot{x}_C \\ F_P - mg &= m\ddot{y}_C \end{aligned} $$

Now we can apply the solution procedure detailed in #rkc-cp to find the acceleration of point $C$. Due to our constraint, the following applies at all times:

$$ x_C = \frac{\ell}{2}\sin\phi \qquad \qquad y_C = \frac{\ell}{2}\cos\phi $$

Differentiating twice, keeping in mind the chain rule:

$$ \begin{aligned} \ddot{x}_C &= -\frac{\ell\dot\theta^2}{2}\sin\phi + \frac{\ell\ddot\theta}{2}\cos\phi \\ \ddot{y}_C &= -\frac{\ell\dot\theta^2}{2}\cos\phi - \frac{\ell\ddot\theta}{2}\sin\phi \end{aligned} $$

Plugging into Newton's second law equations and solving for each constraint force yields:

$$ \begin{aligned} F_Q &= -\frac{m\ell\dot\theta^2}{2}\sin\phi + \frac{m\ell\ddot\theta}{2}\cos\phi \\ F_P &= -\frac{m\ell\dot\theta^2}{2}\cos\phi - \frac{m\ell\ddot\theta}{2}\sin\phi + mg \end{aligned} $$

Example Problem: Instance where rod loses contact with a wall. #rkc-xlc

A uniform rod of mass $m$ and length $\ell$ is leaning against a frictionless wall at rest at an angle $\phi$ as shown. The rod starts sliding on a frictionless ground under the influence of gravity $ \vec{g} $. At what angle $\theta$ does the rod lose contact with the wall?

While there is contact with the wall, our constraint still holds. This means our constraint forces expressions from #rkc-cf still hold. We are only interested in the constraint force from the wall on the rod, $ \vec{F}_Q $. at $ \theta $:

$$ F_Q = -\frac{m\ell\dot\theta^2}{2}\sin\theta + \frac{m\ell\ddot\theta}{2}\cos\theta $$

If the rod loses contact with the wall, then $ \vec{F}_Q = 0 $. We have two unknowns: the angular velocity $\dot\theta$ and the angular acceleration $\ddot\theta$. However, we know that $ \ddot\theta = \frac{d\dot\theta}{dt} $ , so if we obtain an expression for $ \dot\theta $, then finding $ \ddot\theta $ is possible. We can use conservation of energy to obtain an expression for $ \dot\theta $.

Using the work-energy theorem:

$$ W = \Delta T + \Delta V $$

The rod is sliding along frictionless surfaces, so there are no non-conservative forces present, and constraint forces do no work (See work done by a constraint force)

Therefore:

$$ \begin{aligned} T_1 + V_1 &= T_2 + V_2 \\ 0 + mgh_{C, 1} &= \frac{1}{2}mv_C^2 + \frac{1}{2}I_{C, \hat{k}}\omega^2 + mgh_{C, 2} \end{aligned} $$

From before:

$$ \begin{aligned} h_{C, 1} = y_{C, 1} = \ell\cos\phi \qquad h_{C, 2} = y_{C, 2} = \ell\cos\theta \end{aligned} $$

And the velocity of the center of mass at $ \theta $:

$$ \begin{aligned} \vec{v}_C &= \dot{x}_{C,2}\hat{\imath} + \dot{y}_{C, 2}\hat{\jmath} \\ &= \ell\dot\theta\cos\theta \hat{\imath} - \ell\dot\theta\sin\theta \hat{\jmath} \end{aligned} $$

So $ v_C $ is simply $ l\dot\theta $.

Plugging into our energy conservation, where $ I_{C, \hat{k}} = \frac{1}{12}m\ell^2 $:

$$ \begin{aligned} mg\ell\cos\phi &= \frac{1}{2}m(\ell\dot\theta)^2 + \frac{1}{2}\left(\frac{1}{12}m\ell^2 \right) \dot\theta^2 + mg\ell\cos\theta \\ mg\ell\cos\phi &= \frac{1}{2}m\ell^2 \dot\theta^2 + \frac{1}{24}m\ell^2 \dot\theta^2 + mg\ell\cos\theta \\ mg\ell\cos\phi &= \frac{13}{24}m\ell^2 \dot\theta^2 + mg\ell\cos\theta \end{aligned} $$

Solving for $ \dot\theta^2 $ :

$$ \dot\theta^2 = \frac{24g}{13\ell}\left(\cos\phi - \cos\theta\right) $$

Differentiating to obtain $ \ddot\theta $ :

$$ \begin{aligned} 2\dot\theta\ddot\theta &= \frac{24g}{13\ell}\sin\theta\dot\theta \\ \ddot\theta & = \frac{12g}{13\ell}\sin\theta \end{aligned} $$

Plugging our results into $ F_Q $ :

$$ \begin{aligned} F_Q &= -\frac{m\ell\frac{24g}{13\ell}\left(\cos\phi - \cos\theta\right)}{2}\sin\theta + \frac{m\ell\frac{12g}{13\ell}\sin\theta}{2}\cos\theta \\ &= -\frac{12}{13}mg\sin\theta \left(\cos\phi - \cos\theta\right) + \frac{6}{13}mg\cos\theta\sin\theta \\ \end{aligned} $$

Setting $ F_Q=0 $ :

$$ \begin{aligned} \frac{12}{13}mg\sin\theta \left(\cos\phi - \cos\theta\right) &= \frac{6}{13}mg\cos\theta\sin\theta \\ 2\left(\cos\phi - \cos\theta\right) &= \cos\theta \\ 2\cos\phi - 2\cos\theta - \cos\theta &= 0 \\ 2\cos\phi - 3\cos\theta &= 0 \\ \end{aligned} $$

Solving for $ \theta $ yields $ \theta = \arccos\left(\frac{2}{3}\cos\phi\right) $ , or when the rod has fallen 2/3 of the original height. Note if the rod was unconstrained, the constraint we used still holds until the rod has fallen 2/3 of the original height. We can use rigid body relations to find the velocity of point $Q$ once the rod loses contact with the wall, and it will have both vertical and horizontal components of velocity, as expected.

Example Problem: Tension in a compound pulley system. #rkc-xtp

Consider the compound pulley system shown, consisting of two massless pulleys $A, B$. Pulley $A$ is free to move vertically, and pulley $B$ is fixed to the top. The two pulleys are connected by an inextensible, massless rope. One block of mass $m_1$ is connected to pulley $A$ by a string, and another block of mass $m_2$ is hanging from the rope connecting the two pulleys. Assume the pulleys' radii are negligbile, and the rope can only slip. What is the tension $T$ in the rope?

We added one more assumption to the ones made in #rkc-xcp. Namely, the rope can only slip. This simply means that the tension is the same at any point in the rope.

We will begin by drawing a free body diagram and applying Newton's second law on three bodies: $ m_1 $, $ m_2 $ and pulley $A$. We will neglect pulley $B$ as it is fixed to the wall, and the results obtained from it are trivial.

The free body diagram on pulley $A$ is as follows:

Applying Newton's second law:

$$ 2T - T_2 = m_A a_A $$

Since the pulley is massless, that means $ T_2 = 2T $ .

The free body diagram on $ m_1 $ is as follows:

Applying Newton's second law:

$$ 2T - m_1 g = m_1 a_1 $$

Finally, the free body diagram on $ m_2 $ is as follows:

Applying Newton's second law:

$$ T - m_2 g = m_2 a_2 $$

We have 3 unknowns, 2 equations. We apply our constraint equation from #rkc-xcp to relate the accelerations of $ m_1 $ and $ m_2 $:

$$ 2a_1 + a_2 = 0 $$

Solving for $T$ from Newton's second law on $ m_2 $:

$$ T = m_2 a_2 + m_2 g $$

Plugging it into Newton's second law on $ m_1 $:

$$ 2m_2 a_2 + 2m_2 g - m_1 g = m_1 a_1 $$

Since $ a_2 = -2a_1 $ :

$$ \begin{aligned} -4m_2 a_1 + 2m_2 g - m_1g &= m_1 a_1 \\ g\left(2m_2 - m_1 \right) &= a_1\left(m_1 + 4m_2\right) \end{aligned} $$

Solving for $ a_1 $ :

$$ a_1 = \frac{g\left(2m_2 - m_1 \right)}{m_1 + 4m_2} $$

Plugging that result into Newton's second law on $ m_1 $ and solving for $T$:

$$ T = \frac{m_1\frac{g\left(2m_2 - m_1 \right)}{m_1 + 4m_2} + m_1g}{2} $$

Simplifying a little by multiplying the top and bottom by $ m_1 + 4m_2 $ :

$$ T = \frac{m_1g(2m_2 - m_1) + m_1g(m_1 + 4m_2)}{2(m_1 + 4m_2)} $$

We obtain our final result for the tension in the rope $T$:

$$ T = \frac{3m_1m_2g}{m_1 + 4m_2} $$

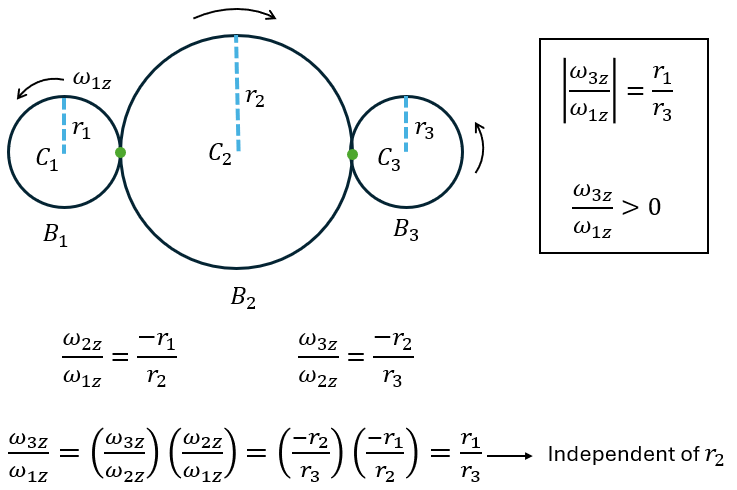
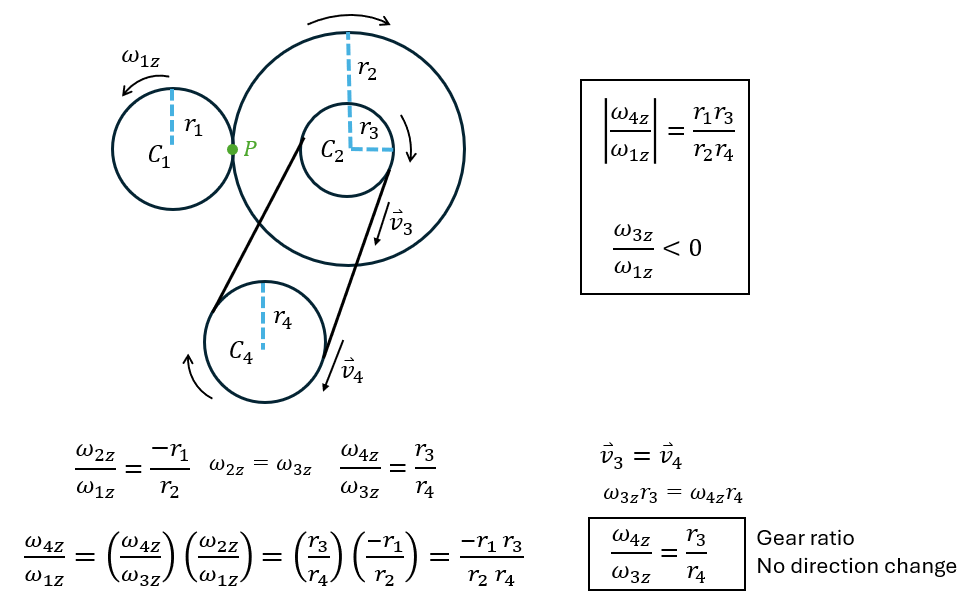
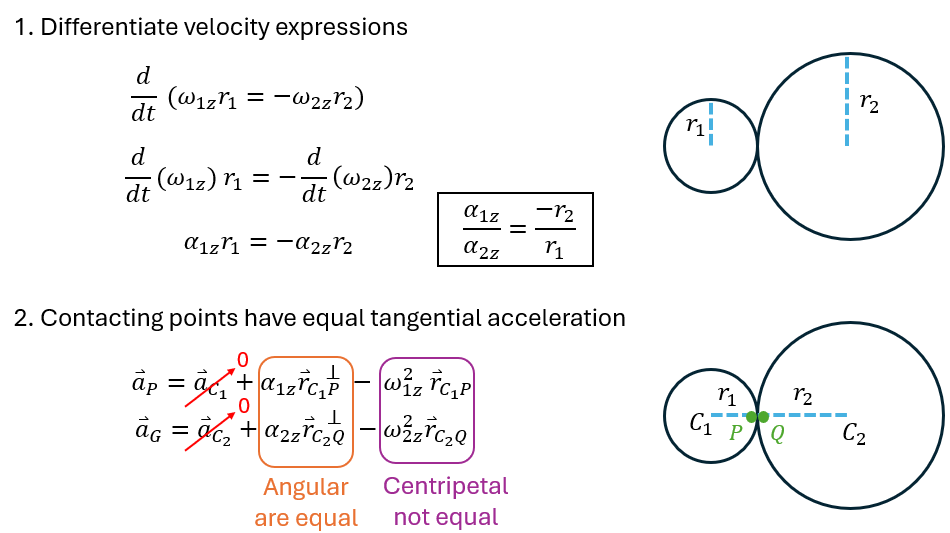
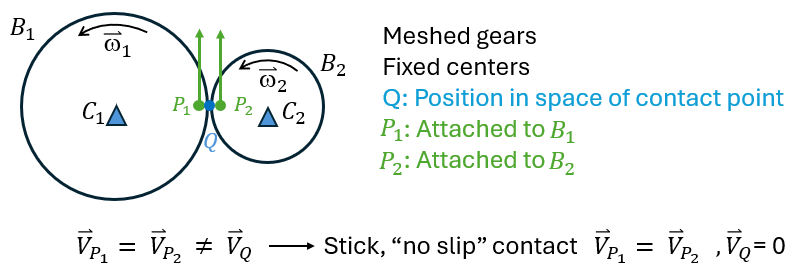
Gears

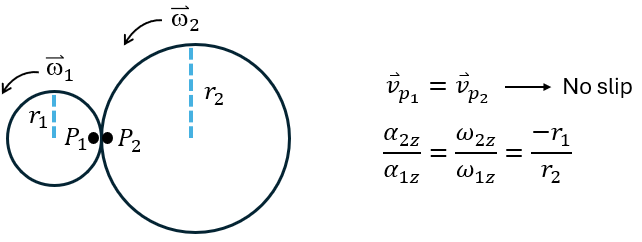
Larger gear - > slower spin
Accelerations - > tangential are equal but centripetal are not
Opposite direction

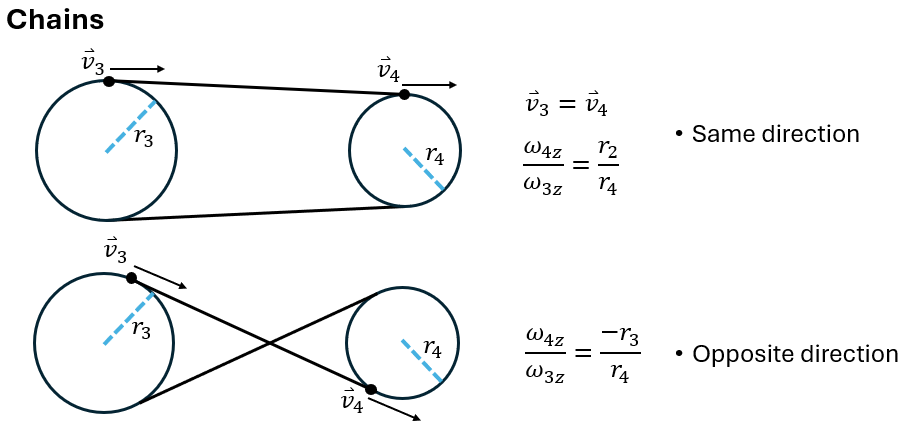
Standard sign convention

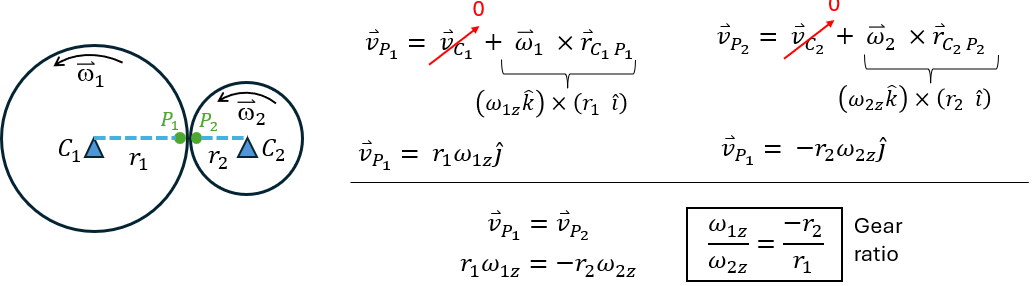
$ \omega_{1z} $ and $ \omega_{2z} $ have opposite signs (the gears rotate in opposite direction)
Smaller gears rotate faster

Example: Rotating gears. #rkc-gsc

Example: Rotating gears with chain. #rkc-csc

Acceleration in contact (no slip)

Applications

Steering geometry

We are all familiar with the idea that turning the steering wheel in a car rotates the front wheels, causing the car to steer into a turn. But why do we normally steer with the front wheels rather than the rear wheels (or all four wheels, as shown below)? Do both front wheels turn the same amount, or is something more complicated going on?

A Mercedes-Benz Typ G 5 (W 152, 1937–1941) housed in Technik Museum Speyer, showing the use of a four-wheel steering system. Image source: Wikimedia Commons (CC BY-SA 3.0) (full-sized image).

Reference material

Rigid bodies

Constrained motion

Turning rigid bodies

When a rigid body turns in a circle, the four corners of the body all move with different velocities and speeds. If we think of a car as a single rigid body with wheels at the corners, this means the four wheels move with different speeds and also different directions. Car designers can choose different steering arrangements, as shown below, where the steering can be with the front two wheels only (conventional cars), with the rear two wheels only (forklifts), or with all four wheels in some high-performance cars.

Show:

Turn radius:

$r = \; $ 5m

Vehicle offset:

$d = \; $ 0%

A car turning in a circle, showing the directions that the wheels must point as the turn radius $r$ and offset $d$ change.

Did you know?

Forklifts typically have fixed front wheels and steer with the rear wheels. This gives them great control over the position of the front lifting forks, but makes steering harder for the operator. Rear-wheel steering is a type of non-minimum phase control system. The technical definition of minimum phase is somewhat complicated, but for vehicle steering it essentially means that we have to steer the “wrong way”. For example, to turn right in a forklift we have to first swing the back out to the left. This makes it very easy to accidentally run into obstacles, and is also unstable at higher speeds.

A Yale GLP-50VX forklift executing a sharp right-hand turn. Image credit: Flickr image by Anastasia Victor (CC BY 2.0) (full-sized image).

Sometimes in cars it would be convenient to also steer with the rear or trailing wheels, for example when trying to park in a tight spot. We actually have a mechanism for converting a car to trailing-wheel steering, which is to drive backwards, such as when parallel parking.

Ackerman steering geometry

In a conventional car, the rear two wheels are fixed to point straight ahead, while the front two wheels must turn at different but matched angles. To achieve the correct front wheel angles, cars typically use a four-bar linkage as shown below. The pins at $A$ and $B$ are called kingpins (normally actually ball joints in modern cars), the $CD$ rod is called the tie rod, and the $AD$ and $BC$ rods are called steering arms. By correctly choosing the lengths of the linkage rods, the car steering will automatically produce nearly correctly matched front wheel angles to make a perfect turn with any radius of curvature.

Steering pivot offset angle:

$\theta = \; $ 0$^\circ$

Adjustable Ackerman steering geometry. The graph shows the radius of curvature for the two front wheels as a function of the rack offset $d$.

Did you know?

Three wheeled vehicles with two wheels in back and one in front (a delta or tricycle configuration) avoid the need for complicated steering geometry, leading Karl Benz to use this system in the world's first automobile.

Benz Patent-Motorwagen Nr. 3 from 1888. Image credit: Wikimedia Commons (public domain) (full-sized image).

Episode 4 of Season 9 of Top Gear featured a segment on the Reliant Robin, a three-wheel car produced in the 1970s in the United Kingdom. This Top Gear episode clearly demonstrates some of the reasons that single-wheel steering systems for cars have not achieved long-lasting commercial success.

Three-wheeled cars were rather popular with British manufacturers in the 1960s and 1970s. As well as single-wheel-in-front models like the Reliant Robin, there were also production cars with a single wheel in the back (a tadpole configuration). An example of this is the smallest production car ever made, the Peel 50, shown in another Top Gear episode (Series 10, Episode 3).

Knee Joint

The human knee joint is a type of biological hinge, which allows movement in only one primary angle. The knee connects the femur (the upper leg bone) to the tibia (the larger of the two lower leg bones). These two bones sit next to each other and are free to rotate about a single axis. A mechanism is needed to keep the two legs bones attached to each other, while still allowing rotation. In the case of the human knee this is achieved with a four-bar linkage consisting of the two bones together with the anterior cruciate ligament (ACL) and posterior cruciate ligament (PCL), as shown below.

An MRI image of a sagittal section through a human knee joint, showing the ACL and PCL ligaments. Image credit: Wikimedia Commons image (CC BY-SA 2.0).

The four-bar model of the knee is only approximate, and neglects many important mechanical features. In particular, the ACL and PCL are not rigid rods, and can only provide tensile forces (they act as mechanical ropes). The compressive force is actually provided by the meniscus that separates the femur and tibia bones. In the simple four-bar knee model shown here, the rigid rods include the effects of both the ligaments and the meniscus.

References

A. B. Zavatsky and J. J. O'Connor. A model of human knee ligaments in the sagittal plane: Part 1: Response to passive flexion. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine, 206(3):125–134, 1992. DOI: 10.1243/PIME_PROC_1992_206_280_02

Did you know?

No joints in the human body have the rotating bone fully constrained by the enclosing socket bone. Instead, like the knee, they have a partial socket or cylinder and the rotating bone is held in place by ligaments. This type of arrangement is typical for most animals, with one rare exception being the European Badger (Meles Meles). In older badgers, the jaw rotates on an entirely enclosed pivot, as shown below. This means that the badger cannot waggle its jaw side-to-side as humans can, and also means that the badger jaw cannot be dislocated or disconnected without breaking the bone.

Image credit: Wikimedia Commons (CC BY-SA 3.0) (full-sized image).

Suspensions with Watt's linkage

Apart from being one of the inventors of the steam engine and having an SI unit named after him, James Watt also developed a linkage to produce approximate straight line motion. Watt's linkage consists of two long near-parallel links and a small floating link between them, with the near-linear motion occurring for a coupler point midway along the floating link. This linkage is commonly used in suspension systems, as shown below.

The rear suspension of a 1998 Ford Ranger EV. Image credit: Wikimedia Commons (CC SA 1.0) (full-sized image).

	location description	velocity description
point mass	position vector \( \vec{r}_P \)	velocity vector \( \vec{v}_P \)
rigid body in 2D	position vector \( \vec{r}_P \) angle \(\theta\)	velocity vector \( \vec{v}_P \) angular velocity \( \omega \)
rigid body in 3D	position vector \( \vec{r}_P \) angles \( \theta,\phi,\psi \)	velocity vector \( \vec{v}_P \) angular velocity vector \( \vec{\omega} \)

Movement:	translation	var. translation	rotation	var. rotation	slide
	hinge	circle	spin	reverse spin	oscillation

Rigid bodies

Rotating rigid bodies

Points on rigid bodies

Rigid bodies in 2D

Constrained motion

Constraint forces

Gears

Standard sign convention

Acceleration in contact (no slip)

Applications

Steering geometry

Turning rigid bodies

Ackerman steering geometry

Knee Joint

References

Suspensions with Watt's linkage

Learn More